Навигация
Получение случайных чисел
Овладение навыками алгоритмизации и программирования задач с использованием датчиков случайных чисел, способами получения случайных чисел с различными законами распределения, навыками оценки качества псевдослучайных чисел и их соответствия заданному закону распределения.
1.2. Задания для самостоятельной подготовки
Изучить:
способы получения случайных чисел с различными законами распределения;
-способы использования в программах обращений к функциям или подпрограммам для получения псевдослучайных чисел с различными законами распределения;
способами использования случайных чисел для моделирования.
Разработать алгоритм решения в соответствии с заданием.
Составить программу решения задачи.
Подготовить тестовый вариант программы и исходных данных.
1.3. Задание к работе
1. Выполнить на ЭВМ программу в соответствии со следующим заданием:
Сгенерировать последовательность из 50 случайных чисел с нормальным законом распределения а=5,s =4) и последовательность из 50 случайных чисел с экспоненциальным законом распределения с параметром l =5. Все числа свести в массив, расположив их по возрастанию. Вычислить среднее значение, дисперсию и вывести результаты на печать в виде гистограммы, разбив последовательность чисел на десять интервалов
2. Проверить правильность выполнения программы с помощью тестового варианта.
2. Руководство программиста.
Прежде, чем приступить к самому процессу алгоритмизации и программирования заглянем в теорию, по которой, собственно, и дано задание.
2.1. Теоретическая база.
2.1.1. Нормальное распределение.
Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
![]()
Мы видим, что нормальное распределение определяется двумя параметрами: а и s . Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, вероятностный смысл этих параметров таков: а есть математическое ожидание, s —среднее квадратическое отклонение нормального распределения.
2.1.2 Показательное (экспоненциальное) распределение.
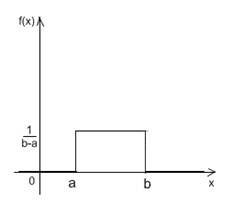
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью
![]()
где l - постоянная положительная величина.
Мы видим, что показательное распределение определяется одним параметром l . Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два или три и т. д. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.
2.2. Начало алгоритмизации.
Для получения двух последовательностей из 50 случайных чисел с показательным и нормальным законами распределения необходимо организовать цикл, который будет выполнятся 50 раз. Внутри цикла будем пользоваться функцией из Турбо Паскаля random(a) - эта функция выдает произвольное число из интервала от 1 до a, a£ 65535. Каждое полученное число будет вносится в массив, причем первые 50 элементов этого массива получены по нормальному закону, а другие 50 - по показательному.
Для упорядочивания массива случайных величин создадим двойной цикл. Для расчета мат. ожидания и дисперсии упорядоченного массива также создадим двойной цикл, с учетом того, что массив уже надо разбить на 10 частей и расчет проводить по каждому из промежутков. Для построения гистограммы воспользуемся средствами модуля Graph.tpu.
Блок-схемой основной программы будет приведена в приложении. Также в приложении будут размещены блок-схемы подпрограмм-процедур, используемых в данной программе.
Перед процессом программирования составим таблицу используемых в программе и подпрограммах таблицу переменных и констант.
Таблица 1. Описание переменных и констант.
| Имя переменной | Назначение | Тип в Turbo Pascal |
| i.j | Переменные циклов. | Byte |
| help,work,button | Переменный для хранения параметров вызова процедур. | Byte |
| actionprog,action | Символьные переменные для управления интерфейсной частью .основной программы и процедур соответственно. | Char |
| exitpar,exitmenu,exitprog | Логические параметры, задающие выход из процедур и основной программы. Позволяют делать программу более гибкой в применении. | Boolean |
| grmode,grdriver | Переменные, содержащие данные о типе графического драйвера и его режиме работы. Установлены в программе на автоматическое определение. | Integer |
| Dat(3) | Массив для хранения входных данных в программе. Начальное значение [5,4,5]. | array[1..3]of real |
| Posle(100) | Массив для хранения элементов генерируемой последовательности. | array[1..100] of real |
| Xcor(3),Ycor(3) | Массивы, используемые для более компактности ввода параметров генерации последовательности в процедуре DoWorkс параметром work=1. | array[1..3]of byte |
| Mat(10),Disp(10) | Массивы с данными о дисперсии и мат.ожидании по промежуткам последовательности. | array[1..10]of real |
| mat0,disp0 | Мат.ожидание и дисперсия по всей последовательности. | Real |
| X | Временная переменная (буфер). | Real |
| Col(4) | Массив для управления выбора пункта меню. | array[1..4]of byte |
| Light.Dark | Константы для задания цветов меню. | [1..16] |
Похожие работы
... получаются экспериментальная и теоретическая зависимости P (j, l), сходимость которых проверяется по известным критериям, причем проверку целесообразно проводить при разных значениях l и р, 0 < р < 1. 7. Генератор случайных чисел в Borland C++ В языке C, как и во многих других языках высокого уровня, существует встроенная поддержка генератора случайных чисел. Для формирования чисел ...
... ;…≤ξn . Шаг 3. Нужные статистики вычисляются по формулам Kn+ = max ( - F(xj)); Kn- -= max (F(xj) - ), при 1≤j≤n. Заключение В данной курсовой работе рассмотрены вопросы применения случайных чисел для прикладных задач математики и информатики, рассмотрены методы получения случайных чисел, начиная от самых ранних методов с использованием первых вычислительных машин ...
... величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.2.2. Начало алгоритмизации. Для получения двух последовательностей из 50 случайных чисел с показательным и нормальным законами распределения необходимо организовать цикл, который будет выполнятся 50 раз. Внутри цикла будем пользоваться функцией из Турбо Паскаля ...
... нельзя в полной мере назвать случайными, поскольку между ними имеется зависимость, а также наличие периодов в последовательности псевдослучайных чисел. К алгоритмическим методам получения ГСЧ относиться метод серединных квадратов, предложенный в 1946 г. Дж. фон Нейманом. Метод серединных квадратов Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее ...
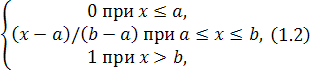
0 комментариев