Навигация
2.3.5. Процедура drawmenu.
Быстрый вызов – F10.
Можно сказать, что весь интерфейс программы, ее простота использования во многом зависит от грамотно созданного меню. Некое подобие меню как раз возложено на создание этой процедуры.
Алгоритм процедуры полностью замешен на символьных данных, используемых в качестве кодов “горячих” клавиш и клавиш скроллинга. Для визуализации выбора пункта меню используется выделение цветом того или иного пункта меню. Все цвета меню можно зажать путем изменения значений констант light и dark – соответственно активного и неактивного пункта меню. Подобный ход можно использовать в подборе цветов, удобных для пользователя.
Предусмотрен первоначальный вывод меню без выбора какого-нибудь из пунктов. Это необходимо для прорисовки интерфейса в начале работы программы и после просмотра гистограммы.
При выборе любого из пунктов меню происходит вызов процедуры drawhelp со значением 1-4 в зависимости от того какой пункт был выбран. Значение 1 предано крайнему левому пункту, 4 – правому. Подробнее о текстах справки можно посмотреть в таблице 3.
Как и во многих программах можно избежать входа в меню – для выбора любого пункта назначена “горячая” клавиша. Информация об этом выдается при запуске программы.
3. Руководство пользователя.
Этот раздел предназначен для пояснения как общаться с программой.
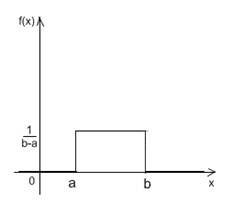
Данная программа предназначена для построения гистограммы последовательности чисел полученной по двум законам распределения – нормальному и экспоненциальному. При выводе используется графический режим. Перед выводом последовательность разбивается на 10 интервалов и демонстрацией результата является мат.ожидание и дисперсия для каждого из интервалов.
В программе предусмотрена строка помощи для пользователя, в которой описаны быстрый клавиши вызова того или иного пункта возможных действий. Все возможные подсказки можно просмотреть в таблице 3 в разделе “Руководство программиста”.
При запуске формируется окно с разделением на три области: меню, диалоговую часть и строку помощи. При выборе любого из пункта меню происходит вызов определенной части программы, а также смена интерфейса.
При выборе пункта “Параметры” пользователю будет предложено окно, в котором можно будет задать параметры для генерации последовательности. В правой колонке для нормального закон, в левой – для экспоненциальной. Чтобы изменить параметр необходимо нажать BckSp (Забой), после чего становится возможным изменение параметра. Переключение между параметрами осуществляется через клавишу Tab или Enter. Также переход происходит автоматически после изменения параметра. В этом же пункте меню происходит генерация последовательности – клавиша F4. Выход из этого режима осуществляется через клавишу Escape.
Пункт “Последовательности” позволяет осуществить просмотр уже существующей последовательности. Чтобы просмотреть всю последовательность целиком воспользуйтесь клавишами скроллинга (прокрутки) Up/Down. Выход из режима – Escape.
Просмотр гистограммы производится при выборе одноименного пункта. Гистограмма имеет легенду. Выходом из просмотра является нажатие на любую клавишу.
Для выхода можно воспользоваться комбинацией клавиш Alt-x или же через меню.
Таблица 4. Комбинации “горячих” клавиш программы.
| Комбинация | Действие (вход в режим) | |
| Начальный режим | ||
| F1 | Параметры | |
| F2 | Последовательности | |
| F3 | Гистограмма | |
| F10 | Вход в меню | |
| Alt-x | Быстрый выход | |
| Параметры | ||
| Enter | Закончить изменение параметра | |
| Escape | Выход из режима | |
| Tab | Переключится на следующий параметр | |
| F4 | Построить последовательность | |
| Последовательности | ||
| Up/Down | Просмотр вверх/вниз последовательности | |
| Escape | Выход из режима | |
| Гистограмма | ||
| Любая клавиша | Выход из режима | |
4. Заключение.
Научились применять математический аппарат при программировании на Turbo Pascal. Написали программу используя все знания полученные по курсу “Информатика”. Вникли в понятие интерфейса и сделали попытку в разработке собственного дизайна программы.
program kursovik;
uses crt,graph;
var j,help,i,work,button:byte;
exitmenu,exitprog:boolean;
actionprog,action:char;
grmode,grdriver:integer;
dat:array[1..3]of real;
posle:array[1..100] of real;
xcor,ycor:array[1..3]of byte;
mat,disp:array[1..10]of real;
mat0,disp0,dispmax,matmax,x:real;
{*****DrawHelp*****}
procedure drawhelp(help:byte);
begin
textcolor(black);
textbackground(white);
gotoxy(1,25);
case help of
0: write(' F1-Парам. F2-Посл-ти F3-Гистогр. F10-Меню (Alt-x)-Выход ');
1: write(' Задать/изменить параметры ');
2: write(' Просмотреть последовательности ');
3: write(' Просмотреть гистограмму ');
4: write(' Выход ');
5: write(' Esc-Закончить изменение параметров. BckSp-Изменить параметр. F4-Постр. посл-ть');
6: write(' Нажмите Up или Down для просмотра или Esc для выхода ');
end;
end;
{*****DrawWin*****}
procedure drawwin;
begin
textcolor(white);textbackground(blue);
GotoXY(1,2);
Write('г');
for i:=2 to 79 do
Write('=');
Write('¬');
for i:=3 to 23 do
begin
GotoXY(1,i1);
Write('¦');
for j:=2 to 79 do
Write(' ');
Write('¦');
end;
GotoXY(1,24);
Write('L');
for i:=2 to 79 do
Write('=');
Write('-');
{ gotoxy(39,2);write('T');}
gotoxy(39,24);write('¦');
for i:=5 to 23 do
begin
gotoxy(39,i);
write('¦')
end;
gotoxy(31,3);
writeln('Последовательности');
gotoxy(1,4);
write('¦=====================================T========================================¦');
end;
{*****DoWork*****}
procedure dowork(work:byte);
begin
case work of
1: begin
textcolor(white);
textbackground(blue);
gotoxy(39,2);write('T');
gotoxy(2,3);
writeln(' Нормальный закон: ¦ Экспоненциальный закон:');
gotoxy(1,4);
write('¦=====================================+========================================¦');
drawhelp(5);
textcolor(white);
textbackground(blue);
gotoxy(2,6);write(' Мат. ожидание:');
gotoxy(2,8);write(' Дисперсия:');gotoxy(xcor[2],ycor[2]);write(dat[2]:2:1);
gotoxy(41,6);write('Коэффициент:');gotoxy(xcor[3],ycor[3]);write(dat[3]:2:1);
gotoxy(xcor[1],ycor[1]);write(dat[1]:2:1);i:=1;
repeat
action:=readkey;
case action of
#27: exitpar:=true;
#9: begin
i:=i+1;
if i<4 then
begin
gotoxy(xcor[i],ycor[i]);write(dat[i]:2:1);
end
else
begin
i:=1;
gotoxy(xcor[1],ycor[1]);write(dat[1]:2:1);
end;
end;
#8: begin
gotoxy(xcor[i],ycor[i]);write(' ');
gotoxy(xcor[i],ycor[i]);read(dat[i]);
gotoxy(xcor[i],ycor[i]);write(dat[i]:2:1);
if i<3 then i:=i+1 else i:=1;
gotoxy(xcor[i],ycor[i]);write(dat[i]:2:1);
end;
#13: begin
if i<3 then i:=i+1 else i:=1;
gotoxy(xcor[i],ycor[i]);write(dat[i]:2:1);
end;
#62: begin
for i:=1 to 50 do
begin
x:=ln(random(65525)+1);
posle[i]:=exp(-sqr(x-dat[1])/(2*sqrt(dat[2])))/sqrt(2*pi*dat[2]);
x:=exp(1/(random(825)));
if x<0 then posle[i+50]:=0 else posle[i+50]:=dat[3]*exp(-dat[3]*x);
end;
end;
end;
until exitpar=true;
drawwin;
end;
2: begin
action:=#1;
drawhelp(6);
textcolor(white);
textbackground(blue);
exitpar:=false;
j:=1;
for i:=1 to 19 do
begin
gotoxy(2,i+4);
if i+j-1<10 then write(' ',i+j-1,': ',posle[i+j]:2:6,' ¦ ',i+j+49,': ',posle[i+50+j]:2:6)
else write(' ',i+j-1,': ',posle[i+j]:2:6,' ¦ ',i+j+49,': ',posle[i+50+j]:2:6)
end;
repeat
action:=readkey;
case action of
#72: if j>1 then j:=j-1;
#80: if j<32 then j:=j+1;
#27: exitpar:=true;
end;
for i:=1 to 19 do
begin
gotoxy(2,i+4);
if i+j-1<10 then write(' ',i+j-1,': ',posle[i+j]:2:6,' ¦ ',i+j+49,': ',posle[i+50+j]:2:6)
else write(' ',i+j-1,': ',posle[i+j]:2:6,' ¦ ',i+j+49,': ',posle[i+50+j]:2:6)
end;
until exitpar=true;
drawwin;
end;
3: begin
for i:=1 to 10 do
begin
x:=0;
for j:=1 to 10 do
x:=x+posle[(i-1)*10+j];
mat[i]:=x/10;
mat0:=mat0+x;
end;
mat0:=mat0/100;
for i:=1 to 10 do
for j:=1 to 10 do
begin
disp[i]:=sqr(posle[(i-1)*10+j]-mat[i]);
disp0:=sqr(posle[(i-1)*10+j]-mat0);
end;
matmax:=mat[1];
dispmax:=disp[1];
for i:=1 to 10 do
begin
if disp[i]>dispmax then dispmax:=disp[i];
if mat[i]>matmax then matmax:=mat[i];
end;
initgraph(grdriver,grmode,'');
setBKcolor(black);setcolor(8);
for i:=1 to 11 do
line(5,i*30,15,i*30-10);
for i:=1 to 20 do
line(i*25+5,330,i*25+15,320);
line(5,330,505,330);
line(5,330,5,30);
for i:=0 to 20 do line(i*25+15,320,i*25+15,20);
for i:=1 to 11 do line(15,i*30-10,515,i*30-10);
setbkcolor(black);
for i:=1 to 10 do
begin
setcolor(cyan);
SetFillStyle(6, 7);
Bar3D(13,27+30*(i-1),13+round(mat[i]*10000),35+30*(i-1), 2, TopOn);
setcolor(green);
SetFillStyle(8, 8);
Bar3D(13,35+30*(i-1),13+round(disp[i]*1000000),43+30*(i-1), 2, TopOn);
end;
SetFillStyle(6, 7);
setcolor(8);
bar(10, 430, 20, 440);
outtextxy(23,432,'- Mat. ozhidanie');
SetFillStyle(8, 8);
bar(10, 450, 20, 460);
outtextxy(23,452,'- Dispersiya');
readkey;
closegraph;
drawwin
end;
end;
end;
{*****DrawMenu*****}
procedure drawmenu(button:byte);
const light=green;{15,14,13,12,11,10,9}
dark=white;{7,6,5,4,3,2,1}
var col:array[1..4]of byte;
exitmenu:boolean;
begin
exitmenu:=false;
textcolor(black);
drawhelp(1);
repeat
for i:=1 to 5 do col[i]:=dark;
col[button]:=light;
gotoxy(1,1);
textbackground(col[1]);write(' Параметры ');
textbackground(col[2]);write(' Последовательности ');
textbackground(col[3]);write(' Гистограмма ');
textbackground(col[4]);write(' Выход ');textbackground(dark);write(' ');
if button<>5 then action:=readkey else exitmenu:=true;
case action of
#77: begin
if button<4 then
begin
col[button]:=dark;
button:=button+1;
col[button]:=light
end
else
begin
col[4]:=dark;
col[1]:=light;
button:=1;
end;
end;
#75: begin
if button>1 then
begin
col[button]:=dark;
button:=button-1;
col[button]:=light
end
else
begin
col[1]:=dark;
col[4]:=light;
button:=4;
end
end;
#27: exitmenu:=true;
#13: case button of
1: begin
dowork(1);
button:=5
end;
2: begin
dowork(2);
button:=5
end;
3: begin
dowork(3);
button:=5
end;
4: begin
exitmenu:=true;
exitprog:=true
end;
end;
end;
if button<>5 then drawhelp(button);
until exitmenu=true;
drawhelp(0);textbackground(dark);gotoxy(1,1);
write(' Параметры Последовательности Гистограмма Выход ');
end;
{*****Главная программа*****}
begin
clrscr;
xcor[1]:=18;
xcor[2]:=18;
xcor[3]:=58;
ycor[1]:=6;
ycor[2]:=8;
ycor[3]:=6;
dat[1]:=5;dat[3]:=5;dat[2]:=4;
grmode:=detect;
grdriver:=detect;
drawwin;
repeat
drawmenu(5);
drawhelp(0);
actionprog:=readkey;
case actionprog of
#59: dowork(1);
#60: dowork(2);
#61: dowork(3);
#68: begin
drawmenu(1);
end;
#45: exitprog:=true;
end;
for i:=1 to 10 do begin mat[i]:=0; disp[i]:=0 end;
until exitprog=true;
end.
Похожие работы
... получаются экспериментальная и теоретическая зависимости P (j, l), сходимость которых проверяется по известным критериям, причем проверку целесообразно проводить при разных значениях l и р, 0 < р < 1. 7. Генератор случайных чисел в Borland C++ В языке C, как и во многих других языках высокого уровня, существует встроенная поддержка генератора случайных чисел. Для формирования чисел ...
... ;…≤ξn . Шаг 3. Нужные статистики вычисляются по формулам Kn+ = max ( - F(xj)); Kn- -= max (F(xj) - ), при 1≤j≤n. Заключение В данной курсовой работе рассмотрены вопросы применения случайных чисел для прикладных задач математики и информатики, рассмотрены методы получения случайных чисел, начиная от самых ранних методов с использованием первых вычислительных машин ...
... величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.2.2. Начало алгоритмизации. Для получения двух последовательностей из 50 случайных чисел с показательным и нормальным законами распределения необходимо организовать цикл, который будет выполнятся 50 раз. Внутри цикла будем пользоваться функцией из Турбо Паскаля ...
... нельзя в полной мере назвать случайными, поскольку между ними имеется зависимость, а также наличие периодов в последовательности псевдослучайных чисел. К алгоритмическим методам получения ГСЧ относиться метод серединных квадратов, предложенный в 1946 г. Дж. фон Нейманом. Метод серединных квадратов Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее ...
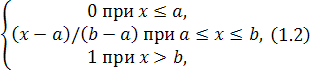
0 комментариев