Навигация
Квантование сигналов по времени
15480
знаков
0
таблиц
7
изображений
Курсовой проект по дисциплине «Теория информации и сигналов»
Выполнила студентка группы 03-КТ-11 курса 3 факультета КТАС
Кубанский Государственный технологический университет
Кафедра ВТ и АСУ
Краснодар, 2005
Введение
В настоящее время информация стала фактором, определяющим эффективность любой сферы деятельности. Увеличились информационные потоки и повысились требования к скорости передачи данных, одним из факторов повышения скорости передачи данных служит метод дискретизации сигналов по времени, т.е. при передачи сигнала, можно передавать не весь сигнал, а только его отчеты, и восстанавливать сигнал по отчетам. В этом случае передаются только импульсы (щелчки), а на приемнике, по этим щелчкам восстанавливается сигнал
В работе реализуется алгоритм квантования сигналов по времени.
1. Классификация видов модуляции
Сообщение, представленное электрическим сигналом, должно быть передано на определенное расстояние (в том числе на достаточно большое). Для этой цели используются сигналы - переносчики. Энергия переносчиков должна быть достаточной для передачи на заданное расстояние.
Таким образом, преобразование сигналов при передаче состоит в воздействии на переносчик, изменяющем тот или иной его параметр. Это воздействие называется модуляцией.
Различные виды модуляции характеризуются различными видами переносчиков, а так же рядом параметров, подвергаемых изменению.
По виду переносчиков различают:
модуляцию синусоидальных (гармонических) сигналов;
модуляцию импульсных сигналов.
По изменяемым параметрам различают:
амплитудную модуляцию;
частотную модуляцию;
фазовую модуляцию;
кодовую модуляцию и др.
В тех случаях, когда непрерывное сообщение передается в дискретной (цифровой) форме, осуществляется предварительное преобразование непрерывного сообщения в дискретное, включающее дискретизацию (квантование) по времени и по уровню.
2. Модуляция импульсных переносчиков
В новейших системах передачи информации, в особенности в многоканальных системах с временным уплотнением (разделением) каналов, переносчиком является последовательность прямоугольных импульсов. У такого переносчика можно изменять следующие параметры: амплитуду импульсов, их ширину, частоту следования, позицию или фазу и коды, образуемые ими. Соответственно различают следующие модуляции:
амплитудно-импульсная модуляция АИМ;
широтно-импульсная модуляция ШИМ;
время-импульсная модуляция ВИМ;
позиционно-импульсная модуляция (фазо-импульсная) ПИМ (ФИМ);
частотно-импульсная модуляция ЧИМ;
кодо-импульсная модуляция КИМ.
При передаче непрерывных сообщений в информационных системах весьма широкое применение получила кодоимпульсная модуляция (КИМ) сигналов. КИМ складывается из трех операций:
дискретизации сигналов по времени;
дискретизации сигналов по уровню;
кодирования.
Дискретизация по времени заключается в замене непрерывного по времени сигнала X(t) дискретным сигналом, значения которого для дискретных моментов времени t совпадают соответственно с мгновенными значениями непрерывного сигнала. Такая операция называется также квантованием сигнала по времени.
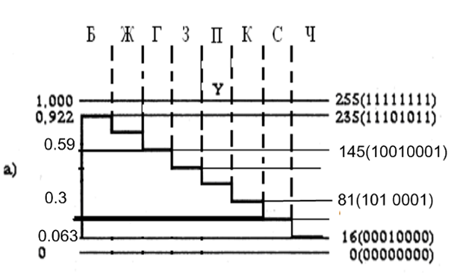
Дискретизация по уровню (квантование по уровню) заключается в замене непрерывного множества значений сигнала X(t) множеством дискретных значений. При этом шкала возможных значений сигнала разбивается на определенное количество интервалов и непрерывное значение сигнала заменяется ближайшим дискретным. Полученные дискретные значения затем кодируются (обычно двоичным кодом).
КИМ (кодо-импульсная модуляция) обеспечивает существенное повышение помехоустойчивости передачи сообщений. Кроме того, дискретизация по времени позволяет использовать одни и те же устройства (каналы связи, устройства обработки информации и пр.) для большого числа различных сигналов.
При КИМ весьма важным является правильный выбор способа квантования сигнала по времени и уровню. В связи с этим рассмотрим некоторые вопросы теории квантования непрерывных функций по времени и уровню.
3. Квантование сигналов по времени
3.1 Определение дискретизации сигналов по времени
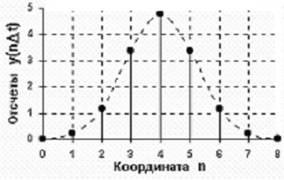
При квантовании по времени непрерывная по аргументу функция x(t) преобразуется в функцию 
дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции x(t) в определенные дискретные моменты времени 
. В результате функция x(t) заменяется совокупностью мгновенных значений x(ti) [i=0,1,2,…,n].
Временной интервал 
между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется интервалом временного квантования. Величина, обратная интервалу временного квантования
называется частотой квантования.
Частота квантования должна выбираться таким образом, чтобы по отсчетным значениям x(ti) можно было бы с заданной точностью получить исходную функцию.
Похожие работы
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
... ИКМ сигнала на приемной станции; ПК пр – преобразователь кода – преобразует биполярный сигнал в однополярный; Пр СС – приемник синхросигналов – правильное декодирование и распределение сигналов по своим телефонным каналам и каналам передачи СУВ; УР – устройство разделения – разделяет кодовые группы ТЛФ каналов и СУВ; Пр СУВ – приемник групповых сигналов управления и взаимодействия – ...
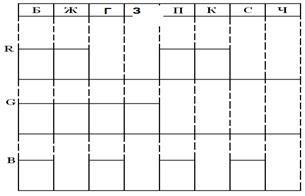
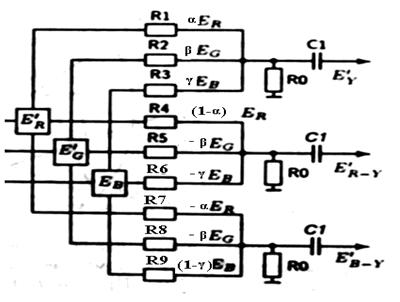
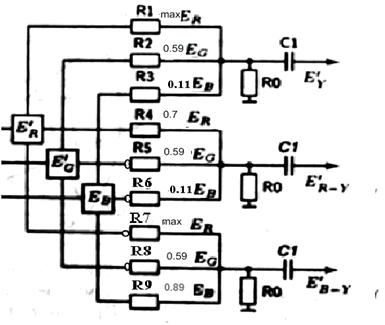
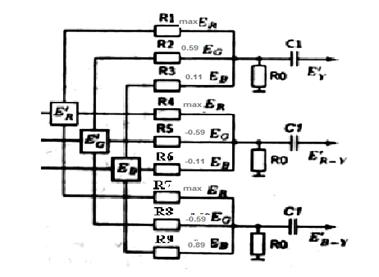
... соответствует нулевому значению цветоразностного сигнала. При воспроизведении пурпурного цвета E'B-Y = 0.59, т. е.: CB=126·E'B-Y+128=202=11001010 При воспроизведении голубого цвета E'B-Y =0.3, т. е.: CB=126·E'B-Y+128=165.8=10100101 3. Графики изменения сигналов яркости и цветности во времени в строчном периоде для текстового изображения «градационный клин» Рисунок 5. Графики ...
... нельзя проводить отбор отдельных компонентов ИС по допуска, как это имело место в схемах дискретных электорадиоэлементах в ЭВМ третьего поколения. Разработка генератора на цифровых микросхемах. Для проверки и настройки цифровых интегральных микросхемах транзисторно-транзисторной логики (ТТЛ) требуются генераторы прямоугольных импульсов. Ниже описывается генератор импульсов, выполненный всего на ...
0 комментариев