Навигация
Выбор шага квантования по времени
3.2 Выбор шага квантования по времени
Известно несколько критериев выбора частоты квантования по времени. К таким критериям относится, в частности, частотный критерий В.А. Котельникова. Данный критерий, который получил название теоремы В.А. Котельникова, основывается на следующей модели сигналов:
сигнал представляет собой стационарный случайный процесс;
спектр сигнала сплошной и ограничен некоторой частотой, за пределами которой он тождественно равен нулю.
Теорема В.А. Котельникова: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число экстремумов) и ее спектр ограничен некоторой частотой fc, то она полностью определяется отсчетами, находящимися на расстоянии ![]() друг от друга.
друг от друга.
Для доказательства теоремы рассмотрим выражения прямого и обратного преобразования Фурье непрерывной функции x(t).
![]() (1)
(1)
![]() . (2)
. (2)
В рассматриваемом частном случае функции с ограниченным спектром можно записать
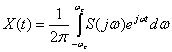 . (3)
. (3)
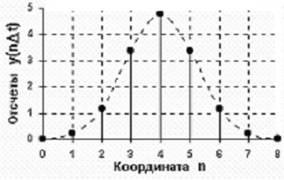
Дополним функцию до периодической с периодом, равным 2fc (рисунок 1) и разложим ее в ряд Фурье
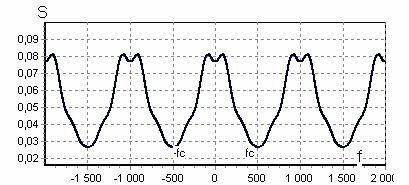
Рисунок 1 - функция с периодом, равным 2fc.
![]() , (4)
, (4)
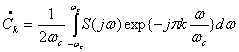 . (5)
. (5)
Сравнивая выражения (3) и (5) замечаем, что они совпадают с точностью до постоянного множителя ![]() , если принять
, если принять ![]() .
.
Следовательно,
![]() .
.
Подставив найденное выражение для ![]() в (4), получим
в (4), получим
![]() . (6)
. (6)
После подставки (6) в (3), замены знака при k (т.к. суммирование производится по всем положительным и отрицательным значениям k) и перестановки операций суммирования и интегрирования получим
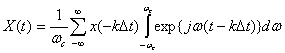 . (7)
. (7)
Вычислим интеграл
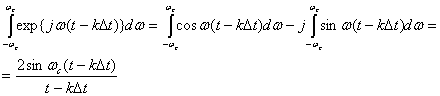 (8)
(8)
т.к. 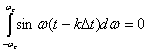 .
.
После подстановки (8) в (7) окончательно получим
![]() . (9)
. (9)
Полученное выражение представляет аналитически теорему Котельникова.
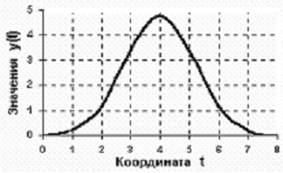
Из (9) видно, что непрерывная функция X(t) (рисунок 2, а), обладающая ограниченным спектром, может быть представлена разложением в ряд, каждый член которого выражается одинаковой функцией вида sin(x)/x (функция отсчета), но с различными коэффициентами ![]() (рисунок 2, б).
(рисунок 2, б).
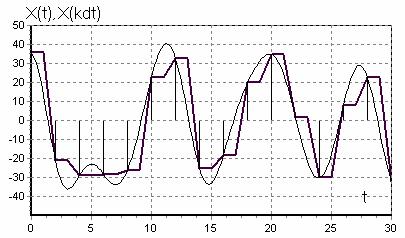
Рисунок 2, а - Функция отсчета
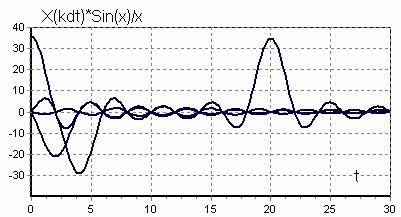
Рисунок 2, б - Функция отсчета, но с различными коэффициентами ![]()
Ряд (9) представляет собой разложение случайного процесса с координатными функциями (детерминированными функциями времени) и весовыми коэффициентами ![]() , являющимися случайными величинами, равными мгновенным значениям сигнала в точках
, являющимися случайными величинами, равными мгновенным значениям сигнала в точках ![]() .
.
Функция отсчетов в момент времени ![]() достигает максимума и равна единице. В моменты времени
достигает максимума и равна единице. В моменты времени ![]() , где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.
, где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.
Сумма (9) в каждый k-ый момент времени определяется только одним k-ым слагаемым, т.к. все остальные слагаемые в этот момент времени обращается в нуль. Внутри промежутка ![]() восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
Похожие работы
... функций в виде зависимости их значений от определенных аргументов Δвремени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой ...
... ИКМ сигнала на приемной станции; ПК пр – преобразователь кода – преобразует биполярный сигнал в однополярный; Пр СС – приемник синхросигналов – правильное декодирование и распределение сигналов по своим телефонным каналам и каналам передачи СУВ; УР – устройство разделения – разделяет кодовые группы ТЛФ каналов и СУВ; Пр СУВ – приемник групповых сигналов управления и взаимодействия – ...
... соответствует нулевому значению цветоразностного сигнала. При воспроизведении пурпурного цвета E'B-Y = 0.59, т. е.: CB=126·E'B-Y+128=202=11001010 При воспроизведении голубого цвета E'B-Y =0.3, т. е.: CB=126·E'B-Y+128=165.8=10100101 3. Графики изменения сигналов яркости и цветности во времени в строчном периоде для текстового изображения «градационный клин» Рисунок 5. Графики ...
... нельзя проводить отбор отдельных компонентов ИС по допуска, как это имело место в схемах дискретных электорадиоэлементах в ЭВМ третьего поколения. Разработка генератора на цифровых микросхемах. Для проверки и настройки цифровых интегральных микросхемах транзисторно-транзисторной логики (ТТЛ) требуются генераторы прямоугольных импульсов. Ниже описывается генератор импульсов, выполненный всего на ...

0 комментариев