Навигация
Мостиковые схемы
3.4. Мостиковые схемы
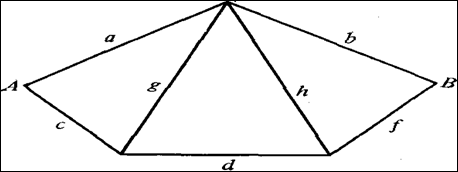
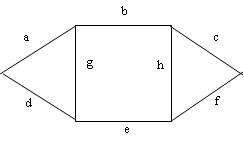
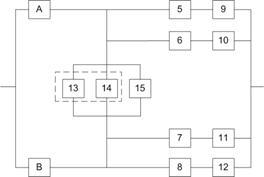
Мостиковая структура (рис. 3.2, а, б) не сводится к параллельному или последовательному типу соединения элементов, а представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (элемент 3 на рис. 3.2, а, элементы 3 и 6 на рис. 3.2, б). Работоспособность такой системы определяется не только количеством отказавших элементов, но и их положением в структурной схеме. Например, работоспособность ТС, схема которой приведена на рис. 3.2, а, будет утрачена при одновременном отказе элементов 1 и 2, или 4 и 5, или 2, 3 и 4 и т.д.. В то же время отказ элементов 1 и 5, или 2 и 4, или 1, 3 и 4, или 2, 3 и 5 к отказу системы не приводит.
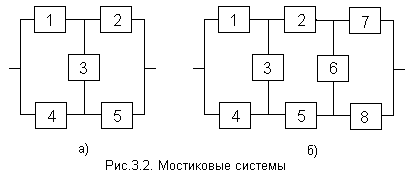
Таблица 3.3
Таблица состояний мостиковой системы
|
| Состояние | Вероятность состояния | ||||||||
| сост. | 1 | 2 | 3 | 4 | 5 | системы | в общем случае | при равнонадежных элементах | ||
| 1 | + | + | + | + | + | + | |
| ||
| 2 | + | + | + | + | - | + |
|
| ||
| 3 | + | + | + | - | + | + |
| |||
| 4 | + | + | - | + | + | + |
| |||
| 5 | + | - | + | + | + | + |
| |||
| 6 | - | + | + | + | + | + |
| |||
| 7 | + | + | + | - | - | - |
|
| ||
| 8 | + | + | - | + | - | + |
| |||
| 9 | + | - | + | + | - | + |
| |||
| 10 | - | + | + | + | - | + |
| |||
| 11 | + | + | - | - | + | + |
| |||
| 12 | + | - | + | - | + | + |
| |||
| 13 | - | + | + | - | + | + |
| |||
| 14 | + | - | - | + | + | + |
| |||
| 15 | - | + | - | + | + | + |
| |||
| 16 | - | - | + | + | + | - |
| |||
| 17 | + | + | - | - | - | - |
|
| ||
| 18 | + | - | + | - | - | - |
| |||
| 19 | - | + | + | - | - | - |
| |||
| 20 | + | - | - | - | + | - |
| |||
| 21 | - | + | - | - | + | + |
| |||
| 22 | - | - | - | + | + | - |
| |||
| 23 | + | - | - | + | - | + |
| |||
| 24 | - | + | - | + | - | - |
| |||
| 25 | - | - | + | - | + | - |
| |||
| 26 | - | - | + | + | - | - |
| |||
| 27 | + | - | - | - | - | - |
|
| ||
| 28 | - | + | - | - | - | - |
| |||
| 29 | - | - | + | - | - | - |
| |||
| 30 | - | - | - | + | - | - |
| |||
| 31 | - | - | - | - | + | - |
| |||
| 32 | - | - | - | - | - | - |
|
| ||
Для расчета надежности мостиковых систем можно воспользоваться методом прямого перебора, как это было сделано для систем “m из n“ (п. 3.3), но при анализе работоспособности каждого состояния системы необходимо учитывать не только число отказавших элементов, но и их положение в схеме (табл. 3.3). Вероятность безотказной работы системы определяется как сумма вероятностей всех работоспособных состояний:
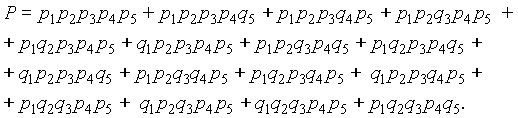 (3.21)
(3.21)
В случае равнонадёжных элементов
![]() (3.22)
(3.22)
Метод прямого перебора эффективен только при малом количестве элементов n, о чем говорилось в начале разд. 3, поскольку число состояний системы составляет ![]() . Например, для схемы на рис. 3.2,б их количество составит уже 256. Некоторое упрощение достигается, если в таблицу состояний включать только сочетания, отвечающие работоспособному (или только неработоспособному) состоянию системы в целом.
. Например, для схемы на рис. 3.2,б их количество составит уже 256. Некоторое упрощение достигается, если в таблицу состояний включать только сочетания, отвечающие работоспособному (или только неработоспособному) состоянию системы в целом.
Для анализа надежности ТС, структурные схемы которых не сводятся к параллельному или последовательному типу, можно воспользоваться также методом логических схем с применением алгебры логики (булевой алгебры). Применение этого метода сводится к составлению для ТС формулы алгебры логики, которая определяет условие работоспособности системы. При этом для каждого элемента и системы в целом рассматриваются два противоположных события - отказ и сохранение работоспособности.
Для составления логической схемы можно воспользоваться двумя методами - минимальных путей и минимальных сечений.
Рассмотрим метод минимальных путей для расчета вероятности безотказной работы на примере мостиковой схемы (рис. 3.2,а).
Минимальным путем называется последовательный набор работоспо-собных элементов системы, который обеспечивает ее работоспособность, а отказ любого из них приводит к ее отказу.
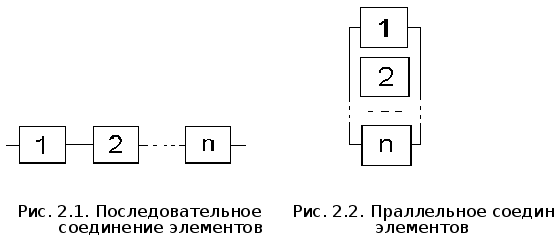
Минимальных путей в системе может быть один или несколько. Очевидно, система с последовательным соединением элементов (рис. 2.1) имеет только один минимальный путь, включающий все элементы. В системе с параллельным соединением (рис. 2.2) число минимальных путей совпадает с числом элементов и каждый путь включает один из них.
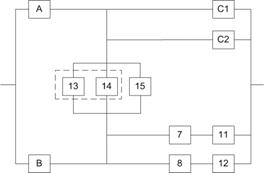
Для мостиковой системы из пяти элементов (рис. 3.2,а) минимальных путей четыре: (элементы 1 и 4), (2 и 5), (1, 3 и 5), (2, 3 и 5). Логическая схема такой системы (рис. 3.3) составляется таким образом, чтобы все элементы каждого минимального пути были соединены друг с другом последовательно, а все минимальные пути параллельно.
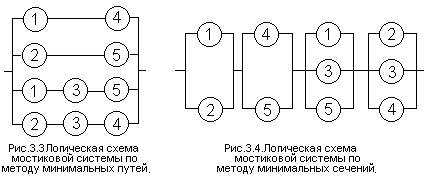
Затем для логической схемы составляется функция алгебры логики А по общим правилам расчета вероятности безотказной работы , но вместо символов вероятностей безотказной работы элементов ![]() и системы Р используются символы события (сохранения работоспособности элемента ai и системы А). Так, “отказ“ логической схемы рис. 3.3 состоит в одновременном отказе всех четырех параллельных ветвей, а “безотказная работа” каждой ветви - в одновременной безотказной работе ее элементов. Последовательное соединение элементов логической схемы соответствует логическому умножению (“И”), параллельное - логическому сложению (“ИЛИ”). Следовательно, схема рис. 3.3 соответствует утверждению: система работоспособна, если работоспособны элементы 1 и 4, или 2 и 5, или 1,3 и 5, или 2,3 и 4. Функция алгебры логики запишется:
и системы Р используются символы события (сохранения работоспособности элемента ai и системы А). Так, “отказ“ логической схемы рис. 3.3 состоит в одновременном отказе всех четырех параллельных ветвей, а “безотказная работа” каждой ветви - в одновременной безотказной работе ее элементов. Последовательное соединение элементов логической схемы соответствует логическому умножению (“И”), параллельное - логическому сложению (“ИЛИ”). Следовательно, схема рис. 3.3 соответствует утверждению: система работоспособна, если работоспособны элементы 1 и 4, или 2 и 5, или 1,3 и 5, или 2,3 и 4. Функция алгебры логики запишется:
![]() (3.23)
(3.23)
В выражении (3.23) переменные а рассматриваются как булевы, т.е. могут приниматься только два значения: 0 или 1. Тогда при возведении в любую степень k любая переменная a сохраняет свое значение: ![]() . На основе этого свойства функция алгебры логики (3.23) может быть преобразована к виду
. На основе этого свойства функция алгебры логики (3.23) может быть преобразована к виду
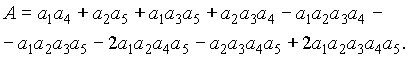 (3.24)
(3.24)
Заменив в выражении (3.24) символы событий ![]() их вероятностями
их вероятностями ![]() , получим уравнение для определения вероятности безотказной работы системы
, получим уравнение для определения вероятности безотказной работы системы
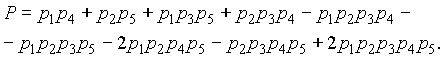 (3.25)
(3.25)
Для системы равнонадёжных элементов (![]() ) выражение (3.25) легко преобразуется в формулу (3.22).
) выражение (3.25) легко преобразуется в формулу (3.22).
Метод минимальных путей дает точное значение только для сравнительно простых систем с небольшим числом элементов. Для более сложных систем результат расчета является нижней границей вероятности безотказной работы.
Для расчета верхней границы вероятности безотказной работы системы служит метод минимальных сечений.
Минимальным сечением называется набор неработоспособных элементов, отказ которых приводит к отказу системы, а восстановление работоспособности любого из них - к восстановлению работоспособности системы. Как и минимальных путей, минимальных сечений может быть несколько. Очевидно, система с параллельным соединением элементов имеет только одно минимальное сечение, включающее все ее элементы (восстановление любого восстановит работоспособность системы). В системе с последовательным соединением элементов число минимальных путей совпадает с числом элементов, и каждое сечение включает один из них .
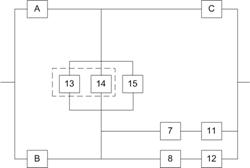
В мостиковой системе (рис. 3.2, а) минимальных сечений четыре (элементы 1 и 2), (4 и 5), (1, 3 и 5) , (2, 3 и 4). Логическая схема системы (рис.3.4) составляется таким образом, чтобы все элементы каждого мини-мального сечения были соединены друг с другом параллельно, а все мини-мальные сечения - последовательно. Аналогично методу минимальных путей, составляется функция алгебры логики. “Безотказная работа” логической системы рис. 3.4 заключается в “безотказной работе” всех последовательных участков, а “отказ” каждого из них - в одновременном “отказе” всех парал-лельно включенных элементов. Как видно, поскольку схема метода минимальных сечений формулирует условия отказа системы, в ней последо-вательное соединение соответствует логическому “ИЛИ”, а параллельное - логическому “И”. Схема рис. 3.4 соответствует формулировке: система отка-жет, если откажут элементы 1 и 2, или 4 и 5, или 1, 3 и 5, или 2, 3 и 4. Функция алгебры логики запишется
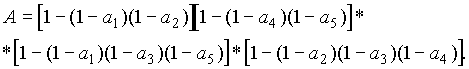 (3.26)
(3.26)
После преобразований с использованием свойств булевых переменных (3.26) приобретает форму (3.24), после замены событий их вероятностями переходит в выражение (3.25).
Таким образом, для мостиковой системы из пяти элементов верхняя и нижняя границы вероятности безотказной работы, полученные методами минимальных сечений и минимальных путей, совпали с точными значениями (3.22), полученными методом прямого перебора. Для сложных систем это может не произойти, поэтому методы минимальных путей и минимальных сечений следует применять совместно.
В ряде случаев анализа надежности ТС удается воспользоваться методом разложения относительно особого элемента, основанными на известной в математической логике теореме о разложении функции логики по любому аргументу. Согласно ей, можно записать:
![]() (3.27)
(3.27)
где ![]() и
и ![]() - вероятности безотказной работы и отказа i - го элемента,
- вероятности безотказной работы и отказа i - го элемента, ![]() и
и![]() -вероятности работоспособного состояния системы при условии, что i - й элемент абсолютно надежен и что i - й элемент отказал.
-вероятности работоспособного состояния системы при условии, что i - й элемент абсолютно надежен и что i - й элемент отказал.
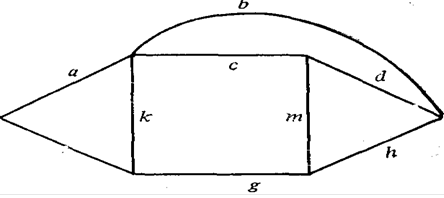
Для мостиковой схемы (рис. 3.2, а) в качестве особого элемента целесообразно выбрать диагональный элемент 3. При ![]() мостиковая схема превращается в параллельно - последовательное соединение (рис. 3.5, а), а при
мостиковая схема превращается в параллельно - последовательное соединение (рис. 3.5, а), а при ![]() - в последовательно - параллельное (рис. 3.5, б).
- в последовательно - параллельное (рис. 3.5, б).
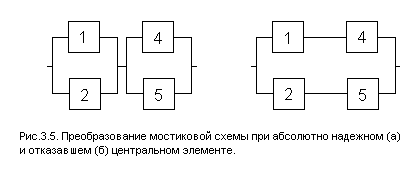
Для преобразованных схем можно записать:
![]() (3.28)
(3.28)
![]() (3.29)
(3.29)
Тогда на основании формулы (3.27) получим:
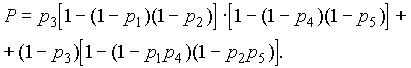 (3.30)
(3.30)
Легко убедиться, что для равнонадёжных элементов формула (3.30) об-ращается в (3.22).
Этим методом можно воспользоваться и при разложении относительно нескольких “особых” элементов. Например, для двух элементов (i, j) выражение (3.27) примет вид:
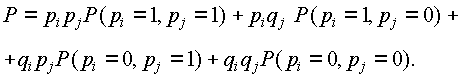 (3.31)
(3.31)
Вероятность безотказной работы мостиковой схемы (рис. 3.2, б) при разложении относительно диагональных элементов 3 и 6 по (3.31) определится:
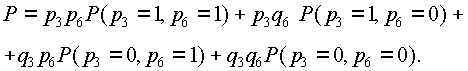 (3.32)
(3.32)
Вероятности ![]() легко ставить, выполнив предварительно преобразованные схемы, подобно рис. 3.5, а, б.
легко ставить, выполнив предварительно преобразованные схемы, подобно рис. 3.5, а, б.
Похожие работы
... доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д.. 3. РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ Расчеты показателей безотказности ТС обычно проводятся в предпо-ложении, что как вся система, так и любой ее элемент могут находиться только в одном ...
... G1=M (-1) Учитывая проверку на связность полученного суперграфа, размерность которого равна n, получим оценку сложности метода “разбиения" Qn=M (-1) +M (-1). 3.2 Разработка алгоритма оценки структурной надежности радиотехнических систем методом статистического моделирования Сеть связи задают в виде вероятностной матрицы смежности P=||pij||s,s, где Pij=kg (i,j) (i,j=1…S; i¹ ...
... P-вероятность безотказной работы исходной системы P` - вероятность безотказной работы системы с повышенной надежностью P`` - вероятность безотказной работы системы со структурным резервированием По графику находим время, где вероятность безотказной работы исходной системы равна 90%, это 79738,04 ч. 11. Расчет показывает (таблица 1), что наименьшее значение вероятности безотказной работы имеют ...
... частот информационного цифрового сигнала. В этом случае применение на приеме метода ШОУ и обратное преобразование ШПС позволяют получить требуемую достоверность информации. 2. Способы повышения достоверности передачи и приема сообщений При передаче телемеханических сигналов под воздействием мешающих факторов (помехи, неисправности, изменение параметров и т.п.) происходят определенные изменения ...

0 комментариев