Навигация
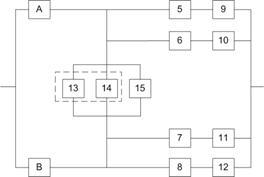
Преобразованная схема изображена на рис. 7.2
7. Преобразованная схема изображена на рис. 7.2.
8. Элементы A, B, C, D и Е образуют (рис. 7.2) мостиковую систему, которую можно заменить квазиэлементом G. Для расчета вероятности безотказной работы воспользуемся методом разложения относительно особого элемента (см. раздел 3.4), в качестве которого выберем элемент С. Тогда
![]() (7.7)
(7.7)
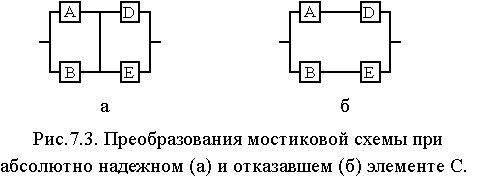
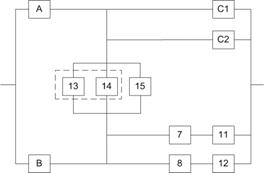
где ![]() - вероятность безотказной работы мостиковой схемы при абсолютно надежном элементе С (рис. 7.3, а),
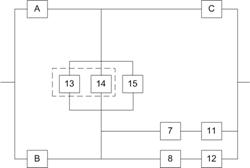
- вероятность безотказной работы мостиковой схемы при абсолютно надежном элементе С (рис. 7.3, а), ![]() - вероятность безотказной работы мостиковой схемы при отказавшем элементе С (рис. 7.3, б).
- вероятность безотказной работы мостиковой схемы при отказавшем элементе С (рис. 7.3, б).
Учитывая, что ![]() , получим
, получим
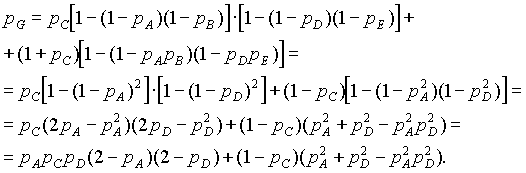 (7.8)
(7.8)
9. После преобразований схема изображена на рис. 7.4.
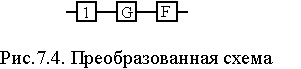
10. В преобразованной схеме (рис. 7.4) элементы 1, G и F образуют последовательное соединение. Тогда вероятность безотказной работы всей системы
![]() (7.9)
(7.9)
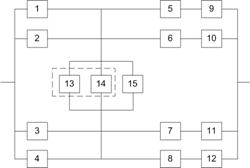
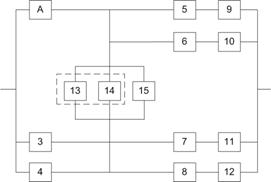
11. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 (рис. 7.1) подчиняются экспоненциальному закону:
![]() (7.10)
(7.10)
12. Результаты расчетов вероятностей безотказной работы элементов 1 - 15 исходной схемы по формуле (7.10) для наработки до ![]() часов представлены в таблице 7.1.
часов представлены в таблице 7.1.
13. Результаты расчетов вероятностей безотказной работы квазиэле-ментов A, B, C, D, E, F и G по формулам (7.1) - (7.6) и (7.8) также представлены в таблице 7.1.
14. На рис. 7.5 представлен график зависимости вероятности безотказной работы системы P от времени (наработки) t.
15. По графику (рис. 7.5, кривая P) находим для ![]()
![]()
![]() - процентную наработку системы
- процентную наработку системы ![]() ч.
ч.
16. Проверочный расчет при ![]() ч показывает (таблица 7.1), что
ч показывает (таблица 7.1), что ![]() .
.
17. По условиям задания повышенная ![]() - процентная наработка сис-темы
- процентная наработка сис-темы ![]() ч.
ч.
Таблица 7.1
Расчет вероятности безотказной работы системы
| Элемент | l i, | Наработка t, x 106 ч | ||||||||||||||
| x10-6 ч-1 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 1,9 | 2,85 | ||||||||
| 1 | 0,001 | 0,9995 | 0,9990 | 0,9985 | 0,9980 | 0,9975 | 0,9970 | 0,9981 | 0,9972 | |||||||
| 2 - 5 | 0,1 | 0,9512 | 0,9048 | 0,8607 | 0,8187 | 0,7788 | 0,7408 | 0,8270 | 0,7520 | |||||||
| 6,7 | 0,01 | 0,9950 | 0,9900 | 0,9851 | 0,9802 | 0,9753 | 0,9704 | 0,9812 | 0,9719 | |||||||
| 8 - 11 | 0,2 | 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,6839 | 0,5655 | |||||||
| 12 - 15 | 0,5 | 0,7788 | 0,6065 | 0,4724 | 0,3679 | 0,2865 | 0,2231 | 0,3867 | 0,2405 | |||||||
| A, B | - | 0,9976 | 0,9909 | 0,9806 | 0,9671 | 0,9511 | 0,9328 | 0,9701 | 0,9385 | |||||||
| C | - | 0,9900 | 0,9801 | 0,9704 | 0,9608 | 0,9512 | 0,9417 | 0,9628 | 0,9446 | |||||||
| D, E | - | 0,9909 | 0,9671 | 0,9328 | 0,8913 | 0,8452 | 0,7964 | 0,9001 | 0,8112 | |||||||
| F | - | 0,9639 | 0,8282 | 0,6450 | 0,4687 | 0,3245 | 0,2172 | 0,5017 | 0,2458 | |||||||
| G | - | 0,9924 | 0,9888 | 0,9863 | 0,9820 | 0,9732 | 0,9583 | 0,9832 | 0,9594 | |||||||
| P | - | 0,9561 | 0,8181 | 0,6352 | 0,4593 | 0,3150 | 0,2075 | 0,4923 | 0,2352 | |||||||
| 12` - 15` | 0,322 | 0,8513 | 0,7143 | 0,6169 | 0,5252 | 0,4471 | 0,3806 | 0,5424 | 0,3994 | |||||||
| F` | - | 0,9883 | 0,9270 | 0,8397 | 0,7243 | 0,6043 | 0,4910 | 0,7483 | 0,5238 | |||||||
| P` | - | 0,9803 | 0,9157 | 0,8270 | 0,7098 | 0,5866 | 0,4691 | 0,7343 | 0,5011 | |||||||
| 16 - 18 | 0,5 | 0,7788 | 0,6065 | 0,4724 | 0,3679 | 0,2865 | 0,2231 | 0,3867 | 0,2405 | |||||||
| F`` | - | 0,9993 | 0,9828 | 0,9173 | 0,7954 | 0,6413 | 0,4858 | 0,8233 | 0,5311 | |||||||
| P`` | - | 0,9912 | 0,9708 | 0,9034 | 0,7795 | 0,6226 | 0,4641 | 0,8079 | 0,5081 | |||||||
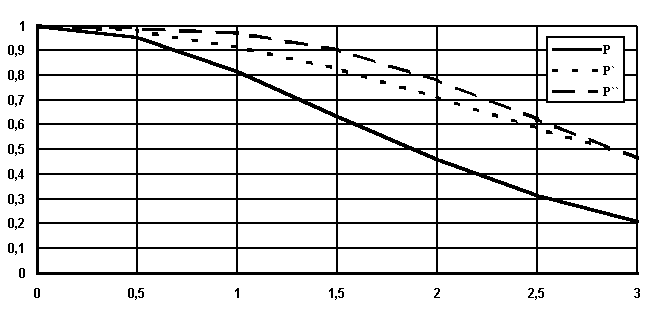
Рис 7.5. Изменение вероятности безотказной работы исходной системы (Р), системы с повышенной надежностью (Р`) и системы со структурным резервированием элементов (Р``).
18. Расчет показывает (таблица 7.1), что при ![]() ч для элементов преобразованной схемы (рис. 7.4)
ч для элементов преобразованной схемы (рис. 7.4) ![]() ,
, ![]() и
и ![]() . Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (система “2 из 4” в исходной схеме (рис. 7.1)) и именно увеличение его надежности даст максимальное увеличение надежности системы в целом .
. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент F (система “2 из 4” в исходной схеме (рис. 7.1)) и именно увеличение его надежности даст максимальное увеличение надежности системы в целом .
19. Для того, чтобы при ![]() ч система в целом имела вероятность безотказной работы
ч система в целом имела вероятность безотказной работы ![]() , необходимо, чтобы элемент F имел вероятность безотказной работы (см. формулу (7.9))
, необходимо, чтобы элемент F имел вероятность безотказной работы (см. формулу (7.9))
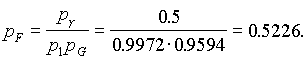 (7.11)
(7.11)
При этом значении элемент F останется самым ненадежным в схеме (рис. 7.4) и рассуждения в п.18 останутся верными.
Очевидно, значение ![]() , полученное по формуле (7.11), является мини-мальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях
, полученное по формуле (7.11), является мини-мальным для выполнения условия увеличения наработки не менее, чем в 1.5 раза, при более высоких значениях ![]() увеличение надежности системы будет большим.
увеличение надежности системы будет большим.
20. Для определения минимально необходимой вероятности безотказной работы элементов 12 - 15 (рис. 7.1) необходимо решить уравнение (7.6) относительно ![]() при
при ![]() . Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями , более целесообразно использовать графо-аналитический метод. Для этого по данным табл. 7.1 строим график зависимости
. Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями , более целесообразно использовать графо-аналитический метод. Для этого по данным табл. 7.1 строим график зависимости ![]() . График представлен на рис. 7.6.
. График представлен на рис. 7.6.
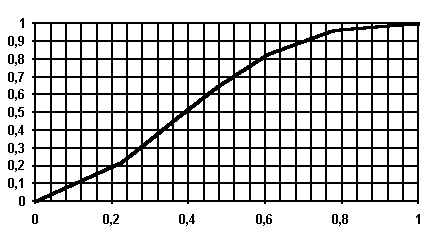
Рис. 7.6. Зависимость вероятности безотказной работы системы “2 из 4” от вероятности безотказной работы ее элементов.
21. По графику при ![]() находим
находим ![]() .
.
22. Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (7.10), то для элементов 12 - 15 при ![]() находим
находим
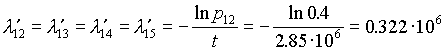 ч
ч![]() . (7.12)
. (7.12)
23. Таким образом, для увеличения ![]() - процентной наработки ситемы необходимо увеличить надежность элементов 12, 13, 14 и 15 и снизить интенсивность их отказов с
- процентной наработки ситемы необходимо увеличить надежность элементов 12, 13, 14 и 15 и снизить интенсивность их отказов с ![]() до
до ![]() ч
ч![]() , т.е. в 1.55 раза.
, т.е. в 1.55 раза.
24. Результаты расчетов для системы с увеличенной надежностью элементов 12, 13, 14 и 15 приведены в таблице 7.1. Там же приведены расчетные значения вероятности безотказной работы системы “2 из 4” F` и системы в целом P`. При ![]() ч вероятность безотказной работы системы
ч вероятность безотказной работы системы ![]() , что соответствует условиям задания. График приведен на рис 7.5.
, что соответствует условиям задания. График приведен на рис 7.5.
25. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования - по тем же соображениям (см. п. 18) также выбираем элемент F, вероятность безотказной работы которого после резервирования должна быть не ниже ![]() (см. формулу ( 7.11 )).
(см. формулу ( 7.11 )).
26. Для элемента F - системы “2 из 4” - резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция ![]() дискретна.
дискретна.
27. Для повышения надежности системы “2 из 4” добавляем к ней элементы, идентичные по надежности исходным элементам 12 - 15, до тех пор, пока вероятность безотказной работы квазиэлемента F не достигнет заданного значения.
Для расчета воспользуемся комбинаторным методом (см. раздел 3.3) :
- добавляем элемент 16, получаем систему “2 из 5”:
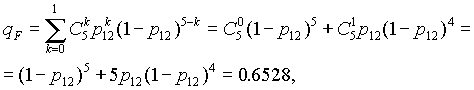 (7.13)
(7.13)
![]() (7.14)
(7.14)
- добавляем элемент 17, получаем систему “2 из 6”:
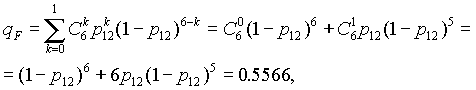 (7.15)
(7.15)
![]() (7.16)
(7.16)
- добавляем элемент 18, получаем систему “2 из 7”:
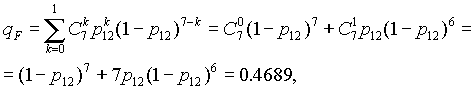 (7.17)
(7.17)
![]() (7.18)
(7.18)
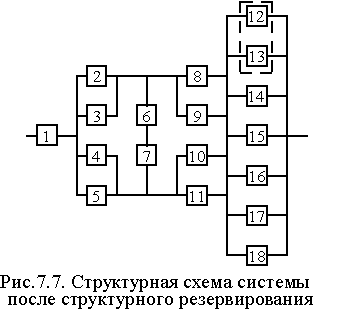
28. Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рис. 7.1) систему “2 из 4” достроить элементами 16, 17 и 18 до системы “2 из 7” (рис. 7.7).
29. Результаты расчетов вероятностей безотказной работы системы “2 из 7” F`` и системы в целом P`` представлены в таблице 7.1.
30. Расчеты показывают, что при ![]() ч
ч ![]() , что соот-ветствует условию задания.
, что соот-ветствует условию задания.
31. На рис. 7.5 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов 12 - 15 (кривая ![]() ) и после структурного резервирования (кривая
) и после структурного резервирования (кривая ![]() ).
).
Выводы:
1. На рис. 7.5 представлена зависимость вероятности безотказной работы системы (кривая ![]() ). Из графика видно, что 50% - наработка исходной системы составляет
). Из графика видно, что 50% - наработка исходной системы составляет ![]() часов.
часов.
2. Для повышения надежности и увеличения 50% - наработки системы в 1.5 раза (до ![]() часов) предложены два способа:
часов) предложены два способа:
а) повышение надежности элементов 12, 13, 14 и 15 и уменьшение их отказов с ![]() до
до ![]() ч
ч![]() ;
;
б) нагруженное резервирование основных элементов 12, 13, 14 и 15 идентичными по надежности резервными элементами 16, 17 и 18 (рис. 7.7).
3. Анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис. 7.5) показывает, что второй способ повышения надежности системы (структурное резервирование) предпочтительнее первого, так как в период наработки до ![]() часов вероятность безотказной работы системы при структурном резервировании (кривая
часов вероятность безотказной работы системы при структурном резервировании (кривая ![]() ) выше, чем при увеличе-нии надежности элементов (кривая
) выше, чем при увеличе-нии надежности элементов (кривая ![]() ).
).
Таблица 6.1
Численные значения параметров к заданию
| № | g, | Интенсивности отказов элементов, l i , x10-6 1/ч | ||||||||||||||||||||||
| вар. | % | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||||||
| 1 | 90 | 0.1 | 1.0 | 0.5 | 1.0 | 0.1 | ||||||||||||||||||
| 2 | 95 | 0.2 | 0.5 | 1.0 | 0.1 | |||||||||||||||||||
| 3 | 80 | 0.1 | 1.0 | 2.0 | 1.0 | 5.0 | 0.2 | |||||||||||||||||
| 4 | 70 | 0.05 | 1.0 | 0.5 | 0.2 | 0.02 | ||||||||||||||||||
| 5 | 50 | 0.01 | 0.05 | 0.1 | 0.5 | 1.0 | ||||||||||||||||||
| 6 | 75 | 0.01 | 0.05 | 1.0 | 0.05 | 0.1 | - | |||||||||||||||||
| 7 | 65 | 0.05 | 0.5 | 0.05 | 0.005 | 0.1 | 0.2 | 0.1 | - | |||||||||||||||
| 8 | 85 | 0.1 | 0.5 | 0.2 | 0.01 | 0.5 | 0.1 | - | ||||||||||||||||
| 9 | 60 | 0.03 | 0.5 | 0.2 | 1.0 | 0.03 | 0.1 | - | ||||||||||||||||
| 10 | 50 | 0.1 | 0.5 | 1.0 | 0.5 | 1.0 | 0.1 | - | ||||||||||||||||
| 11 | 75 | 0.05 | 0.2 | 0.5 | 0.2 | 0.1 | ||||||||||||||||||
| 12 | 65 | 0.02 | 0.1 | 1.0 | 2.0 | 0.1 | 0.05 | |||||||||||||||||
| 13 | 70 | 0.01 | 0.2 | 0.1 | 1.0 | 0.5 | 0.1 | - | ||||||||||||||||
| 14 | 50 | 0.01 | 0.1 | 10.0 | 0.2 | 10.0 | 0.5 | - | ||||||||||||||||
| 15 | 85 | 0.01 | 1.0 | 5.0 | 0.2 | 5.0 | 0.1 | - | ||||||||||||||||
| 16 | 80 | 0.1 | 1.0 | 2.0 | 1.0 | 5.0 | 3.0 | 1.0 | 0.05 | |||||||||||||||
| 17 | 95 | 0.1 | 5.0 | 1.0 | 5.0 | 10.0 | 5.0 | 1.0 | 0.2 | |||||||||||||||
| 18 | 60 | 0.01 | 1.0 | 0.1 | - | |||||||||||||||||||
| 19 | 75 | 0.1 | 5.0 | 0.5 | 5.0 | 1.0 | 3.0 | 1.0 | 5.0 | 0.5 | 5.0 | |||||||||||||
| 20 | 90 | 0.1 | 10.0 | 20.0 | 10.0 | |||||||||||||||||||
| 21 | 90 | 0.1 | 1.0 | 0.5 | 2.0 | 0.5 | 0.2 | 1.0 | ||||||||||||||||
| 22 | 80 | 1.0 | 0.2 | 0.5 | 1.0 | 0.5 | 1.0 | 1.0 | 0.1 | |||||||||||||||
| 23 | 70 | 0.5 | 0.2 | 1.0 | 0.5 | 1.0 | 0.5 | 1.0 | 0.2 | 0.5 | 1.0 | 0.2 | ||||||||||||
| 24 | 60 | 1.0 | 2.0 | 4.0 | 2.0 | 4.0 | 5.0 | 1.0 | ||||||||||||||||
| 25 | 50 | 0.5 | 10.0 | 0.5 | 5.0 | 0.8 | 5.0 | 1.0 | 5.0 | |||||||||||||||
| 26 | 60 | 1.0 | 2.0 | 3.0 | 5.0 | 2.0 | 5.0 | 1.0 | ||||||||||||||||
| 27 | 70 | 5.0 | 10.0 | 15.0 | 10.0 | 10.0 | 15.0 | 10.0 | ||||||||||||||||
| 28 | 80 | 1.0 | 2.0 | 5.0 | 2.0 | 1.0 | ||||||||||||||||||
| 29 | 90 | 5.0 | 20.0 | 50.0 | 30.0 | 1.0 | ||||||||||||||||||
| 30 | 80 | 2.0 | 1.0 | 2.0 | 1.0 | 5.0 | 2.0 | 5.0 | 2.0 | 1.0 | 2.0 | 1.0 | 2.0 | 1.0 | ||||||||||
| 31 | 70 | 2.0 | 1.0 | 2.0 | 1.0 | 5.0 | 2.0 | 5.0 | 2.0 | 1.0 | 2.0 | 1.0 | 2.0 | 1.0 | ||||||||||
| 32 | 60 | 5.0 | 2.0 | 5.0 | 1.0 | 2.0 | 3.0 | 1.0 | ||||||||||||||||
| 33 | 60 | 1.0 | 2.0 | 3.0 | 4.0 | 2.0 | 3.0 | 5.5 | 0.2 | 0.5 | ||||||||||||||
| 34 | 90 | 6.0 | 3.0 | 6.0 | 3.0 | 6.0 | 20.0 | 10.0 | ||||||||||||||||
| 35 | 95 | 1.0 | 2.0 | 1.0 | 2.0 | 1.0 | 5.0 | |||||||||||||||||
| 36 | 80 | 2.0 | 1.0 | 0.6 | ||||||||||||||||||||
| 37 | 70 | 10.0 | 30.0 | 5.0 | 2.0 | |||||||||||||||||||
| 38 | 90 | 3.0 | 2.0 | 1.0 | 2.0 | 3.0 | 2.0 | |||||||||||||||||
| 39 | 90 | 8.0 | 3.0 | 5.0 | 2.0 | |||||||||||||||||||
| 40 | 80 | 2.0 | 5.0 | 8.0 | 2.0 | 5.0 | 8.0 | |||||||||||||||||
| № | g, | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||||||
| вар. | % | Интенсивности отказов элементов, l i , x10-6 1/ч | ||||||||||||||||||||||
ПРИЛОЖЕНИЕ
Биномиальные коэффициенты 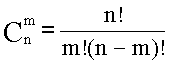
| n | m | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 1 | ||||||||||
| 1 | 1 | 1 | |||||||||
| 2 | 1 | 2 | 1 | ||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |
| 10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
| 11 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 |
| 12 | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 |
| 13 | 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 |
| 14 | 1 | 14 | 91 | 364 | 1001 | 2002 | 3003 | 3432 | 3003 | 2002 | 1001 |
| 15 | 1 | 15 | 105 | 455 | 1365 | 3003 | 5005 | 6435 | 6435 | 5005 | 3003 |
| 16 | 1 | 16 | 120 | 560 | 1820 | 4368 | 8008 | 11440 | 12870 | 11440 | 8008 |
| 17 | 1 | 17 | 136 | 680 | 2380 | 6188 | 12376 | 19448 | 24310 | 24310 | 19448 |
| 18 | 1 | 18 | 153 | 816 | 3060 | 8568 | 18564 | 31824 | 43758 | 48620 | 43758 |
| 19 | 1 | 19 | 171 | 969 | 3876 | 11628 | 27132 | 50388 | 75582 | 92378 | 92378 |
| 20 | 1 | 20 | 190 | 1140 | 4845 | 15504 | 38760 | 77520 | 125970 | 167960 | 184756 |
Примечание: Для m>10 можно воспользоваться свойством симметрии:
![]()
Похожие работы
... доработки элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д.. 3. РАСЧЕТЫ СТРУКТУРНОЙ НАДЕЖНОСТИ СИСТЕМ Расчеты показателей безотказности ТС обычно проводятся в предпо-ложении, что как вся система, так и любой ее элемент могут находиться только в одном ...
... G1=M (-1) Учитывая проверку на связность полученного суперграфа, размерность которого равна n, получим оценку сложности метода “разбиения" Qn=M (-1) +M (-1). 3.2 Разработка алгоритма оценки структурной надежности радиотехнических систем методом статистического моделирования Сеть связи задают в виде вероятностной матрицы смежности P=||pij||s,s, где Pij=kg (i,j) (i,j=1…S; i¹ ...
... P-вероятность безотказной работы исходной системы P` - вероятность безотказной работы системы с повышенной надежностью P`` - вероятность безотказной работы системы со структурным резервированием По графику находим время, где вероятность безотказной работы исходной системы равна 90%, это 79738,04 ч. 11. Расчет показывает (таблица 1), что наименьшее значение вероятности безотказной работы имеют ...
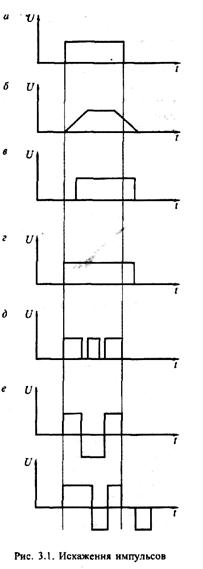
... частот информационного цифрового сигнала. В этом случае применение на приеме метода ШОУ и обратное преобразование ШПС позволяют получить требуемую достоверность информации. 2. Способы повышения достоверности передачи и приема сообщений При передаче телемеханических сигналов под воздействием мешающих факторов (помехи, неисправности, изменение параметров и т.п.) происходят определенные изменения ...

0 комментариев