Введение в неопределённые уравнения
Когда мы обдумываем решение той или иной задачи, необходимо обращать внимание на то, какие в ней используются величины. Целые или дробные? Положительные или отрицательные? Ведь незначительная деталь помогает не только устранить ошибку в решении той или иной задачи, но и найти само решение. Разберем это на примере.
Пусть у Миши (заранее извиняюсь, если посетитель сайта Михаил) есть пятирублёвые и ,допустим, восьмирублевые монеты. Всего их на сумму тридцать девять рублей. Сколько монет по пять рублей и сколько по восемь у Миши.
Кажется, что тут не хватает данных, если, например, через x обозначить кол-во 5-рублёвых монет, а за y - 8-рублёвых монет, то условие самой задачи позволяет написать одно единственное уравнение:
![]()
Эти и другие уравнения и их системы, в которых число неизвестных превышает число уравнений, называют неопределёнными.
Из условия видно, что кол-во монет не может измеряться нецелыми или отрицательными числами. Значит, если x - целое неотрицательное число, то и:
![]()
должно быть неотрицательным и целым. А значит, нужно, чтобы выражение 39 - 5x без остатка делилось на 8. С помощью подбора можно убедится, что это возможно при x = 3. Отсюда, y = 3.
Перебор вариантов не удобен, когда мы работаем с большими числами. Гораздо лучше воспользоваться методом рассевания или методом спуска, который придумали древнеиндийские математики. О методе спуска будет сказано чуть ниже.
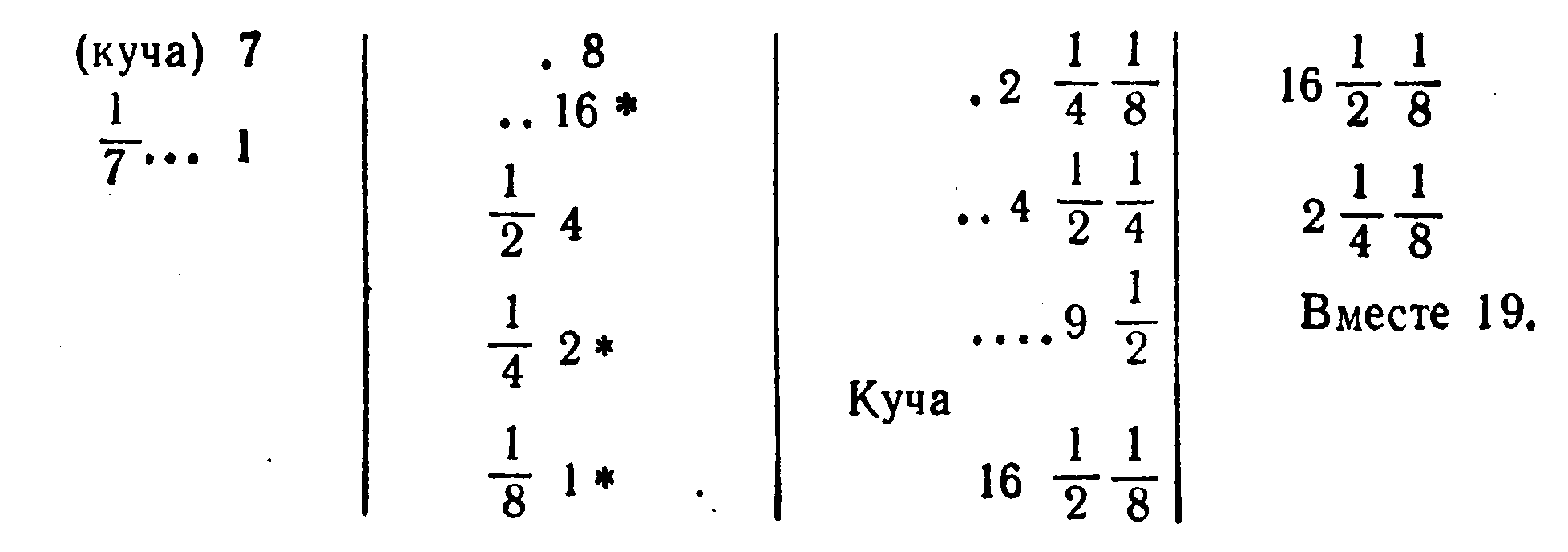
Метод спуска ![]()
![]() (материал взят из энциклопедии Аванта+ "Математика")
(материал взят из энциклопедии Аванта+ "Математика")
Продолжим рассмотрение неопределённого уравнения вида:
![]()
где a, b, c - известные целые коэффициенты.
Разберём это всё на знакомом примере:
![]()
Выберем неизвестное, имеющее наименьший коэффициент, и выразим его через другое неизвестное:
![]()
Теперь выделим целую часть:
![]()
Всё число будет целым, если целым окажется значение (4 — 3у)/5. Это возможно лишь тогда когда число (4 — 3у) без остатка делится на 5. Вводя дополнительную целочисленную переменную z, последнее условие запишем в виде
![]()
Мы пришли к уравнению такого же типа, как и исходное, но уже с меньшими коэффициентами. Решать его теперь нужно относительно переменных y и z.
Продолжаем действовать всё по тому же принципу:
![]()
Для того чтобы у оказалось целым, необходимо, чтобы число 1 - 2z без остатка делилось на 3: 1 - 2z = 3u (вновь введена дополнительная переменная u, принимающая только целые значения). Отсюда по уже отработанной схеме получаем:
![]()
Продолжим... Число z будет целым, если число 1 - u без остатка делится на 2: 1 - u = 2v, где v — произвольное целое. Отсюда u =1 - 2v. Дробей больше нет, спуск закончен.
Осталось теперь благополучно «подняться вверх». Выразим через переменную v сначала z, потом у и, наконец, х:
![]()
![]()
![]()
Формулы х = 3 + 8v, y = 3 - 5v представляют общее решение исходного уравнения в целых числах. А если нас интересуют только неотрицательные целые числа, то среди всех целых решений нужно выбрать такие, для которых
![]()
![]()
и, стало быть,
![]()
Совместно эти неравенства могут выполняться лишь при v = 0. В этом случае x = 3, y = 3. То есть у Миши было 3 5-рублёвые монеты и 3 8-рублёвые монеты.
Вообще, целые решения у уравнения вида
![]()
могут быть не всегда. Более того, если на НОД (наибольший общий делитель) a и b делится c, тогда и только тогда, уравнение разрешимо в целых чис
Похожие работы
... в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. . Как составлял и решал Диофант квадратные уравнения , В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится ...
... . Общая теория решения Диофантовых уравнений 1-й степени была создана в 17 веке. К началу 19 века трудами П. Ферма , Дж. Виллса, Л. Эйлера, Ж. Лагранжа и К. Гауса в основном было исследовано Диофантово уравнение вида ax²+bxy+cy²+dx+ey+f=0, где а,b,c,d,e,f- целые числа, то есть общее неоднородное уравнение 2-й степени с двумя неизвестными. Перейдем теперь к одной из самых ...
... . В XVIII в. из математического анализа выделился ряд важных математических дисциплин: теория дифференциальных уравнений, вариационное исчисление. В это время началась разработка теории вероятностей. 3. Развитие математики в России в XVIII-XIX столетиях Математическое образование в России находилось в 9—13 веках на уровне наиболее культурных стран Восточной и Западной Европы. Затем оно ...
... научного знания, с принципами построения научных теорий в единстве и противоположности математики и естественных и гуманитарных наук, с критериями истинности в разных формах человеческой деятельности. Заключение В исследовании внимание уделяется поиску конкретных новых событий и явлений и последовательному изложению выверенных фактов истории развития методики преподавания математики в России
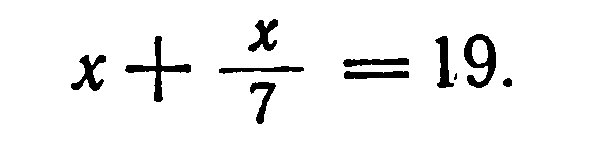
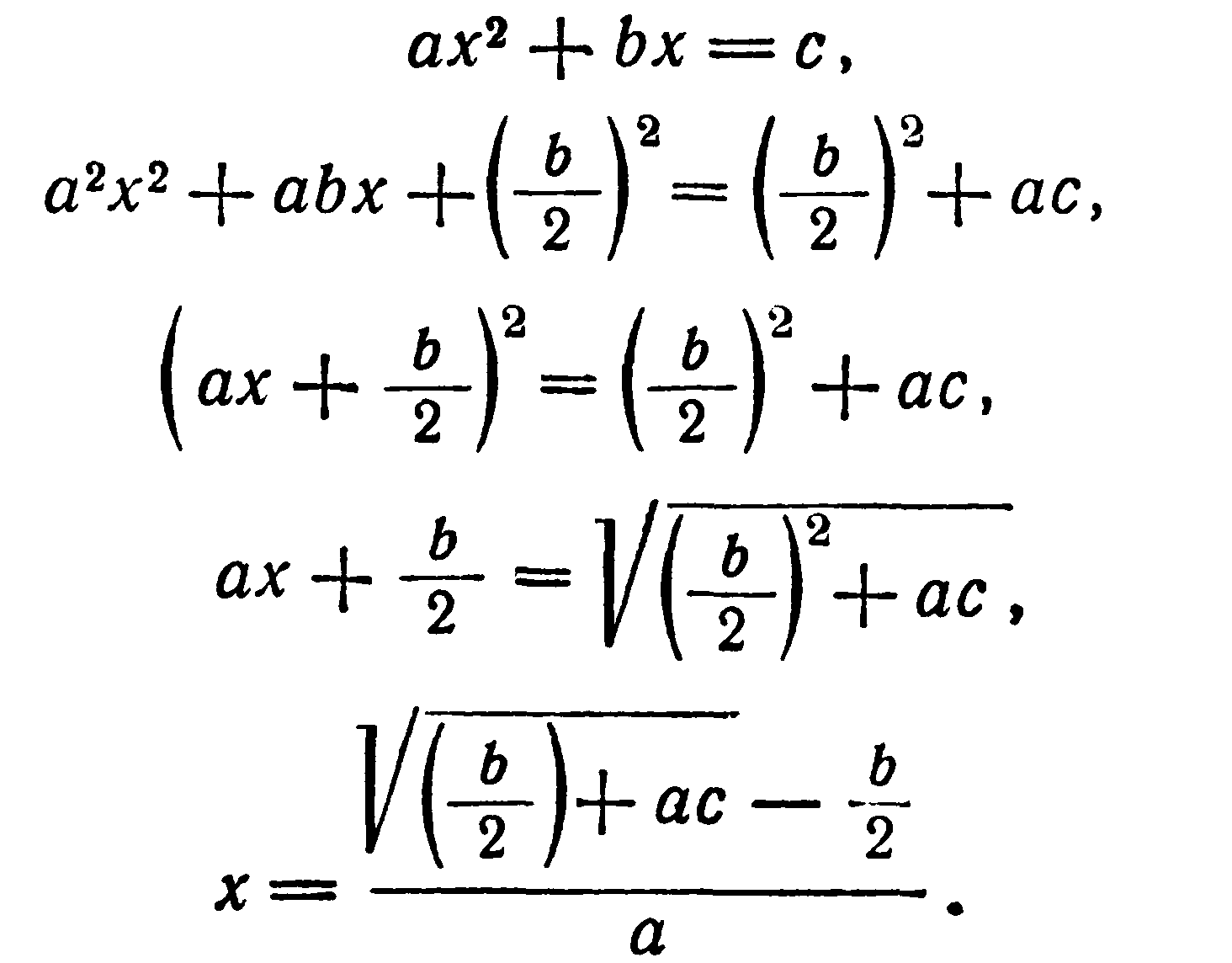

0 комментариев