y=a уравнение регрессии.
Таблица 1
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 1.35 | 1.09 | 6.46 | 3.15 | 5.80 | 7.20 | 8.07 | 8.12 | 8.97 | 10.66 |
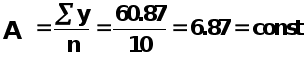
Оценка значимости коэффициентов регрессии.
Выдвигается и проверяется гипотеза о том что истинное значение коэффициента регрессии=0.
Для проверки гипотезы используется критерий Стьюдента.
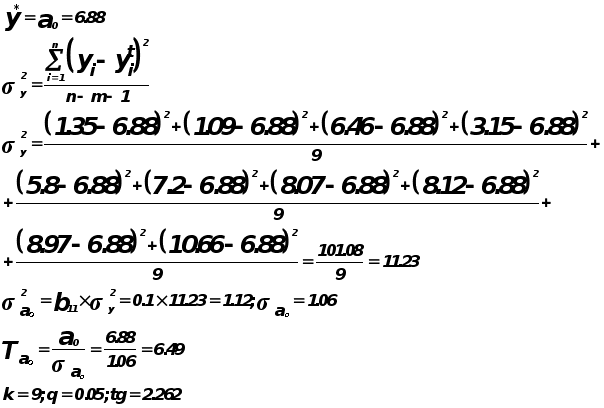
к-т является
значимым и
нулевую гипотезу
отвергаем.
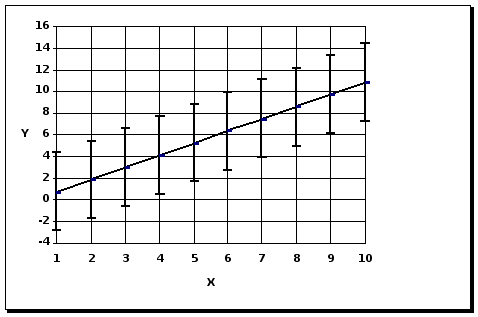
График 1
-
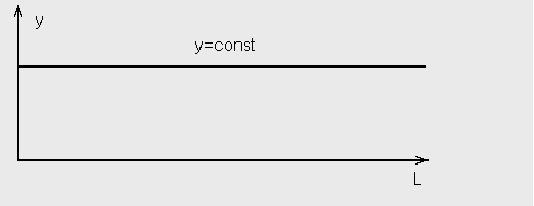
уравнение
регрессии
Таблица 2
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 1.35 | 1.09 | 6.46 | 3.15 | 5.80 | 7.20 | 8.07 | 8.12 | 8.97 | 10.66 |
Запишем матрицу X
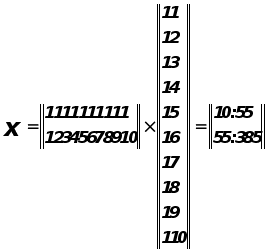
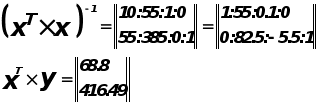
Система нормальных уравнений.
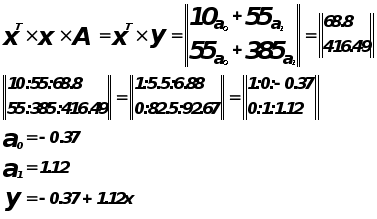
Оценка значимости коэффициентов регрессии.
Для проверки нулевой гипотезы используется критерий Стьюдента..
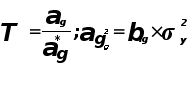
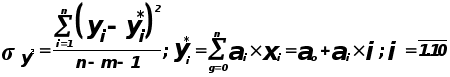
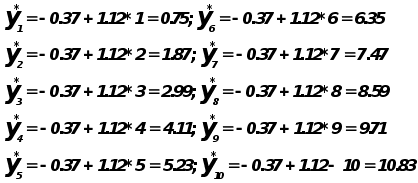
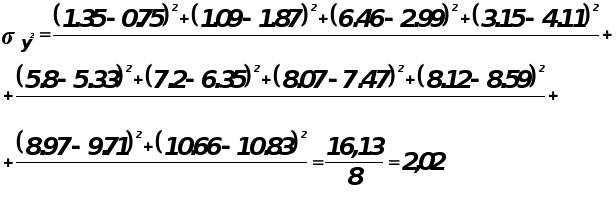
Коэффициент ai является значимости, т.к. не попал в интервал.
Проверка адекватности модели по критерию Фишера.
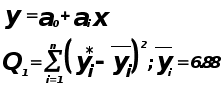
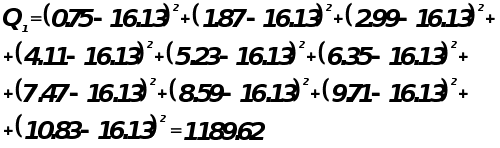
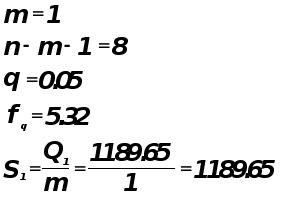
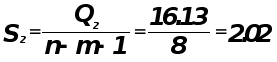
Критерий Фишера.
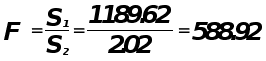
отсюда линия
регрессии
адекватна
отраксает
исходную информацию,
гипотеза о
равенстве мат.
Ожиданий отвергается.
Проверка адекватности модели по коэффициенту детерминации или множественная корреляция.
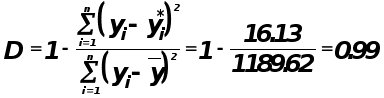
регрессионная
модель адекватна
Коэффициент множественной корреляции:
Таблица 3
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 1.35 | 1.09 | 6.46 | 3.15 | 5.80 | 7.2 | 8.07 | 8.12 | 8.97 | 10.66 |
Приведем квадратное уравнение к линейной форме:
;
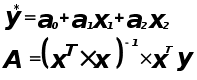
Запишем матрицу X.
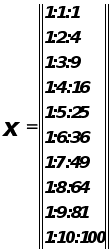
Составим матрицу Фишера.
Система
нормальных
уравнений.
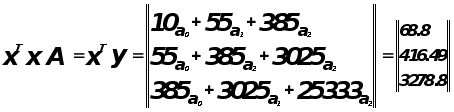
Решим ее методом Гаусса.
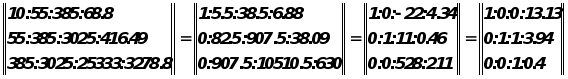
Уравнение регрессии имеет вид:
Оценка значимости коэффициентов регрессии.
Для проверки нулевой гипотезы используем критерий Стьюдента.
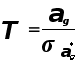
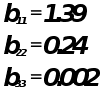
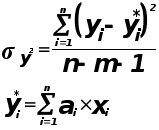
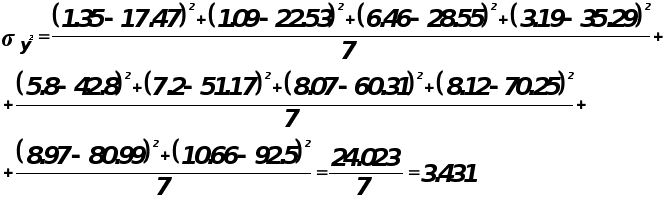
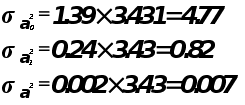
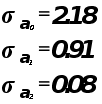
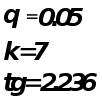
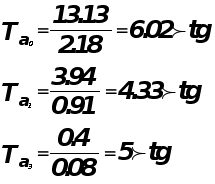
Коэффициенты
значимые
коэффициенты.
Проверка адекватности модели по критерию Фишера.
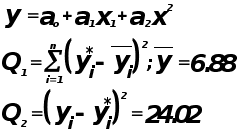
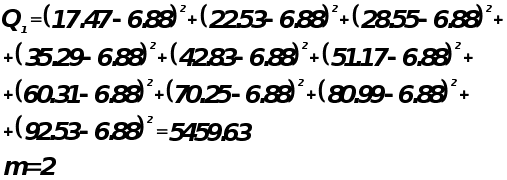
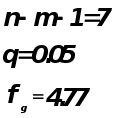
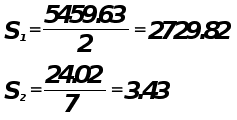
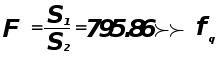гипотеза
о равенстве
математического
ожидания отвергается.
Проверка адекватности модели по коэффициенту детерминации или множественной корреляции.
Коэффициент детерминации :
-
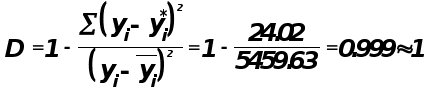
регрессионная
модель адекватна.
Коэффициент
множественной
корреляции
Таблица 4
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 0,75 | 1,87 | 2,99 | 4,11 | 5,23 | 6,35 | 7,47 | 8,59 | 9,71 | 10,83 |
График 2
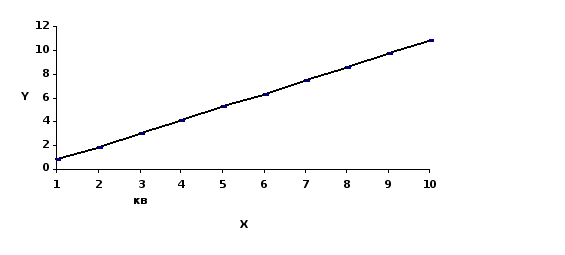
Таблица 5
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
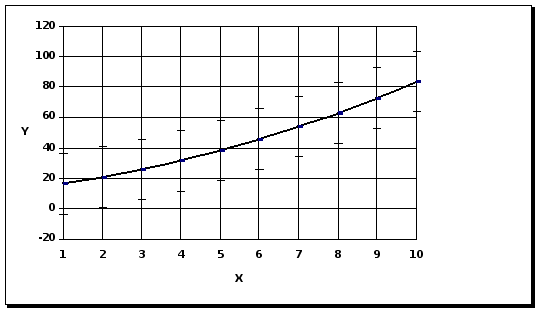
| y | 16.57 | 20.81 | 25.85 | 31.69 | 38.3 | 45.8 | 54 | 63.05 | 72.9 | 83.53 |
График 3
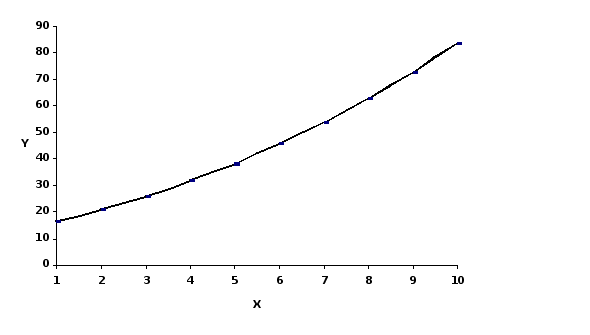
Использование регрессионной модели
для
прогнозирования
изменения
показателя
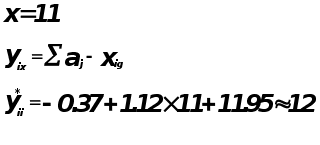
Оценка точности прогноза.
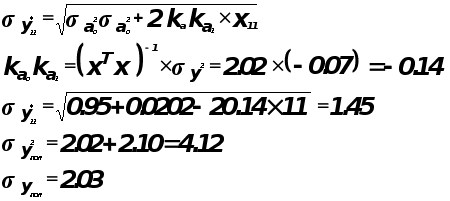
Построим доверительный интервал для заданного уровня надежности.
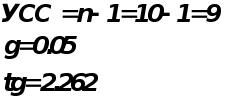
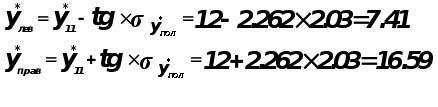
С вероятностью
0,05 этот интервал
покрывает
истинное значение прогноза
График 4
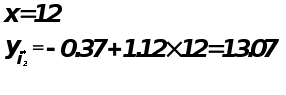
Оценка точности периода.
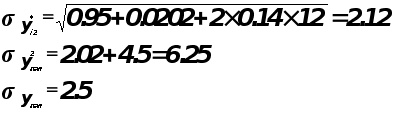
Построим доверительный интервал.
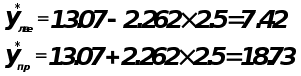
График 5
14
Похожие работы
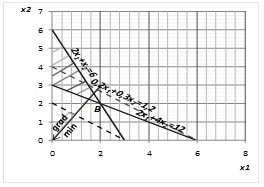
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...
... проверить знания студента из первой части курса, которая излагается в первых четырёх модулях. Во вторых вопросах билета проверяются знания классической предельной проблемы теории вероятностей и математической статистики, которые излагаются в следующих пяти модулях. 1. Вероятностная модель с не более чем счётным числом элементарных исходов. Пример: испытания с равновозможными исходами. 2. ...
... объектов; б) наличие данных за предыдущий период; в) наличие базисных данных; г) сопоставимость данных. 26. По характеру принимаемых решений экономический анализ подразделяется: а) предварительный, текущий и заключительный б) оперативный, ретроспективный и перспективный в) предварительный, последующий и итоговый 27. Информация, ...
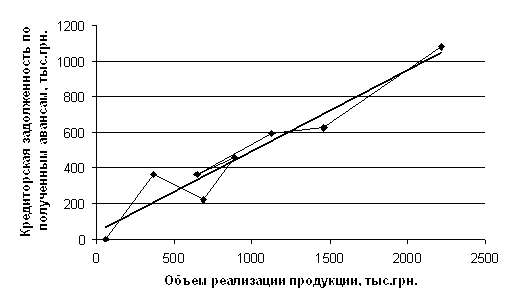
... можно прогнозировать динамику уровня кредиторской задолженности предприятия по полученным авансам при планировании изменения объемов реализации продукции на ОАО СЗКО «Молот». 3.5 Автоматизация анализа текущих обязательств Экономический анализ сопровождается выполнением большого объема разнообразных вычислений: абсолютных и относительных отклонений; средних величин; дисперсии; процентных ...
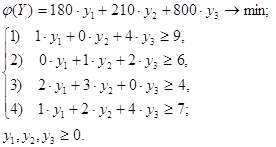
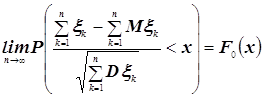
0 комментариев