sin^2(a)+cos^2(a)=1; |Sin Cos Tg tg(a)=sin(a)/cos(a); |++ -+ -+ tg(a)ctg(a)=1; |-- -+ +- 1+tg^2(a)=1/cos^2(a); | 1+ctg^2(a)=1/sin^2(a); |sin(p/2+-a)=cos(a); |sin(p+-a)=-+sin(a); sin(a+b)=sin(a)cos(b)+cos(a)sin(b); |sin(3p/2+-a)=-cos(a); sin(a-b)=sin(a)cos(b)-cos(a)sin(b); |sin(2p+-a)=+-sin(a); cos(a+b)=cos(a)cos(b)-sin(a)sin(b); | cos(a-b)=cos(a)cos(b)+sin(a)sin(b); |cos(p/2+-a)=+-sin(a); tg(a+b)=tg(a)+tg(b)/1-tg(a)tg(b); |cos(p+-a)=-cos(a); tg(a-b)=tg(a)-tg(b)/1-tg(a)tg(b); |cos(3p/2+-a)=+-sin(a); ctg(a+b)=ctg(a)ctg(b)-1/ctg(a)+ctg(b); |cos(2p+-a)=cos(a); ctg(a-b)=ctg(a)ctg(b)+1/ctg(b)-ctg(a); | |tg(p/2+-a)=-+ctg(a) sin(2a)=2sin(a)cos(a); |tg(p+-a)=+-tg(a) cos(2a)=cos^2(a)-sin^2(b)=1-2sin^2(a); |tg(3p/2+-a)=-+ctg(a) tg(2a)=2tg(a)/1-tg^2(a); |tg(2p+-a)=+-tg(a) ctg(2a)=ctg^2(a)-1/2ctg(a); | sin(3a)=3sin(a)-4sin^3(a); |ctg(p/2+-a)=-+tg(a) tg(3a)=3tg(a)-tg^3(a)/1-3tg^2(a); |ctg(p+-a)=+-ctg(a) ctg(3a)=3ctg(a)-ctg^3(a)/1-3ctg^2(a); |ctg(3p/2+-a)=-+tg(a) |ctg(2p+-a)=+-ctg(a) sin^2(a/2)=1-cos(a)/2; | cos^2(a/2)=1+cos(a)/2; | tg^2(a/2)=1-cos(a)/1+cos(a); | ctg^2(a/2)=1+cos(a)/1-cos(a); | tg(a/2)=sin(a)/1+cos(a)=1-cos(a)/sin(a); | ctg(a/2)=sin(a)/1-cos(a)=1+cos(a)/sin(a);| | sin(a)+sin(b)=2sin(a+b/2)cos(a-b/2); | sin(a)-sin(b)=2sin(a-b/2)cos(a+b/2); | cos(a)+cos(b)=2cos(a+b/2)cos(a-b/2); | cos(a)-cos(b)=-2cos(a+b/2)cos(a-b/2)= | =2cos(a+b/2)cos(b-a/2); | cos(a)+sin(b)=sqrt(2)cos(45-a); | cos(a)-sin(b)=sqrt(2)sin(45-a); | tg(a)+tg(b)=sin(a+b)/cos(a)cos(b); | tg(a)-tg(b)=sin(a-b)/cos(a)cos(b); | ctg(a)+ctg(b)=sin(a+b)/sin(a)sin(b); | ctg(a)-ctg(b)=sin(b-a)/sin(a)sin(b); | tg(a)+ctg(b)=cos(a-b)/cos(a)sin(b); | tg(a)-ctg(b)=-cos(a+b)/cos(a)sin(b); | tg(a)+ctg(a)=2/sin(2a); | tg(a)-ctg(a)=-2ctg(2a); | | sin(a)sin(b)=1/2(cos(a-b)-cos(a+b)); | cos(a)cos(b)=1/2(cos(a+b)+cos(a-b)); | sin(a)cos(b)=1/2(sin(a+b)+sin(a-b)); | | sin(a)=2tg(a/2)/1+tg^2(a/2); | cos(a)=1-tg^2(a/2)/1+tg^2(a/2); | tg(a)=2tg(a/2)/1-tg^2(a/2); | ctg(a)=1-tg^2(a/2)/2tg(a/2); |
Раздел:
Математика Количество знаков с пробелами: 1963
Количество таблиц: 0
Количество изображений: 0
... астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину. Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до ...
... носила чисто геометрический характер. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Постепенно тригонометрия органически вошла в математический анализ, механику, физику и технические дисциплины. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, ...
ыли
письменно
изложены греческим
астрономом
Гиппархом в
середине 2 века
до н.э. Наивысшими
достижениями
греческая
тригонометрия
обязана астроному
Птоломею (2 век
н.э.), создателю
геоцентрической
системы мира,
господствовавшей
до Коперника.
Греческие
астрономы не
знали синусов,
косинусов и
тангенсов.
Вместо таблиц
этих величин
они употребляли
таблицы: позволяющие
отыскать хорду
окружности
по ...
гралыПроизводныеТригонометрия


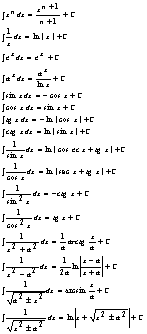
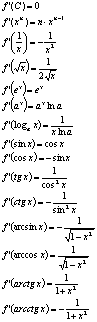
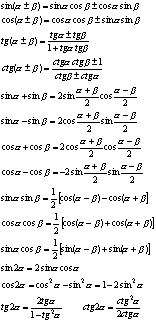
0 комментариев