Определитель произведения прямоугольных матриц. Теорема Коши-Бине

Курсовая работа

Выполнила студентка II курса группы ПМИ Решоткина Наталья Николаевна

Мурманский Государственный Педагогический Университет

Мурманск 2007

Введение

При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.

Цель данной работы: теоретическое обоснование и необходимость практического применения теоремы Коши-Бине:

Пусть , -  и -матрицы соответственно, и

Тогда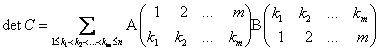

Другими словами, при  определитель матрицы  является суммой произведений всевозможных миноров порядка  в  на соответствующие миноры матрицы  того же самого порядка

Работа состоит из четырех глав, содержит заключение, список литературы и приложение программы для теоремы Коши-Бине. В главе I рассматриваются элементы линейной алгебры – матрицы, операции над матрицами и свойства сложения матриц, и умножения на скаляр. Глава II посвящается умножению матриц и его свойств, а также транспонирование произведения двух матриц. В главе III рассматриваются обратимые и элементарные матрицы. В главе IV вводиться понятие определителя квадратной матрицы, рассматриваются свойства и теоремы об определителях, а также приводится доказательство теоремы Коши-Бине, что является целью моей работы. В дополнение прилагается программа показывающая механизм нахождения определителя произведения двух матриц.

Глава I

§ 1 Определение, обозначения и типы матриц

Мы определяем матрицу как прямоугольную таблицу чисел:

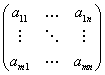
Где элементы матрицы aij (1≤i≤m, 1≤j≤n)-числа из поля .Для наших целей поле  будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы , где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.

Каждой  матрице  с элементами aij соответствует n×m матрица с элементами aji . Она называется транспонированной к  и обозначается через. Видно, что =. Строки матрицы  становятся столбцами в  и столбцы матрицы  становятся строками в.

Матрица называется нулевой если все элементы равны 0:

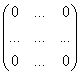
Матрица называется треугольной если все ее элементы, расположенные ниже главной диагонали равны 0

Треугольная матрица называется диагональной, если все элементы расположенные вне главной диагонали равны 0

Диагональной матрица называется единичной, если все элементы расположенные на главной диагонали равны 1

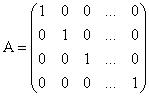
Матрица, составленная из элементов, находящихся на пересечении нескольких выбранных строк матрицы  и нескольких выбранных столбцов, называется субматрицей для матрицы . Если -номера выбранных строк и -номера выбранных столбцов, то субматрица это

В частности, строки и столбцы матрицы можно рассматривать как ее субматрицы.

§2 Операции над матрицами

Определим следующие операции:

Сумма двух  матриц , и  с элементами  и есть  матрица С с элементами , запишем это как

Произведение матрицы  на число поля есть матрица С с элементами , запишем как .

Произведение  матрицы на матрицу есть матрица С с элементами , запишем

 поле скаляров, рассмотрим 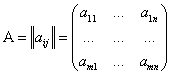, где элемент матрицы , расположенный в -строке , -столбце . Размерность матрицы .Если , то -квадратная матрица порядка . Множество -это множество всех  матриц над полем .

Опр. Две матрицы равны, если они имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы. Другими словами:  равна матрице , т.е

Опр. Пусть -это матрицы одинаковой размерности . Суммой матриц  и  называется матрица у которой в строке,  столбце расположен элемент , т.е. . Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:

Пример:

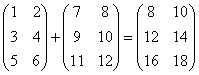
Опр. Пусть , , . Произведение скаляра  на матрицу  называется  у которой в строке,  столбце расположен элемент . Другими словами: Чтобы скаляр  умножить на матрицу  нужно все элементы матрицы  умножить на скаляр .

Определение. Противоположной к матрице  называется матрица

Свойства сложения и умножения матриц на скаляры:

-абелева группа

1) Сложение матриц  ассоциативно и коммутативно.

2)

3)

а)

б)

4)

Глава II

§1 Умножение матриц

,

,

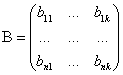
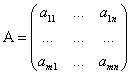Опр. Произведением  матрицы  на  матрицу  называется  матрица . , где

, где

Говорят, что  есть скалярное произведение -строки матрицы  на -столбец матрицы .

, где

Пример:

§2 Свойства умножения матриц

Умножение матриц ассоциативно:

1)  , если определены произведения матриц  и

Доказательство:

Пусть , так как определено , то  и определено , то

Определим матрицы:

а)

б)

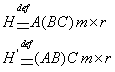 (1) матрицы, тогда  имеют одинаковую размерность

2) Покажем, что на одинаковых местах в матрицах  расположены одинаковые элементы

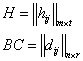из равенства (1) (2), (3). Подставляя (3) в (2) получим:

, тогда (4), (5). Подставляя (5) в (4) получим:

Вывод: Матрицы  имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.

Умножение матриц дистрибутивно :

Доказательство:

 так как определено , то  и определено , то

размерности

 размерности

Матрицы  имеют одинаковую размерность, покажем расположение одинаковых элементов:

,

,

Вывод: На одинаковых местах расположены одинаковые элементы.

3. , . Если определены  матрицы, то доказательство проводим аналогично свойству 2.

4. , : , если определена матрица

Доказательство:

 . Пусть ,

, ,

5. Умножение матриц в общем случае не коммутативно. Рассмотрим это на примере:

, тогда

§3 Техника матричного умножения

 поле скаляров, ,

Свойства:

Произведение  можно рассматривать, как результат умножения столбцов матрицы на  слева и как результат умножения строк матрицы  на  справа.

Пусть  матрица , -линейная комбинация столбцов матрицы  коэффициенты которой служат элементы матрицы

Пример

Пусть -матрица , тогда -линейная комбинация строк матрицы  коэффициенты которой служат элементы матрицы

Пример:

Столбцы матрицы -линейная комбинация столбцов матрицы . Строки -линейная комбинация строк матрицы .

§4 Транспонирование произведения матриц

 поле скаляров, , , ,

Теорема

 если , то . Обозначим: ,

Доказательство:

 1) Пусть ,

 - размерности ,- размерности , тогда и имеют одинаковую размерность

2) , -элемента расположенный в -строке, -столбце матрицы  т.е

, -произведение -строки транспонированной  на  столбец ,

Глава III

§1 Обратимые матрицы

 поле скаляров, множество матриц порядка

Определение. Квадратная матрица  порядка  называется единичной матрицей ,

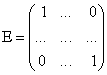
Пусть ,

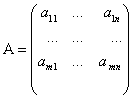
Теорема 1

, то для  выполняется  

Доказательство:

 

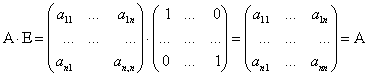
Из этого следует . Матрица  является единичной матрицей. Она выполняет роль единицы при умножении матриц.

Определение. Квадратная матрица называется обратимой если существует  так, что выполняются условия

Матрица  называется обратной к и обозначается , тогда если -это обратная к , то  обратная к -это взаимообратные матрицы т.е.

Теорема 2

Если -обратима, то существует только одна матрица обратная к

Доказательство:

 Пусть дана матрица , которая обратима и пусть существуют матрицы обратные к  т.е. . Имеем

Обозначение: Множество всех обратимых матриц порядка  над полем  обозначается

Теорема 3

Справедливы утверждения:

1)  алгебра

2)  группа

Доказательство:

1) -это бинарная операция

а) Пусть , так как -обратимые матрицы, проверим, что -это бинарная операция:

 обратные к

Аналогично: ,  обратимая матрица т.е -это бинарная операция

б) , матрица обратима, поэтому -это унарная операция

в)  обратима т.е

2) Докажем второе утверждение, что  группа. Для этого проверим аксиомы групп:

1)

2)

3)

 группа

Следствие:

Произведение обратимых матриц есть обратимая матрица

Если  обратима, то обратима

§2 Элементарные матрицы

Пусть  поле скаляров

Определение.Элементарной матрицей называется матрица, полученная из единичной матрицы  в результате одного из следующих элементарных преобразований:

Умножение строки (столбца)  на скаляр

Прибавление к какой либо строке (столбцу)  другой строки (столбца), умноженный на скаляр

Обозначение: -элементарная матрица, полученная умножением на  -строки (столбца) матрицы

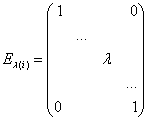
-строка

-элементарная матрица, полученная прибавлением к -строке (столбцу) матрицы  -строки (столбца), умноженной на

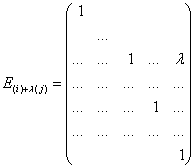
-строка

Пример: Элементарные матрицы порядка 2

, , , ,

Обозначение: -элементарная матрица, полученная из единичной матрицы с помощью элементарного преобразования

Глава IV

§1 Определители

Определитель матрицы обозначается . Другими словами определитель матрицы -это сумма произведений из множества  умноженная на знак, соответствующей подстановки.

Пример

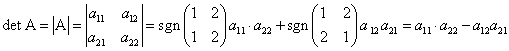
Определитель второго порядка равен произведению элементов главной диагонали вычесть произведение элементов на побоичной.

Для

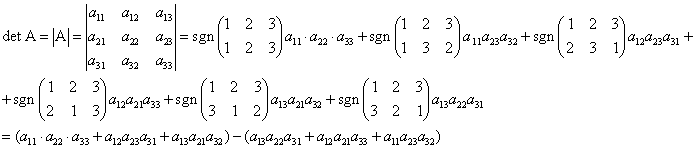
Получили правило треугольника:

§2 Простейшие свойства определителей

Определитель матрицы с нулевой строкой (столбцом) равен нулю

Определитель треугольной матрицы равен произведению элементов, расположенных на главной диагонали

-это треугольная матрица если элементы под главной диагональю равны нулю.

Определитель диагональной матрицы равен произведению элементов, расположенных на главной диагонали. Матрица  диагональная если все элементы, расположенные вне главной диагонали равны нулю.

§3 Основные свойства определителей

 поле скаляров,

1)

Доказательство:

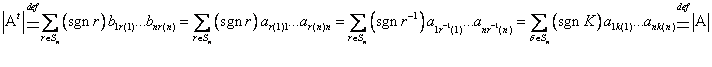, обозначим . Если  «пробегает» все множество , то тоже «пробегает» все т.е.

При перестановке двух столбцов (строк) матрицы ее определитель изменит знак.

Доказательство:

I) Перестановка столбцов:

Пусть - это матрица, полученная из  перестановкой двух столбцов с номерами , где . Рассмотрим транспозицию:

, транспозиция является нечетной подстановкой , ,

В доказательстве будем использовать равенство:

 

Если  пробегает все множество значений , то тоже пробегает все значения и

II) Перестановка строк

Пусть  получена из перестановкой двух строк, тогда  получена из  перестановкой двух столбцов, тогда

III) Определитель матрицы, имеющий две одинаковые строки (столбца) равных нулю

Доказательство:

Проведем для такого поля , где

Замечание

Доказательство для случая найди в учебнике Куликовой Алгебра и теория чисел

Пусть в  есть две одинаковые строки с номерами и , где , поменяем местами строки и , получим матрицу

(по св.2)

 и , тогда

Если у  два одинаковых столбца, то у транспонированной матрицы  две одинаковые строки

IV) Если все элементы какой-либо строки (столбца) матрицы  умножить на , то определитель умножиться на

Доказательство:

Пусть  получена из  умножением на  строки

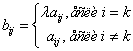
 так как , то

Аналогичное доказательство для столбцов

V) Определитель матрицы у которой две строки (столбца) пропорциональны равны нулю

Доказательство:

Пусть в матрице ,  строки  пропорциональны т.е -строка равна произведению  на -строку. Пусть

Для столбцов:

Пусть  получена из , . Столбцы  и  пропорциональны и

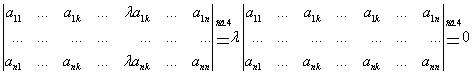
VI) Если каждый элемент -строки(столбца) квадратной матрицы  есть сумма двух элементов, то определитель  равен сумме двух определителей. В матрице первого определителя в - строке (столбце), записаны первые слагаемые, а в матрице второго определителя вторые слагаемые. Остальные элементы матриц этих определителей такие же как у матрицы

Доказательство:

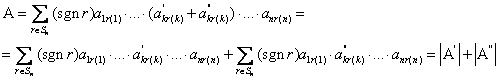
VII) Ели к какой либо строке (столбцу) матрице определителя прибавить другую строку (столбец), умноженный на , то определитель неизменится.

Доказательство:

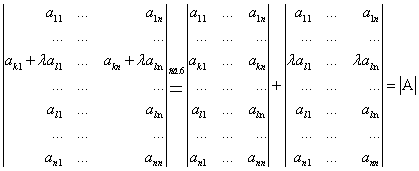
Для столбцов анологично.

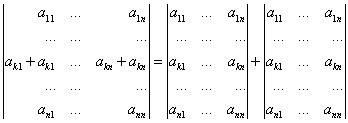
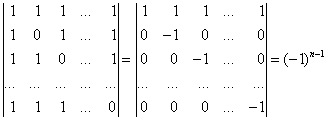
VIII) Если какая либо строка (столбец) матрицы  является линейной комбинацией других строк (столбцов) , то определитель

Доказательство:

Если какая то строка линейная комбинация других строк, то к ней можно прибавить другие строки, умноженные на скаляры так, чтобы получилась нулевая строка. Определитель такой матрицы равен нулю.

Пример:

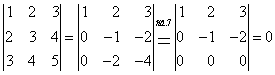 (сначала умножаем первую строку на -2 и складываем со второй, затем на -3 и складываем с третей). Такое правило приведения к треугольному виду используется для определителей - порядка:

 так как определитель треугольной матрицы равен произведению элементов расположенных на главной диагонали.

Если квадратная матрица является произведением некоторых матриц (которые могут быть прямоугольными), то часто бывает важно иметь возможность выразить определитель произведения в терминах свойств множителей. Следующая теорема –мощный показатель этого.

§4 Миноры и алгебраические дополнения.

Теоремы об определителях.

 поле скаляров,

Опр. Минор  элемента  определителя  порядка - определитель порядка , полученный из  вычеркиванием -строки и -столбца.

Главные миноры определителя

Для 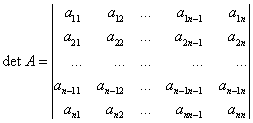 главные миноры есть определители

, , …, ,

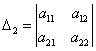Пример:

Рассмотрим матрицу 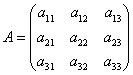 и вычислим ее миноры : , ,

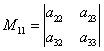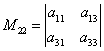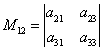
Определение. Алгебраическим дополнением элемента  обозначается  называется число

Пример: Вычислим , ,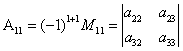

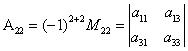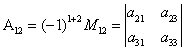
Лемма 1

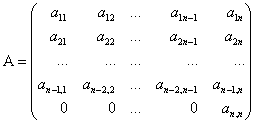и.

Доказательство:

 (в сумме только те слагаемые ненулевые, где )

Тогда подстановка имеет вид: 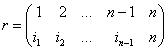, где . К подстановке  поставим в соответствие  т.е  

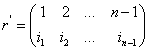, такое соответствие называется взаимооднозначным отображением множества подстановок  на множество подстановок , . Очевидно, что и  имеют одинаковые инверсии, значит  имеют одинаковую четность и знаки

Лемма 2

Если равны нулю все элементы какой-либо строки (столбца) матрицы  за исключением быть может одного элемента, то определитель матрицы  равен произведению этого элемента на его алгебраическое дополнение

Доказательство:

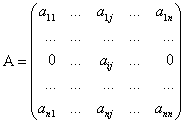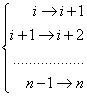Пусть все элементы -строки матрицы  за исключением элемента ,  перестановкой строк и столбцов  переместили элемент  в правый нижний угол , значит  строк и -столбцов. Знак будет меняться раз, после этого получиться матрица у которой все элементы последней строки кроме может быть  равны нулю. По Лемме 1 , т к

Теорема Лагранжа

 равна сумме произведений элементов какого-либо столбца (строки) матрицы  на их алгебраическое дополнение. Другими словами: разложение по -столбцу матрицы  имеет вид: , а разложение по -строке матрицы :

Доказательство:

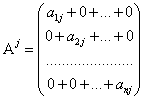рассмотрим -столбец матрицы  и запишем в виде: , по 6 свойству определителей:

, аналогично доказывается формула разложение по -строке матрицы .

Теорема 2

Справедливы равенства:

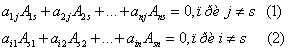
Рассмотрим матрицу , которая получена из матрицы  следующим образом: все столбцы матрицы , кроме -го такие же как и у матрицы . -тый столбец матрицы  совпадает с -столбцом , тогда у  два одинаковых столбца, поэтому определитель матрицы  равен нулю, разложим определитель матрицы  по -тому столбцу.

, , тогда . Формула (2) показывается аналогично.

Следствие:

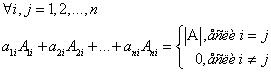
§5 Определитель произведение матриц

 поле скаляров, ,

Лемма 1

Пусть  элементарная матрица порядка , тогда справедливо равенство:

1) ., т.е  получена из матрицы , умножением -строки на скаляр . Определитель матрицы .

Матрица  получена из  умножением -строки на скаляр , поэтому определитель

2)

Матрица, полученная из  прибавлением к -строке

Лемма 2

-элементарные матрицы

1) , доказательство следует из Леммы 1

2) , доказательство из утверждения (1) при условии

Теорема 1

Определитель произведения двух матриц равен произведению их определителей т.е.

Доказательство:

Пусть строки матрицы  линейно независимы, тогда существует цепочка элементарных преобразований 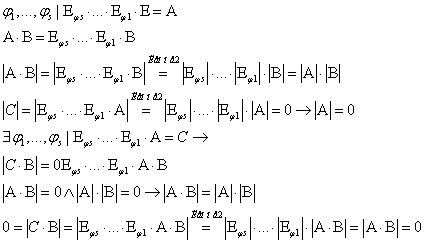, тогда по Лемме 2 следует, что . Из того, что () имеем: , тогда

2) Строки  линейно зависимы, тогда существует цепочка элементарных преобразований, которая переводит  в ступенчатую матрицу , у которой есть нулевая строка т.е. , . Тогда

Из того, что , в произведении , тоже есть нулевая строка, потому

Необходимые и достаточные условия равенства определителя нулю

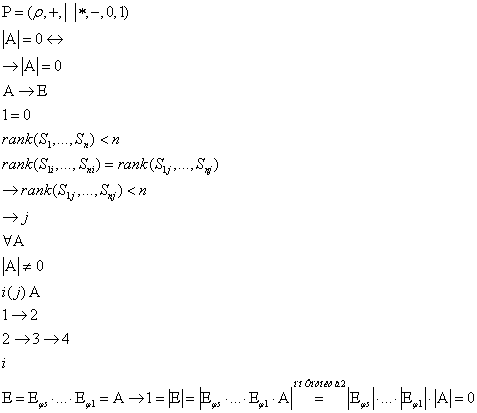 поле скаляров, ,-матрица над полем

Теорема 1

строки (столбцы) матрицы линейно зависимы

Достаточность:

Если строки (столбцы) матрицы линейно зависимы, то какая-то строка является линейной комбинацией других строк (по 8 свойсву определителей)

Необходимость:

Пусть . Докажем, что строки линейно зависимы. Предположим, что строки  линейно независимы, тогда существует цепочка элементарных преобразований переводящее . Из доказанного в пункте II следует, что . Получили противоречье . Докажем, что если -строка матрицы  линейно зависима,, но (числа векторов столбца)  линейно зависима.

Теорема 2

 следующие условия равносильны:

1)

2) -линейно зависимы

3) -обратима

4)  представима в виде произведения элементарных матриц

Доказательство:

 доказано в Теореме 1

§6 Разбиение матриц

Если  матрицу ,  матрицу ,  матрицу  и  матрицу  записать в виде

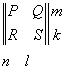
 (1)

То они, образуют некоторую  матрицу . В таком случае  могут быть названы блоками матрицы . И обозначены  соответственно. Представление (1) называется разбиением матрицы .

Если матричное произведение существует и , разбиты на блоки , , а разбиение по столбцам матрицы  соответствует разбиению по строкам матрицы , то можно ожидать, что  имеет блоки , задаваемые формулой

Таким образом, мы предполагаем, что произведение матриц в терминах блоков, полученных при соответствующих разбиениях сомножителей, формально совпадает с произведением этих матриц в терминах скалярных элементов. Покажем это на примере:

Упражнение1. Пусть

, ,

, ,

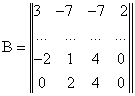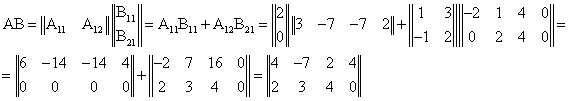
Это проверяется прямым вычислением

Теорема (1)

Пусть матрица  из  имеет блоки , где матрица, , и  матрица из  с блоками размера . Тогда  имеет блоки

Доказательство. Отметим, что каждое произведение существует и является  матрицей. Следовательно,  существует и будет  матрицей. Для фиксированного каждое  имеет  столбцов и для фиксированного  каждое  имеет строк, откуда следует, что блоки некоторой  матрицы .

Пусть некоторый элемент матрицы , расположенный в клетке  блока . Так как , есть сумма элементов в клетках и матриц , . Но элемент матрицы в клетке  является суммой произведений элементов в строке матрицы  на элементы столбца матрицы . Далее, элементы строки матрицы  совпадают с некоторыми элементами  строки в , а именно, с , где индекс  определяется неравенствами

, если

, если

Элементы столбца матрицы будут элементами  в . Следовательно,

Мы определили миноры порядка  для  определителя. В общем случае, если из -матрицы выбросить все строки, кроме строк , и все столбцы, кроме столбцов , то определитель полученной в результате матрицы называется минором матрицы  порядка , то

Миноры, для которых , называются главными для матрицы . Если  -  матрица, то  и алгебраическое дополнение , например, есть

Если квадратная матрица является произведением некоторых матриц (которые могут быть прямоугольными), то иногда важно выразить определитель произведения в терминах свойств сомножителей. Следующая теорема - мощный результат этого рода.

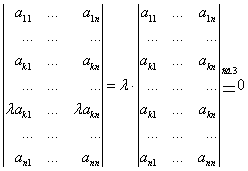
§7 Теорема (формула Бине-Коши)

Теорема (формула Бине-Коши)

Пусть , -  и -матрицы соответственно, и

Тогда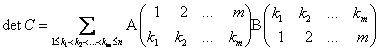

Другими словами, при  определитель матрицы  является суммой произведений всевозможных миноров порядка  в  на соответствующие миноры матрицы  того же самого порядка.

Упражнение1. Покажем на примере

Пусть , , 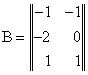 и , тогда по формуле Коши-Бине:

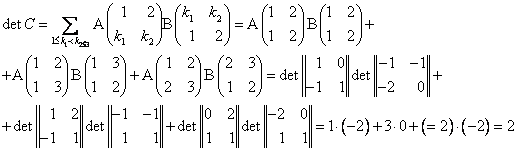
Доказательство теоремы:

Так как , то можно записать

Определитель-это аддитивная и однородная функция каждого из своих столбцов. Используя этот факт для каждого из  столбцов в , выражаем  в виде суммы  определителей:

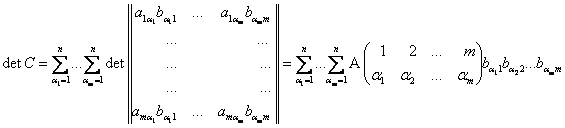
Те члены в суммировании, которые имеют совпадающие два или более индексов , равны нулю, так как в этих случаях миноры будут иметь по крайней мере два совпадающих столбца. Таким образом, нужно рассматривать лишь те  членов суммирования, в которых индексы  различны. Мы распределяем эти остающиеся члены на  групп по  членов в каждой таким образом, чтобы в каждой группе члены отличаются лишь порядком индексов . Отметим также, что можно написать

, где . Следовательно, сумма по  членам, в которых -перестановка чисел , задается выражением: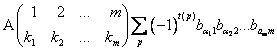

Переставляя элементы  так, чтобы первые индексы в возрастающем порядке, приводим это выражение к виду:

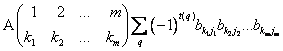
где -перестановка  чисел , как очевидно . Из определителя функции определителя теперь следует, что это выражение есть просто:

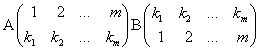
Следствие. Определитель произведения двух кратных матриц равен произведению определителй множителей.

Это следует из Теоремы при

Заключение

В данной работе рассмотрена основная теория матриц и доказательство теоремы Коши-Бине. Также представлено применение данной теоремы при нахождении определителя произведения двух прямоугольных матриц в программе написанной на языке программирования Дельфи с возможностью ввода матриц вручную и подгрузкой из файла.

Данная теорема Коши-Бине:

Пусть , -  и -матрицы соответственно, и

Тогда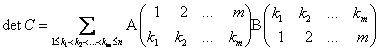

На примере можно рассмотреть работу программы реализующей алгоритм нахождения определителя прямоугольных матриц на основе формулы Коши-Бине.

Будем искать миноры 2 порядка:

1)

Пусть A m = 2 n = 3

1 0 2

-1 1 1

B m = 3 n = 2

-1 -1

-2 0

1 1

получаем матрицу C m = 2 n = 2

1 1

0 2

Итого: Det C = 2

2)

Переборы:

1A) 1 2

1 0

-1 1

DetA = 1

1B) 1 2

-1 -1

-2 0

DetB = -2

2A) 1 3

1 2

-1 1

DetA = 3

2B) 1 3

-1 -1

1 1

DetB = 0

3A) 2 3

0 2

1 1

DetA = -2

3B) 2 3

-2 0

1 1

DetB = -2

C = (1)*(-2) + (3)*(0) + (-2)*(-2)

Итого по формуле Коши - Бине: 2

Данная программа наглядно показывает нахождение миноров порядка m, где m-это количество строк в матрице .

Список литературы

1. Гантмахер Ф.Р. Теория матриц. – 4-е изд. – М.: Наука. Гл.ред. физ. – мат. мет., 1988. с. 13-32.

2. Фаддеев Д.К. Лекции по алгебре.- М.:Наука. Гл.ред. физ. – мат. мет., 1984.-с.216.

3. Курош А.Г. Курс высшей алгебры. – 14 - е изд. - Спб.: Лань, 2005. -с.322

4. Ланкастер П. Теория матриц– М.: Наука. Гл.ред. физ. – мат. мет., 1973, с.17-44

5. Маркус М., Минк Х. Обзор по теории матриц и матричных неравенств. – М.: Наука. Гл.ред. физ. – мат. мет. , 1972, с.232

6. Большакова И.В. Высшая математика - Учебное издание, 2003, с.5-10

Приложение

Внешний вид программы:

Исходный код:

unit MainUnit;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Menus, Math, cdet;

Const

MaxN = 10; //Максимальное число столбцов в массиве

MaxM = 10; //Максимальное число строк в массиве

DefValueMas = 3; //Значение по умолчанию (размерность)

type

TVS_MAssPerebor = Array of Real; //Массив переборов

TVS_Mass = array of array of Real; //Описали 2х мерный динамический массив

TVS_MassData = Record //Создаем запись - массив, в котором:

Mass : TVS_Mass ; //Массив

M, //Строки массива

N : Integer; //Столцы массива

Name : Char; //Название матрицы для вывода информации (A, B, C)

end; {TVS_MassData = Record}

TMainForm = class(TForm)

MainMenu1: TMainMenu;

N1: TMenuItem;

NMultiplication: TMenuItem;

N2: TMenuItem;

InputMassB: TMenuItem;

N3: TMenuItem;

N4: TMenuItem;

nDetA: TMenuItem;

NDetB: TMenuItem;

ResultMemo: TMemo;

N5: TMenuItem;

DetC: TMenuItem;

nmbn1: TMenuItem;

N6: TMenuItem;

N7: TMenuItem;

N8: TMenuItem;

N9: TMenuItem;

N10: TMenuItem;

OpenDialog: TOpenDialog;

procedure InputMassAClick(Sender: TObject);

procedure NMultiplicationClick(Sender: TObject);

procedure VS_MultiplicMass (Var inMassA, InMassB, MassOut : TVS_MassData);

procedure InputMassBClick(Sender: TObject);

procedure VS_InputMass(Var InMass : TVS_MassData);

procedure VS_ShowMass (inCaption : String; inMass: TVS_MassData);

procedure FormShow(Sender: TObject);

procedure N3Click(Sender: TObject);

procedure nDetAClick(Sender: TObject);

function VS_Det(InMass : TVS_MassData): Real;

procedure NDetBClick(Sender: TObject);

procedure VS_ShowMassToMemo(Caption : String; InMass : TVS_MassData; ShowRazm : Boolean = True);

procedure N5Click(Sender: TObject);

procedure DetCClick(Sender: TObject);

Procedure AssignMass(InMAss : TVS_MassData; Var OutMass : TVS_MassData);

Procedure VS_VerMass(Var Massin1, MAssIn2: TVS_MassData);

Procedure VS_LoadData(Var InMAss : TVS_MassData);

Procedure VS_GetRazmOnFile(FileName : String; Var Col, Row : Integer);

Function VS_GetColOnFile(InStr: String): Integer;

//Миноры

function VS_Minor(II, Jj: Integer; InMass : TVS_MassData): REal;

Procedure VS_InitMassInStr(InStr: String; CurRow : Integer; Var InMass: TVS_MassData);

Procedure VS_InitMassPErebor;

Procedure VS_Init2xMassPerebot;

Procedure VS_SortMassPerebor;

Procedure VS_GetMAssForDet;

Function VS_IfMassEq(Massin1, MAssIn2: TVS_MassData) : Boolean;

Function VS_GetKoshi_Bine : Real;

procedure VS_GenerateColMinorData(CurCol, Col : Integer; Var inMass : TVS_MassData);

procedure VS_GenerateRowMinorData(CurCol, Col : Integer; Var InMass : TVS_MassData);

Procedure VS_MinorMass(InMass : TVS_MassData; Var OutMass : TVS_MassData);

procedure N6Click(Sender: TObject);

procedure N7Click(Sender: TObject);

procedure N8Click(Sender: TObject);

procedure lll1Click(Sender: TObject);

procedure N9Click(Sender: TObject);

procedure N10Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

MainForm: TMainForm;

MassP : TVS_MAssPerebor;

MassPer,

MassA,

MassB, MassC : TVS_MassData;

DetB,

DetA : TVS_MAssPerebor; //Массив детерминант А

implementation

uses InRazmUnit, InMassUnit;

{$R *.dfm}

function TMainForm.VS_Det(InMass : TVS_MassData): Real;

var

Temp, A: TVS_MassData;

Cols, Rows, Count: Word;

i, j, k: Integer;

begin

Result := 1; //Результат функции по умолчанию

If InMass.N <> InMass.M Then Exit; //если матрица не квадратная - уходим, так как решение методом диагонали

Count := InMass.M ; // Получили размерность исходного массива

SetLength(A.Mass, Count, Count);//Установили размер матрицы

SetLength(Temp.Mass, 1, Count); //Установили размер мартицы

AssignMass(InMass, A); //Во временный массив заносим данные из исходного, чтобы не портить исходный массив

//Поиск и решение

for i := 0 to Count - 2 do {Начало преобразования к верхнему треугольному виду}

begin

for j := i to Count - 1 do {* Поиск }

begin {* нулевых }

Rows := 0; {* строк }

Cols := 0; {* и }

for k := i to Count - 1 do {* столбцов }

begin {* в }

Rows := Rows + Ord(A.Mass[j, k] = 0); {* матрице }

Cols := Cols + Ord(A.Mass[k, j] = 0); {* }

end;{for k := i to Count - 1 do} {* }

if Rows + Cols = 0 then {* }

Break; {* }

if (Cols = Count - i) or (Rows = Count - i) then {* }

begin {* }

Result := 0; {* }

Exit {* }

end {if (Cols = Count - i) or (Rows = Count - i) then }

end; {for j := i to Count - 1 do } {* }

if A.Mass[i, i] = 0 then

for j := i + 1 to Count - 1 do

if A.Mass[j, i] <> 0 then

begin

Result := -Result; {* меняем строку }

Temp.Mass[0] := A.Mass[i]; {* на строку с }

A.Mass[i] := A.Mass[j]; {* первым }

A.Mass[j] := Temp.Mass[0]; {* ненулевым }

Break {* элементом }

end;

for j := i + 1 to Count - 1 do

if A.Mass[j, i] <> 0 then

begin

for k := i + 1 to Count - 1 do

A.Mass[j, k] := A.Mass[j, k] - A.Mass[i, k] * A.Mass[j, i] / A.Mass[i, i];

A.Mass[j, i] := 0

end

end; {Конец преобразования}

for i := 0 to Count - 1 do { Определитель как произведение }

Result := Result * A.Mass[i, i]; { элементов на главной диагонали}

end;

procedure TMainForm.InputMassAClick(Sender: TObject);

begin

If InRazmForm = Nil Then Application.CreateForm(TInRazmForm, InRazmForm);

With InRazmForm do

Begin

Caption := 'Ввод размерности ряда А';

Hint := Caption; //

ShowHint := True; //Разрешаем быстрые подсказки

lbPrompt1.Caption := 'Размерность N ';

//Настройка эелемента ввода для размерности массива по строкам - М

sedtRazmA.MinValue := 1; //Установили минимальное знаечение для ввода-переключателя

sedtRazmA.MaxValue := MaxN ; //Установили максимальное значение для ввода - переключателя

sedtRazmA.Value := MassA.N; //Установили значение, выводимое на экран

//Настройка эелемента ввода для размерности массива по столбцам - N

sedtRazmB.MinValue := 1; //Установили минимальное знаечение для ввода-переключателя

sedtRazmB.MaxValue := MaxM; //Установили максимальное значение для ввода - переключателя

sedtRazmB.Value := MassA.M; //Установили значение, выводимое на экран

lbPrompt2.Caption := 'Размерность M ';

btnNext.Caption := 'Далее';

btnCancel.Caption := 'Отмена';

If InRazmForm.ShowModal = Mrok Then //если пользователь нажал кнопку "Далее"

Begin

MassA.N := sedtRazmA.Value; //Сохраняем размерность массива

MassA.M := sedtRazmB.Value; //Сохраняем размерность массива

VS_InputMass(MassA); //Выводим сетку для ввода масива

end; {If ShowModal = Mrok Then}

end; {With InRazmForm do}

end; {procedure TMainForm.InputMassAClick(Sender: TObject);}

procedure TMainForm.NMultiplicationClick(Sender: TObject);

//Умножение матриц

begin

VS_MultiplicMass(MassA, MassB, MassC); //Умножаем матрицы

VS_ShowMassToMemo('Результат произведения A*B получился ', MassC); //Результат выводим в Мемо

VS_ShowMass('Итоговый результат ', MassC); //Выводим результаты расчета

end;

procedure TMainForm.VS_MultiplicMass(var inMassA, InMassB, MassOut: TVS_MassData);

//Умножаем матрицы

//N, M - размерность матрицы, где

//N - стоблец

//M - строка

//inMassA - массив А

//inMassB - массив Б

//MassOut - массив С / выходной массив

Var P, i, j : Integer;

S : Real;

begin

For I := 0 to inMassA.M - 1 do // i = 1.. m

For J := 0 to inMassB.N - 1 do // j = 1.. k

begin

S := 0; //Сбнуляем счетчик

For P := 0 to inMassA.N -1 do // p = 1..n

S := S + inMassA.Mass[i, p] * InMassB.Mass[p, j]; //Вычисляем по формуле (Cij = Ep (Aip *Bpj)? где i=1..m, j = 1..k)

MassOut.Mass[I, J] := s; //Сохраняем результат в массив С

end;

MassOut.N := inMassB.N; //Сохраняем получившиюся размерность массива С

MassOut.M := inMassA.M; //Сохраняем получившиюся размерность массива С

end;

procedure TMainForm.InputMassBClick(Sender: TObject);

begin

If InRazmForm = Nil Then Application.CreateForm(TInRazmForm, InRazmForm);

With InRazmForm do

Begin

Caption := 'Ввод размерности ряда Б';

Hint := Caption;

ShowHint := True; //Разрешаем быстрые подсказки на форме

lbPrompt1.Caption := 'Размерность N ';

sedtRazmA.MinValue := 1; //Установили минимальное знаечение для ввода-переключателя

sedtRazmA.MaxValue := MaxN; //Установили максимальное значение для ввода - переключателя

sedtRazmA.Value := MassB.N; //Установили значение, выводимое на экран

sedtRazmB.MinValue := 1; //Установили минимальное знаечение для ввода-переключателя

sedtRazmB.MaxValue := MaxM; //Установили максимальное значение для ввода - переключателя

sedtRazmB.Value := MassB.M; //Установили значение, выводимое на экран

lbPrompt2.Caption := 'Размерность M ';

btnNext.Caption := 'Далее';

btnCancel.Caption := 'Отмена';

If ShowModal = Mrok Then //если пользователь нажал "Далее"

Begin

MassB.N := sedtRazmA.Value; //Сохраняем размерность массива

MassB.M := sedtRazmB.Value; //Сохраняем размерность массива

VS_InputMass(MassB); //Выводи окно с сеткой для ввода массива

end{If ShowModal = Mrok Then}

end; {With InRazmForm do}

end;

procedure TMainForm.VS_ShowMass(inCaption : String; inMass: TVS_MassData);

//Выводим массив

//N, M - размерность матрицы, где

//N - стоблец

//M - строка

//inMass - массив, который выводим

Var

I, K : Integer;

begin

If InMassForm = Nil Then Application.CreateForm(TInMassForm, InMassForm);

with InMassForm do

Begin

Caption := 'Вывод массива';

strGrid.RowCount := InMass.M+1;

strGrid.ColCount := inMAss.N+1;

For I := 0 To inMAss.N -1 do //Выводим шапку для столбцов

strGrid.Cells[I + 1, 0] := 'N = ' + IntToStr( I + 1);

For I := 0 To inMAss.M -1 do //Выводим шапку для строк

strGrid.Cells[0, I + 1] := 'M = ' + IntToStr( I + 1);

btnNext.Caption := 'Ok';

btnCancel.Visible := False; //Выключаем кнопку "Отмена". Она нам не нужна

For I := 0 To inMAss.N -1 do //Пробегаемся по строкам

For K := 0 To inMAss.M -1 do //Пробегаемся по столбцам

InMassForm.strGrid.Cells[I +1,K +1] := FloatToStr(inMass.Mass[K, I]); //Выводим в сетку ранее сохраненный массив

ShowModal; //Выводим окно, ждем реакции пользователя

btnCancel.Visible := True; //Не забываем включить кнопку "Отмена", иначе ее не увидят в других нужных нам метсах

end; {with InMassForm do}

End;

procedure TMainForm.FormShow(Sender: TObject);

//Обрабатываемся прри вызове формы

Var I, J : Integer;

begin

//Обнуляем массивы, во избежание шаманских действий программы

SetLength(MassA.Mass, MaxM , MaxN ); //Установили размер массива в памяти

SetLength(MassB.Mass, MaxM , MaxN ); //Установили размер массива в памяти

SetLength(MassC.Mass, MaxM , MaxN ); //Установили размер массива в памяти

For I := 0 to MaxM - 1 Do //Пробегаемся по строкам

For J := 0 to MaxN - 1 do //Пробегаемся по столбцам

Begin

MassA.Mass[I, J] := 0;

MassB.Mass[I, J] := 0;

MassC.Mass[I, J] := 0;

end; {For J := 1 to MaxN do}

//Обнуляем переменные размерностей массивов

MassA.N := DefValueMas; //Устанавливаем размерность матрицы по умолчанию

MassA.M := MassA.N;

MassB.N := MassA.N;

MassB.M := MassA.N;

MassC.N := MassA.N;

MassC.M := MassA.N;

MassA.Name := 'A';

MassB.Name := 'B';

MassC.Name := 'C';

ResultMemo.Clear; //Очищаем Мемо-поле.

end;

procedure TMainForm.VS_InputMass(var InMass: TVS_MassData);

//Вводим Элементы массива

Var

I, K : Integer;

begin

If InMassForm = Nil Then Application.CreateForm(TInMassForm, InMassForm);

with InMassForm do

Begin

Caption := 'Ввод массива';

strGrid.RowCount := InMass.M+1; //указали количество строк рамным М

strGrid.ColCount := InMass.N+1; //Указали количество столбцов, равным N

For I := 0 To InMass.N -1 do //Делаем шапку для столбцов

strGrid.Cells[I +1, 0] := 'N = ' + IntToStr( I +1);

For I := 0 To InMass.M -1 do //Делаем шапку для строк

strGrid.Cells[0, I +1] := 'M = ' + IntToStr( I +1);

//Заносим результаты массива в сетку, если вводили ранее

For I := 0 to InMass.M -1 do //Пробегаемся по строкам массива

For K := 0 to InMass.N -1 do //Пробегаемся по столбцам массива

Try

strGrid.Cells[I+1, K+1] := FloatToStr (InMass.Mass[K, I]); //Выводим массив в сетку

except

strGrid.Cells[I+1, K+1] := '0';

end;

btnNext.Caption := 'Далее';

btnCancel.Caption := 'Отмена';

If ShowModal = Mrok Then //Выводим форму, ждем реакции пользователя

Begin

SetLength(MassA.Mass, InMass.M +1 , InMass.N +1); //Установили размер массива в памяти

For I := 0 To InMass.N -1 do //Пробегаемся по строкам массива

For K := 0 To InMass.M -1 do //Пробегаемся по столбцам массива

Try //Включаем обработку ошибок

InMass.Mass[K, I] := StrToInt(InMassForm.strGrid.Cells[I +1,K +1]); // Заносим элемент из сетки в массив

except //Если произошла ошибка, например с переводом строки в число

InMass.Mass[I, K] := 0; //Если ошибка - заносим в массив 0

end; {except}

VS_ShowMassToMemo('Успешно введена матрица ',InMass); //Выводим матрицу в Мемо

end;{If ShowModal = Mrok Then}

end;

end;

procedure TMainForm.N3Click(Sender: TObject);

//Выводим результат. Просто выводим массив

begin

VS_ShowMass('', MassC)

end;

procedure TMainForm.nDetAClick(Sender: TObject);

//Определяем определитель матрицы А

Var Det : Real;

begin

Det := VS_Det(MassA); //ВЫчисляем определитель

ResultMemo.Lines.Add('Определитель матрицы А равен ' + FloattoStr(Det)); //Выводим результат в Мемо

ShowMessage(FloatToStr(Det)); //Выводим результат в диалоговое окно

end;

procedure TMainForm.NDetBClick(Sender: TObject);

//Определяем определитель матрицы B

Var Det : Real;

begin

Det:= VS_Det(MassB); //Вычисляем определитель

ResultMemo.Lines.Add('Определитель матрицы B равен ' + FloattoStr(Det)); //Результат вычислений выводим в МЕмо

ShowMessage(FloatToStr(Det)); //Результат выводим в диалоговое окно

end;

procedure TMainForm.VS_ShowMassToMemo(Caption : String; InMass: TVS_MassData; ShowRazm : Boolean = True);

//Выводим массив в МЕмо

Var S : String;

I, J : Integer;

begin

If ShowRazm Then ResultMemo.Lines.Add(Caption + InMass.Name + ' m = ' + IntToStr(InMass.M) + ' n = ' + IntToStr(InMass.n))

Else ResultMemo.Lines.Add(Caption );

For I := 0 to InMass.M - 1 do //Пробегаемся по строкам

Begin

S := ''; //Готовимся к формированию строки

For J := 0 To InMass.N -1 Do //Пробегаемся по столбцам

S := S + FloatToStr(InMass.Mass[i,j]) + ' '; //Формируем строку элементов

ResultMemo.Lines.Add(S); //Выводим строку в Мемо

end;{For I := 0 to InMass.M - 1 do //Пробегаемся по строкам}

end;

procedure TMainForm.N5Click(Sender: TObject);

Var DetA, DetB, Det : Real;

begin

ResultMemo.Clear;

//Решаем det C обычным способом

VS_VerMass(MAssA, MAssB); //Проверяем массивы. Если в первом массиве число столбцов меньше, чем во втором, меняем матрицы местами

ResultMemo.Lines.Add('1)');

VS_ShowMassToMemo('Пусть ', MassA); //Выводим матрицу А

VS_ShowMassToMemo('', MassB); //Выводим матрицу Б

VS_MultiplicMass(MassA, MassB, MassC); //Умножаем матрицы

VS_ShowMassToMemo('получаем матрицу ', MassC); //Выводим матрицу С

Det := VS_Det(MassC);

ResultMemo.Lines.Add('Итого: Det C = ' + FloatToStr(Det));

ResultMemo.Lines.Add('2)');

//Решаем по Бине-Коши

If (MassA.M > MassA.N) Then

Begin //попали под условие, когда М>n , значит определитель равен 0

ResultMemo.Lines.Add('m > n массива А , исходя из т. Бине - Коши, DetC = 0');

Exit //Завершаем процедуру

end;

//If (MassB.M > MassB.N) Then

// Begin //попали под условие, когда М>n , значит определитель равен 0

// ResultMemo.Lines.Add('m > n массива B , исходя из т. Бине - Коши, DetC = 0');

// Exit//Завершаем процедуру

// end;

If (MassA.M = MassA.N) And (MassA.M = MassA.N)

Then //попали под условие, когда обе матрицы кувадратные

Begin

ResultMemo.Lines.Add('m = n массивов B и А, исходя из т. Бине - Коши, ');

DetA := VS_Det(MassA);

DetB := VS_Det(MassB);

Det := DetA * DetB;

ResultMemo.Lines.Add('DetC = detA * Det B = ' + FloatToStr(DetA) + ' * ' + FloatToStr(DetB) + ' = ' + FloatToStr(Det));

end;

If (MassA.M < MassA.N) And (MassB.M > MassB.N) Then

Begin

IF VS_IfMassEq(MAssA, MAssB)

Then

BEgin

VS_VerMass(MAssA, MAssB);

VS_InitMassPErebor;

VS_Init2xMassPerebot ;

VS_SortMassPerebor;

VS_GetMAssForDet;

ResultMemo.Lines.Add('Итого по формуле Коши - Бине: ' + FloattoStr(VS_GetKoshi_Bine))

end{IF VS_IfMassEq(MAssA, MAssB)}

Else ResultMemo.Lines.Add('Матрицы не равны')

end;{If (MassA.M < MassA.N) And (MassB.M > MassB.N) Then}

end;

procedure TMainForm.DetCClick(Sender: TObject);

Var Det : Real;

begin

Det := VS_Det(MassC); //ВЫчисляем определитель

ResultMemo.Lines.Add('Определитель матрицы C равен ' + FloattoStr(Det)); //Выводим результат в Мемо

ShowMessage(FloatToStr(Det)); //Выводим результат в диалоговое окно

end;

function TMainForm.VS_Minor(II, Jj: Integer; InMass : TVS_MassData): REal;

//Вычислаем минор

Var

Col, //Текущий столбец новой матрицы

Row, //Текущая строка новой матрицы

I, J : Integer;

TempMass : TVS_MassData;

begin

If InMass.M <> InMass.N Then Exit; // Матрица не квадратная - убегаем

SetLength(TempMass.Mass, InMass.M -1, InMass.N -1);//Установили размер матрицы

Row := 0;

For I := 0 To InMass.M -1 Do

begin

Col := 0; //Начали новый массив с первого элемента

If I <> II -1 Then

Begin //Отбрасываем I строку

For J := 0 To InMass.N -1 do

If J <> JJ -1 Then

Begin //Перебираем все столюцы, кроме J

TempMass.Mass[Row,Col] := InMass.Mass[I,J];

Inc(Col);

end;{If J <> JJ Then}

Inc(Row); //Перешли на сл. строку для нового массива

end;{If I <> II Then}

end; {For I := 0 To InMass.M Do}

TempMass.M := InMass.M - 1;

TempMass.N := InMass.N - 1;

Result := VS_Det(TempMass);

end;

procedure TMainForm.AssignMass(InMAss: TVS_MassData;

var OutMass: TVS_MassData);

//Передаем данные из InMass в OutMass;

Var

I,

J : Integer;

begin

for i := 0 to InMAss.M - 1 do //Пробегаемся по строкам

for j := 0 to InMAss.N - 1 do //Пробегаемся по столбцам

OutMass.Mass[i, j] := InMass.Mass[i, j]; //Переносим значения из InMAss в OutMas

OutMass.M := InMAss.M; //Переносим число, определяющее количество строк

OutMass.N := InMAss.N; //Переносим число, определяющее количество столбцов

OutMass.Name := InMAss.Name; //Переносим название массива

end;

procedure TMainForm.VS_MinorMass(InMass : TVS_MassData; var OutMass: TVS_MassData);

//Находим все миноры входящей матрицы

//InMass - массив, в котором будем искать миноры

//OutMass - массив минор

Var

i,

j : Integer;

begin

If InMass.M <> InMass.N Then Exit; //Вышли, так как мартица не квадратная

For I := 0 to InMass.M - 1 Do //пробегаемся по строкам

For J := 0 To InMass.N - 1 do //Пробегаемся по столбцам

OutMass.Mass[I,J] := VS_Minor(I +1, J +1 , InMass); //Получили I, J минор и занесли в массив OutMass

OutMass.M := InMass.M;

OutMass.N := InMass.N;

end;

procedure TMainForm.N6Click(Sender: TObject);

begin

VS_MinorMass(MassA, MassC);

VS_ShowMass('Минор', MassC);

VS_ShowMassToMemo('Минор', MassC);

end;

procedure TMainForm.N7Click(Sender: TObject);

begin

VS_MinorMass(MassB, MassC);

VS_ShowMass('Минор', MassC);

VS_ShowMassToMemo('Минор', MassC);

end;

procedure TMainForm.N8Click(Sender: TObject);

begin

VS_MinorMass(MassC, MassC);

VS_ShowMass('Минор', MassC);

VS_ShowMassToMemo('Минор', MassC);

end;

procedure TMainForm.lll1Click(Sender: TObject);

begin

IF VS_IfMassEq(MAssA, MAssB)

Then

BEgin

VS_VerMass(MAssA, MAssB);

VS_InitMassPErebor;

VS_Init2xMassPerebot ;

VS_SortMassPerebor;

VS_GetMAssForDet;

ResultMemo.Lines.Add('Итого по форуме Коши - Бине: ' + FloattoStr(VS_GetKoshi_Bine))

end

Else ResultMemo.Lines.Add('Матрицы не равны')

end;

procedure TMainForm.VS_InitMassPErebor;

//Создаем массив переборов для вычесления Детерминант формулы Коши-Бине

// Все действия делаются над массивом MAssP

Var

I, J, Curr : Integer;

begin

Curr := 0; //Текущий элемент массива

SetLength(MassP, MassA.N * MassA.M); //Установили размерность

For I := 0 to MassA.M -1 do //Пробегаемся по строкам

For J := 0 to MassA.N -1 do //Пробегаемся по столбцам

Begin

MassP[Curr] := J +1; //Заполняем массив строками-перестановками/столбцами-перестановками

Inc(Curr); //Перешли к след. элеенту массива

end;

//VS_SortMassPerebor

end;

procedure TMainForm.VS_GetMAssForDet;

//Формуриуем массив для вычисления Дет.

//Данные перестановки уже должны хранится в массиве MassP

//т. е уже нужно иметь Массив А и уже должна быть выполнена VS_InitMassPErebor;

Var I, J : Integer;

Det : Real;

SA, SB : String;

TempB,

TempA : TVS_MassData; //Н*М мерный массив миноров

begin

ResultMemo.Lines.Add('Переборы: ');

SetLength(TempA.Mass, MAssA.M, MAssA.M);

SetLength(TempB.Mass, MAssB.N, MAssB.N);

SetLength(DetA, MassA.N);

SetLength(DetB, MassB.M);

TEmpA.M := MAssA.M;

TEmpA.N := MAssA.M;

TEmpB.M := MAssB.N;

TEmpB.N := MAssB.N;

For I := 0 to MassPer.M - 1 do //пробегаемся по строкам

Begin

SA:= IntToStr(I +1) + 'A) ';

SB:= IntToStr(I +1) + 'B) ';

For J := 0 to MassPer.N - 1 do //Пробегаемся по всем столбцам -1

begin

SA:= SA + FloatToStr(MassPer.Mass[I, J]) + ' ';

SB:= SB + FloatToStr(MassPer.Mass[I, J]) + ' ';

VS_GenerateColMinorData(J, Trunc(MassPer.Mass[I, J]), TempA);

VS_GenerateRowMinorData(J, Trunc(MassPer.Mass[I, J]), TempB);

end;{For J := 0 to MassPer.N - 1 do //Пробегаемся по всем столбцам -1}

ResultMemo.Lines.Add('');

ResultMemo.Lines.Add(SA);

VS_ShowMassToMemo('', TempA, False);

DetA[I] := VS_Det(TempA);

ResultMemo.Lines.Add('DetA = ' + FloatToStr(Deta[I]));

ResultMemo.Lines.Add('');

ResultMemo.Lines.Add(SB);

VS_ShowMassToMemo('', TempB, False);

DetB[I] := VS_Det(TempB);

ResultMemo.Lines.Add('DetB = ' + FloatToStr(DetB[I]));

end;{For I := 0 to MassPer.M - 1 do //пробегаемся по строкам}

end;

procedure TMainForm.VS_GenerateColMinorData(CurCol, Col: Integer;

var inMass: TVS_MassData);

//Формируем массив минор для КоШИ_БИНЕ

//На входе

//CurCol - номер столбюца в новом массиве

//COl - номер столбца для массива, с которого будем брать значения

//InMass - массив, в который будем заносить значения

Var I : Integer;

begin

For I := 0 To MassA.M -1 do

inMass.Mass[I, CurCol] := MassA.Mass[I, Col -1];

end;

procedure TMainForm.VS_SortMassPerebor;

//Сортируем элементы массива переборов для правильного вычисления миноров

Var

K, I, J, Curr : Integer;

Rez : Real;

begin

For I := 0 to MassPer.M - 1 do //пробегаемся по строкам

For J := 0 to MassPer.N - 2 do //Пробегаемся по всем столбцам -1

For K := J + 1 to MassPer.N - 1 do

If MassPer.Mass[I, j] > MassPer.Mass[I, K] Then //Текущий элемент больше следующего - меняем местами

Begin

REz := MassPer.Mass[I, j];

MassPer.Mass[I, j] := MassPer.Mass[I, K];

MassPer.Mass[I, K] := Rez;

end;

end;

procedure TMainForm.VS_Init2xMassPerebot;

//Формируем 2хмерный массив переборов

//На выходе будет M*N мерный массив переборов (не сортированый)

Var I, J, Curr, CurCol, CurRow : Integer;

Det : Real;

S : String;

begin

Curr := 0; //Текущий элемент в массиве MassP

SetLEngth(MassPer.Mass, MassA.N, MassA.M); //Установвили размерность массива перестановок

MassPer.M := MassA.N; //Задали размерность

MassPer.N := MassA.M; //Задали размерность

CurRow := 0; //Текущая строка нового массива

For I := 0 to MassA.N -1 Do //Запускаем по строкам

begin

CurCol := 0; // Текущий столбец/строка нового массива

For J := 0 to MassA.M - 1 do

Begin

MassPer.Mass[CurRow, CurCol] := MassP[Curr];

Inc(Curr); //Перешли к новому элементу массива MassP

Inc(CurCol); //Перешли к нововму столбцу нового массива

end; {For J := 0 to MassA.M - 1 do}

Inc(CurRow); //Перешли к новой строке нового массива

end;{For I := 0 to MassA.N -1 Do //Запускаем}

end;

procedure TMainForm.VS_GenerateRowMinorData(CurCol, Col: Integer;

var InMass: TVS_MassData);

//Формируем массив минор для КоШИ_БИНЕ

//На входе

//CurCol - номер столбюца в новом массиве

//COl - номер столбца для массива, с которого будем брать значения

//InMass - массив, в который будем заносить значения

Var I : Integer;

begin

For I := 0 To MassB.N -1 do

inMass.Mass[CurCol, I ] := MassB.Mass[Col -1,I];

end;

Function TMainForm.VS_GetKoshi_Bine: Real;

//Вычисляем формулу Коши-Бине

// ьПеред вызовом должны быть выполнены след. условия:

//1 - введен масив а и б

//выполнены след. процедуры

//VS_InitMassPErebor;

//VS_Init2xMassPerebot ;

//VS_SortMassPerebor;

//VS_GetMAssForDet

//

Var I : Integer;

S : String;

begin

Result := 0;

S := '';

For I := 0 to MassA.N - 1 do

Begin

REsult := REsult + DetA[I] * Detb[I];

S := S + ' (' + FloattoStr(DetA[I])+ ')*(' + FloattoStr(DetB[I] ) + ') + ';

end;

ResultMemo.Lines.Add('C = ' + (Copy(S, 1, Length(s) -2)));

end;

function TMainForm.VS_IfMassEq(Massin1, MAssIn2: TVS_MassData): Boolean;

//Сравниваем 2 мартицы

//Получаем True, если

//1. число строк матрицы 1 - числу столбцов матрицы 2

//2. число стоблцов матрицы 1 = числу строк матрицы 2

begin

Result := (Massin1.M = MAssIn2.N) And (Massin1.N = MAssIn2.M)

end;

procedure TMainForm.VS_VerMass(var Massin1, MAssIn2: TVS_MassData);

//Проверяем матрицы

//Если Столбцв матрицы А меньше, чем в Б, меняем матрицы местами

Var TempMass: TVS_MassData;

begin

If Massin1.N < MAssIn2.N Then

Begin

SetLength(TempMass.Mass, MassIn1.M, MassIn1.N);

TempMass := Massin1;

SetLength(Massin1.Mass, MassIn2.M, MassIn2.N);

Massin1 := MAssIn2;

SetLength(Massin2.Mass, TempMass.M, TempMass.N);

MAssIn2 := TempMass;

end;

end;

procedure TMainForm.VS_LoadData(var InMAss: TVS_MassData);

//Загружаем данные из файла в Массив InMAss

Var F : TextFile; //Описали переменную работы с текстовым файлом

RezStr : String;

CurRow,

MaxCol,

MaxRow,

CorCol : Integer;

begin

OpenDialog.DefaultExt := '*.txt'; //Расширение файлов по умочлчанию

OpenDialog.InitialDir := ExtractFilePath(Application.ExeName); //Открываем каталог, в котором запущена наша программа

MaXcol := 0;

;

If OpenDialog.Execute Then

Begin //Если пользователь нажал на ОК и выбрал файл - начинаем загрузку

AssignFile(F, OpenDialog.FileName);

If FileExists(OpenDialog.FileName) Then

Reset(f) //Файл есть, открываем

Else Exit; //Файла нету, выходим

CurRow := 0;

VS_GetRazmOnFile(OpenDialog.FileName, MaxCol, MaxRow);

SetLEngth(InMAss.Mass, MaxRow, MaxCol);

While Not Eof(F) Do

Begin

REadLn(F, RezStr);

VS_InitMassInStr(RezStr, CurRow, InMAss);

// ResultMemo.Lines.Add(RezStr);

Inc(CurRow);

end;{While Not Eof(F) Do}

InMass.M := MaxRow;

InMAss.N := MaxCol;

VS_ShowMassToMemo('Успешно загружен', InMAss);

end;{If OpenDialog.Execute Then}

end;

procedure TMainForm.N9Click(Sender: TObject);

begin

VS_LoadData(MassA);

end;

procedure TMainForm.VS_InitMassInStr(InStr: String; CurRow: Integer;

var InMass: TVS_MassData);

//Формируем строку элементов массива.

Var

N : Integer;

RezStr : String;

CurCol : Integer;

begin

inStr := Trim(InStr); //Удалили пробелы с обоих концов строки

CurCol := 0;

While Length(InStr) > 0 Do

Begin //Запускаем цикл до тех пор, пока строка имеет значения

N := Pos(#32, InStr); //Нашли ближайший пробел

If N <> 0 Then

Begin // Действительно у нас нашелся прьблел

RezStr := Copy(inStr, 1, N);

Delete (inStr,1, N);

RezStr := Trim(RezStr); //Удалили лишние пробелы

Try //Включаем обработку ошибок

InMass.Mass[CurRow, CurCol] := StrtoFloat(RezStr); //Присваиваем элемент массива из строк

except //Если авария

InMass.Mass[CurRow, CurCol] := 0; //Присваиваем элемнту 0

end;

Inc(CurCol);//Перешли к след. стобцу массива

end {If N <> 0 Then}

Else

//Пробела нету, возможно, это последний символ

If Length(InStr)> 0 Then

Begin //Есть значение

Try //Включаем обработку ошибок

InMass.Mass[CurRow, CurCol] := StrtoFloat(InStr); //Присваиваем элемент массива из строк

except //Если авария

InMass.Mass[CurRow, CurCol] := 0; //Присваиваем элемнту 0

end;

Inc(CurCol);//Перешли к след. стобцу массива

InStr := '';

end; {If Length(InStr)> 0 Then}

end;

end;

procedure TMainForm.VS_GetRazmOnFile(FileName: String; var Col,

Row: Integer);

Var F : TextFile; //Описали переменную работы с текстовым файлом

RezStr : String;

begin

Col := 0;

Row := 0;

AssignFile(F, FileName);

Reset(F);

While Not Eof(F) Do

Begin

ReadLn(F, RezStr);

If (Row = 0) And (Length(RezStr)<> 0) Then Col := VS_GetColOnFile(RezStr);

Inc(Row);

end;{While Not Eof(F) Do}

CloseFile(f);

end;

function TMainForm.VS_GetColOnFile(InStr: String): Integer;

Var

N : Integer;

RezStr : String;

begin

inStr := Trim(InStr); //Удалили пробелы с обоих концов строки

Result := 0;

While Length(InStr) > 0 Do

Begin //Запускаем цикл до тех пор, пока строка имеет значения

N := Pos(#32, InStr); //Нашли ближайший пробел

If N <> 0 Then

Begin // Действительно у нас нашелся прьблел

RezStr := Copy(inStr, 1, N);

Delete (inStr,1, N);

RezStr := Trim(RezStr); //Удалили лишние пробелы

Inc(Result);//Перешли к след. стобцу массива

end {If N <> 0 Then}

Else

//Пробела нету, возможно, это последний символ

If Length(InStr)> 0 Then

Begin //Есть значение

Inc(Result);//Перешли к след. стобцу массива

InStr := '';

end; {If Length(InStr)> 0 Then}

end;

end;

procedure TMainForm.N10Click(Sender: TObject);

begin

VS_LoadData(MassB);

end;