Навигация
Критерий наиболее вероятного исхода
4. Критерий наиболее вероятного исхода.
Этот критерий предполагает замену случайной ситуации детерминированной путем замены случайной величины прибыли (или затрат) единственным значением, имеющим наибольшую вероятность реализации. Использование данного критерия, также как и в предыдущем случае в значительной степени опирается на опыт и интуицию. При этом необходимо учитывать два обстоятельства, затрудняющие применение этого критерия:
· критерий нельзя использовать, если наибольшая вероятность события недопустимо мала;
применение критерия невозможно, если несколько значений вероятностей возможного исхода равны между собой.5. Учет неопределенных факторов, заданных законом распределения.
Случай, когда неопределенные факторы заданы распределением, соответствует ситуации риска. Этот случай может учитываться двумя путями. Первый - анализом адаптивных возможностей, позволяющих реагировать на конкретные исходы; второй - методически, при сопоставлении эффективности технических решений. Суть первого подхода заключается в том, что законы распределения отдельных параметров на этапе проектирования могут быть определены с достаточной степенью приближения на основе сопоставления с аналогами, из физических соображений или на базе статистических данных и данных прогнозов.
Методический учет случайных факторов, заданных распределением, может быть выполнен двумя приемами: заменой случайных параметров их математическими ожиданиями (сведением стохастической задачи к детерминированной) и "взвешиванием" показателя качества по вероятности (этот прием иногда называют "оптимизация в среднем").
Первый прием предусматривает определение математического ожидания случайной величины v - M(v) и определение зависимости W(M(v)), которая в дальнейшем оптимизируется по u. Однако сведение к детерминированной схеме может быть осуществлено в тех случаях, когда диапазон изменения параметра u невелик или когда зависимость W(u) линейна или близка к ней.
Второй прием предусматривает определение W в соответствии с зависимостями соответственно для дискретных и непрерывных величин:
![]() ; (1.6)
; (1.6)
![]() , (1.7)
, (1.7)
где
P(ui) - ряд распределений случайной величины ui;
f(ui) - плотность распределения случайной величины u.
При описании дискретных случайных величин наиболее часто используют распределения Пуассона, биноминальное. Для непрерывных величин основными распределениями являются нормальное, равномерное и экспоненциальное.
1.2.1. Постановка задачи стохастического программирования
При перспективном и оперативном планировании работы лесопромышленного предприятия возникает необходимость в учете ряда случайных факторов, существенно влияющих на процесс производства. К таким факторам относятся спрос, который не всегда может быть предсказуем, непредусмотренные сбои в поступлении сырья, энергии, рабочей силы, неисправности и аварии оборудования. Еще больше случайных факторов необходимо учитывать при планировании лесохозяйственного производства, эффективность которого зависит от климатических условий, урожайности и т.д. Поэтому задачи планирования лесного производства целесообразно ставить и исследовать в терминах и понятиях стохастического программирования, когда элементы задачи линейного программирования (матрица коэффициентов A, вектора ресурсов b, вектора оценок c) часто оказываются случайными. Подобного типа задачи ЛП принято классифицировать как задачи стохастического программирования (СП).
Подходы к постановке и анализу стохастических задач существенно различаются в зависимости от последовательности получения информации - в один прием или по частям. При построении стохастической модели важно также знать, необходимо ли принять единственное решение, не подлежащее корректировке, или можно по мере накопления информации один или несколько раз корректировать решение. В соответствии с этим в стохастическом программировании исследуются одноэтапные, двухэтапные и многоэтапные задачи.
В одноэтапных задачах решение принимается один раз и не корректируется. Они различаются по показателям качества решения (по целевым функциям), по характеру ограничений и по виду решения.
Задача СП может быть сформулирована в M- и P- постановках по отношению к записи целевой функции и ограничений.
Случайны элементы вектора с (целевая функция).
При M-постановке целевая функция W записывается в виде
![]() , (1.8)
, (1.8)
что означает оптимизацию математического ожидания целевой функции. От математического ожидания целевой функции можно перейти к математическому ожиданию случайной величины cj
![]() . (1.9)
. (1.9)
При P- постановке имеем:
· при максимизации
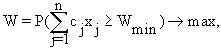 (1.10)
(1.10)
где
Wmin - предварительно заданное допустимое наихудшее (минимальное) значение целевой функции.
· при минимизации
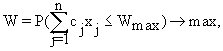 (1.11)
(1.11)
где
Wmax - предварительно заданное допустимое наихудшее (максимальное) значение целевой функции.
Суть P-постановки заключается в том, что необходимо найти такие значения xj, при которых максимизируется вероятность того, что целевая функция будет не хуже предельно допустимого значения.
Ограничения задачи, которые должны выполняться при всех реализациях параметров условий задачи, называются жесткими ограничениями. Часто возникают ситуации, в которых постановка задачи позволяет заменить жесткие ограничения их усреднением по распределению случайных параметров. Такие ограничения называют статистическими:
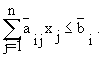 (1.12)
(1.12)
В тех случаях, когда по содержательным соображениям можно допустить, чтобы невязки в условиях не превышали заданных с вероятностями, небольшими i>0, говорят о стохастических задачах с вероятностными ограничениями:
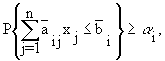 (1.13)
(1.13)
т.е. вероятность выполнения каждого заданного ограничения должна быть не менее назначенной величины i. Параметры i предполагаются заданными или являются решениями задачи более высокого уровня.
Представленные задачи как в M-, так и в P- постановках непосредственно решены быть не могут. Возможным методом решения этих задач является переход к их детерминированным эквивалентам. В основе этого перехода лежит использование закона распределения случайной величины. В инженерной практике наиболее часто используется нормальный закон распределения, поэтому дальнейшие зависимости приведем для этого случая.
Принимаем, что aij, bi, cj подчинены нормальному закону распределения. В этом случае будет справедлива следующие детерминированные постановки:
· P - постановка целевой функции, максимизация:
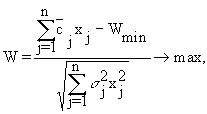 (1.14)
(1.14)
где
![]() и j - математическое ожидание и среднее квадратическое отклонение случайной величины cj.
и j - математическое ожидание и среднее квадратическое отклонение случайной величины cj.
· P - постановка целевой функции, минимизация:
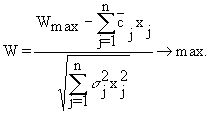 (1.15)
(1.15)
· Вероятностные ограничения:

где
![]() - соответственно, математические ожидания и дисперсии случайных величин aij и bi;
- соответственно, математические ожидания и дисперсии случайных величин aij и bi;
![]() - значение центрированной нормированной случайной величины в нормальном законе распределения, соответствующей заданному уровню вероятности соблюдения ограничений i.
- значение центрированной нормированной случайной величины в нормальном законе распределения, соответствующей заданному уровню вероятности соблюдения ограничений i.
Сделаем несколько замечаний к приведенным зависимостям:
· задача стохастического программирования сведена к задаче нелинейной оптимизации и может быть решена одним из рассматриваемых ранее методов;
сравнение ограничения ресурса в стохастическом программировании и аналогичным ограничением в задаче линейного программирования показывает, что учет случайного характера величин aij и bi приводит к уменьшению располагаемого ресурса на величину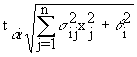 , (1.16)
, (1.16)
т.е. к необходимости в дополнительном ресурсе. Однако этот дополнительный ресурс может оказаться неиспользованным, но для гарантированного выполнения плана его иметь необходимо.
Применение стохастического программирования в лесном делеПример 1.1. Распределение посевной площади между лесными культурами.
Лесничество имеет вырубки площадью в 100 га в различных почвенных условиях (три типа) и заинтересовано как можно более эффективно использовать ее для создания лесных культур. Требуется распределить площадь под посевы лесных культур - сосны и ели. Имеются статистические данные по издержкам и всхожести каждой культуры на единице площади с почвой каждого типа. Кроме того, вышестоящей организацией задан минимально необходимый объем лесовосстановления по каждой культуре - 30 для сосны и 40 для ели. Издержки на обработку почвы и всхожесть лесных культур существенно зависят от погодных условий и являются случайными величинами с параметрами риска:
· 0, характеризующий риск превышения фактических издержек над запланированными;
1 и 1, определяющие риск невыполнения плана по культуре i.Постановка задачи.
1. В качестве показателя эффективности целесообразно взять издержки лесовосстановления.
2. В качестве управляемых переменных задачи следует взять:
x11 - площадь с 1 типом почвы, отводимой под культуру сосны;
x12 - площадь с 1 типом почвы, отводимой под культуру ели;
x21 - площадь с 2 типом почвы, отводимой под культуру сосны;
x22 - площадь с 2 типом почвы, отводимой под культуру ели;
x31 - площадь с 3 типом почвы, отводимой под культуру сосны;
x32 - площадь с 3 типом почвы, отводимой под культуру ели.
3. Целевая функция:
c11 x11 + c11 x12 + c11 x13 + c11 x21 + c11 x22 + c11 x23 + c11 x31 + c11 x32 + c11 x33 min,
где
c11 - удельные затраты площади с почвой типа 1 для посадки сосны;
c12 - удельные затраты площади с почвой типа 1 для посадки ели;
c21 - удельные затраты площади с почвой типа 2 для посадки сосны;
c22 - удельные затраты площади с почвой типа 2 для посадки ели;
c31 - удельные затраты площади с почвой типа 3 для посадки сосны;
c32 - удельные затраты площади с почвой типа 3 для посадки ели.
4. Ограничения:
4.1. По использованию земли, га:

4.2. По бюджету, тыс. руб.:
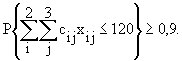
4.3. По обязательствам, га:
для сосны
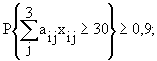
для ели
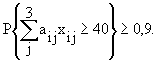
4.4. Областные ограничения:
x11 0,..., x33 0.
Пример 1.2. Выбор состава машинно-тракторного парка.
Выбор структуры технического оснащения является необходимым элементом лесохозяйственного планирования. Машины различных марок, предназначенные для одних и тех же работ, обладают разными конструктивными параметрами и характеризуются неодинаковой эффективностью. Для каждого конкретного хозяйства требуется подобрать состав машинно-тракторного парка, наиболее полно отвечающий его особенностям. Рациональный подбор техники должен минимизировать приведенные затраты на производство заданных работ в требуемые сроки. Объемы работ, производительность агрегатов и приведенные затраты зависят от сложившихся погодных условий и множества других непредсказуемых факторов. Поэтому выбор структуры машинно-тракторного парка следует связать с решением стохастической задачи.
Постановка задачи.
1. В качестве показателя эффективности целесообразно взять суммарные приведенные издержки на приобретение, обслуживание и эксплуатацию техники.
2. В качестве управляемых переменных задачи следует взять:
x1 - количество плугов - покровасдирателей;
x2 - количество плугов лесных;
x3 - количество плугов лесных ПЛ;
x4 - количество тракторов ЛХТ-55А;
x5 - количество тракторов ТДТ-55А;
x6 - количество тракторов МТЗ.
3. Целевая функция:
c1 x1 + c2 x2 + c3 x3 + c4 x4 + c5 x5 + c6 x6 min,
где
c1 - приведенные затраты на плуг - покровасдиратель;
c2 - приведенные затраты на плуг лесной;
c3- приведенные затраты на плуг лесной;
c4 - приведенные затраты на трактор ЛХТ-55А;
c5 - приведенные затраты на трактор ТДТ-55А;
c6 - приведенные затраты на трактор МТЗ.
4. Ограничения:
4.1. По условию обеспечения необходимой комплексной работы агрегатов:
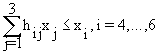 ,
,
где
hij = 1, если плуг j типа работает с трактором i типа;
hij = 0, в противном случае.
4.2. По обязательствам выполнения требуемых работ, га:
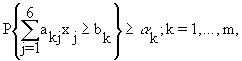
где
akj, k = 1,2,...,m, j = 1,..., 3 - производительность плуга j типа на работе k типа;
bk , - объем работ k вида, подлежащих выполнению.
4.3. Областные ограничения:
x1 0,..., x6 0.
1.2.3. Метод статистического моделирования
Приведенные формулы (1.6) и (1.7) могут быть использованы для систем независимых случайных величин. Однако для технических систем, как правило, случайные параметры являются зависимыми. Причем эта зависимость не функциональная, а корреляционная. Поэтому для анализа случайных факторов, заданных распределением, широкое применение нашли теория марковских процессов и метод статистического моделирования (метод Монте-Карло).
В задачах принятия оптимальных решений широкое применение получил метод Монте-Карло. Основными особенностями этого метода, основанного на многократном повторении одного и того же алгоритма для каждой случайной реализации, являются: универсальность (метод не накладывает практически никаких ограничений на исследуемые параметры, на вид законов распределения); простота расчетного алгоритма; необходимость большого числа реализаций для достижения хорошей точности; возможность реализации на его основе процедуры поиска оптимальных параметров проектирования. Отметим основные факторы, определившие применение метода статистического моделирования в задачах исследования качества при проектировании: метод применим для задач, формализация которых другими методами затруднена или даже невозможна; возможно применение этого метода для машинного эксперимента над не созданной в натуре системы, когда натурный эксперимент затруднен, требует больших затрат времени и средств или вообще не допустим по другим соображениям.
Похожие работы
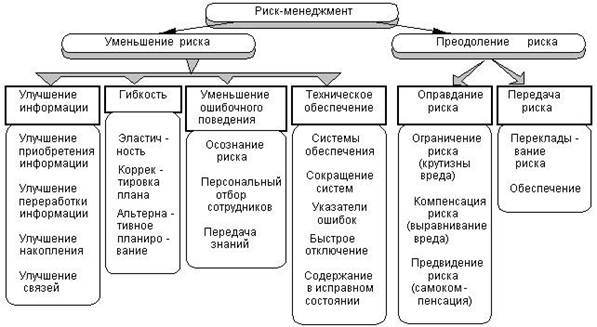
... сумм расходов, продажи, кредита; § самострахование за счет создания натуральных и денежных резервных (страховых) фондов; § страхование. Таким образом, в процессе разработки и принятия управленческих решений в условиях неопределенности и риска менеджер сталкивается с необходимостью проведения анализа существующих рисков, а также осуществления мероприятий, связанных с избежанием, удержанием, ...
... сумм расходов,продажи, кредита; · самострахование за счет создания натуральных и денежных резервных (страховых) фондов; · страхование. Таким образом, в процессе разработки и принятия управленческих решений в условиях неопределенности и риска менеджер сталкивается с необходимостью проведения анализа существующих рисков, а также осуществления мероприятий, связанных с избежанием, удержанием, ...
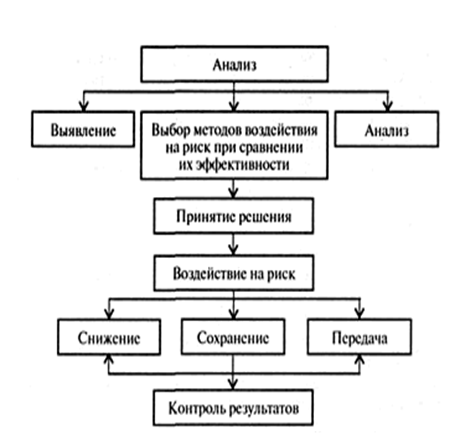
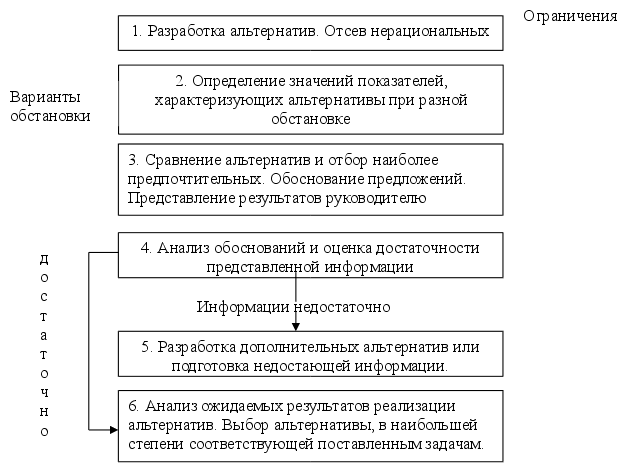
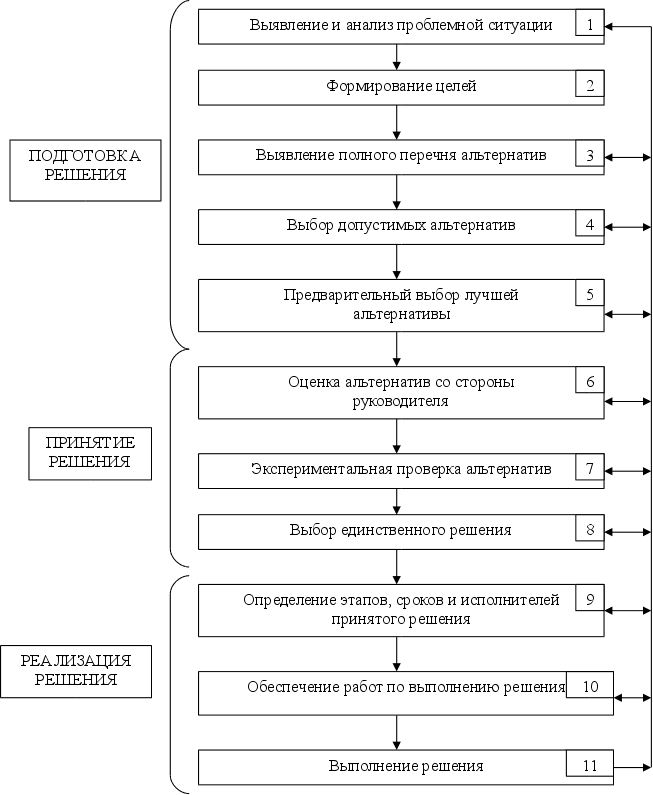
... вопросы в свою очередь связаны с принятием определенных решений, однако в настоящее время они в значительной мере определяются вкусом, склонностями и личными качествами.1.2.2. Сущность процесса принятия управленческого решения Понятие "решение" в научной литературе трактуется по-разному. Оно понимается и как процесс, и как акт выбора, и как результат выбора. Решение как процесс характеризуется ...
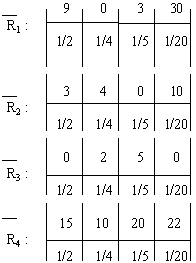
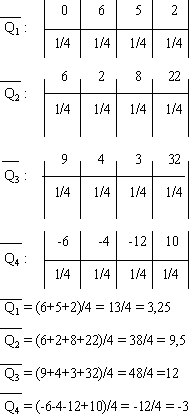
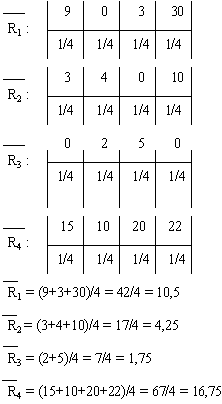
... = -1 Итак, мы имеем i1 = 3, i2 = 12, i3 = 17.5, i4 = -1. Теперь из чисел 3, 12, 17.5, -1 берем максимальное. Это — 17.5. Значит, правило Гурвица рекомендует 3-е решение. Принятие решений в условиях частичной неопределенности. Предположим, что в рассматриваемой схеме известны вероятности pj того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной ...
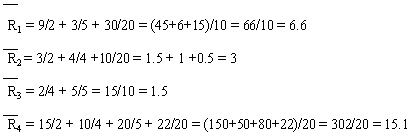
0 комментариев