Сидоренков В.В., МГТУ им. Н.Э. Баумана
Показано, что электромагнитный векторный потенциал как физическая величина представляют собой полевой эквивалент локальных характеристик микрочастицы: ее электрическому заряду, кратному кванту электрического потока - заряду электрона, соответствует электрическая компонента векторного потенциала, а удельному (на единицу заряда) кинетическому моменту, кратному кванту магнитного потока, отвечает магнитная компонента векторного потенциала.
Полевая концепция природы электричества является фундаментальной основой классической электродинамики [1] и базируется на признании того факта, что взаимодействие разнесенных в пространстве электрических зарядов осуществляется посредством электромагнитных полей. Свойства этих полей описываются системой электродинамических уравнений Максвелла, откуда непосредственно следуют и понятия электрического и магнитного векторных потенциалов, физический смысл которых, несмотря на вполне определенный прогресс в установлении их физической значимости в приложениях квантовой механики [2, 3] и электродинамики [4, 5], по сей день остается по существу так и не выясненным.
Попытаемся разобраться в этом вопросе, для чего воспользуемся системой указанных уравнений электромагнитного поля [1]:
(a) ![]() , (b)
, (b) ![]() ,
,
(c) 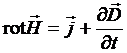 , (d)
, (d) ![]() . (1)
. (1)
включающей в себя так называемые материальные соотношения:
![]() ,
, ![]() ,
, ![]() ,
,
описывающие отклик среды на наличие в ней электромагнитных полей. Здесь ![]() и
и ![]() векторы напряженности электрического и магнитного полей, связанные с соответствующими векторами индукции
векторы напряженности электрического и магнитного полей, связанные с соответствующими векторами индукции ![]() и
и ![]() ,
, ![]() вектор плотности электрического тока,
вектор плотности электрического тока, ![]() объемная плотность стороннего заряда,
объемная плотность стороннего заряда, ![]() и
и ![]() электрическая и магнитная постоянные,
электрическая и магнитная постоянные, ![]() ,
, ![]() и
и ![]() удельная электрическая проводимость и относительные диэлектрическая и магнитная проницаемость среды, соответственно.
удельная электрическая проводимость и относительные диэлектрическая и магнитная проницаемость среды, соответственно.
Представления о векторных потенциалах возникают как следствие того, что дивергенция ротора любого вектора тождественно равна нулю. Поэтому магнитную компоненту векторного потенциала ![]() можно ввести посредством дивергентного соотношения
можно ввести посредством дивергентного соотношения ![]() системы уравнений (1), а электрическую компоненту
системы уравнений (1), а электрическую компоненту ![]() соотношением
соотношением ![]() , описывающим поляризацию локально электронейтральной среды:
, описывающим поляризацию локально электронейтральной среды:
а) ![]() , (b)
, (b) ![]() . (2)
. (2)
Однозначность функций векторных потенциалов, то есть чисто вихревой характер таких полей, обеспечивается условием калибровки: ![]() . Видно, что с физической точки зрения рассматриваемые потенциалы являются поляризационными потенциалами.
. Видно, что с физической точки зрения рассматриваемые потенциалы являются поляризационными потенциалами.
Тогда подстановка соотношения (2a) в уравнение вихря электрической напряженности (1а) приводит к известной формуле [1, 2] связи поля вектора указанной напряженности с магнитным векторным потенциалом:
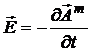 , (3)
, (3)
описывающей закон электромагнитной индукции Фарадея. Электрический скалярный потенциал: ![]() здесь не рассматривается, как не имеющий отношения к обсуждаемым в работе вихревым полям.
здесь не рассматривается, как не имеющий отношения к обсуждаемым в работе вихревым полям.
При аналогичной подстановке соотношения (2b) в уравнение вихря магнитной напряженности (1c) с учетом закона Ома процесса электропроводности ![]() получаем в итоге связь этой напряженности с электрическим векторным потенциалом:
получаем в итоге связь этой напряженности с электрическим векторным потенциалом:
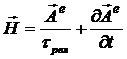 , (4)
, (4)
где ![]() постоянная времени релаксации электрического заряда в среде за счет электропроводности. Таким образом, согласно соотношениям (3) и (4), векторные потенциалы – это не математические фикции, а физически значимые фундаментальные поля, порождающие традиционные вихревые электромагнитные поля. Подробное обсуждение физической значимости векторных потенциалов в классической электродинамике представлено в работах [4, 5].
постоянная времени релаксации электрического заряда в среде за счет электропроводности. Таким образом, согласно соотношениям (3) и (4), векторные потенциалы – это не математические фикции, а физически значимые фундаментальные поля, порождающие традиционные вихревые электромагнитные поля. Подробное обсуждение физической значимости векторных потенциалов в классической электродинамике представлено в работах [4, 5].
Поскольку взаимодействие электрических зарядов реализуются посредством электрических и магнитных полей, то физически нетривиально предположить, что порождающие эти поля векторные потенциалы как физические величины есть первичные полевые характеристики самого заряда, его полевой эквивалент. Для обоснования правомерности такого предположения рассмотрим конкретные аргументы, позволяющие, наконец, разрешить проблему физического смысла электромагнитных векторных потенциалов, которую для магнитной компоненты векторного потенциала обсуждал еще Максвелл при анализе своих электродинамических уравнений ([6] п. 590).
Как известно, физические представления об электрическом заряде имеют на микроуровне существенное дополнение: элементарная частица характеризуется не только значением заряда ![]() , кратного заряду электрона
, кратного заряду электрона ![]() , но и спином
, но и спином ![]() , трактуемым как собственный момент количества движения (кинетический момент) частицы. Величина этого момента квантована значением
, трактуемым как собственный момент количества движения (кинетический момент) частицы. Величина этого момента квантована значением ![]() , где h постоянная Планка. Согласно нашему предположению, сопоставим эти локальные характеристики микрочастицы и ее некое собственное первичное электромагнитное поле. Так, например, для электрона электрическая компонента этого поля соответствует кванту электрического потока заряду e, а магнитная компонента – величине его удельного (на единицу заряда) кинетического момента
, где h постоянная Планка. Согласно нашему предположению, сопоставим эти локальные характеристики микрочастицы и ее некое собственное первичное электромагнитное поле. Так, например, для электрона электрическая компонента этого поля соответствует кванту электрического потока заряду e, а магнитная компонента – величине его удельного (на единицу заряда) кинетического момента ![]() , определяющей, как известно (например, [2]), квант магнитного потока. Наша задача показать далее, что введенное здесь гипотетическое собственное поле микрочастицы (совокупно, и макрообъекта) является именно полем электромагнитных векторных потенциалов.
, определяющей, как известно (например, [2]), квант магнитного потока. Наша задача показать далее, что введенное здесь гипотетическое собственное поле микрочастицы (совокупно, и макрообъекта) является именно полем электромагнитных векторных потенциалов.
Вначале рассмотрим электрический векторный потенциал ![]() . Для этого соотношение (2b) связи вектора электрической индукции и вектор-потенциала для большей наглядности и математической общности представим в интегральной форме:
. Для этого соотношение (2b) связи вектора электрической индукции и вектор-потенциала для большей наглядности и математической общности представим в интегральной форме:
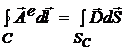 =
= 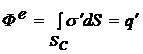 . (5)
. (5)
Эти интегральные соотношения устанавливают физически содержательное положение о том, что величина циркуляции вектора ![]() по замкнутому контуру С определяется электрическим потоком
по замкнутому контуру С определяется электрическим потоком ![]() через поверхность
через поверхность ![]() , опирающейся на этот контур, следовательно, поляризационным электрическим зарядом
, опирающейся на этот контур, следовательно, поляризационным электрическим зарядом ![]()
![]() , индуцированным на указанной поверхности. Отсюда, в частности, следует определение поля вектора электрического смещения
, индуцированным на указанной поверхности. Отсюда, в частности, следует определение поля вектора электрического смещения ![]() , по величине равного плотности поляризационного заряда
, по величине равного плотности поляризационного заряда ![]() на пробной площадке, ориентация которой в данной точке создает на ней максимальное значение этого заряда, а нормаль к площадке указывает направление вектора
на пробной площадке, ориентация которой в данной точке создает на ней максимальное значение этого заряда, а нормаль к площадке указывает направление вектора ![]() . Определение
. Определение ![]() как потокового вектора показывает его принципиальное отличие от линейного (циркуляционного) вектора напряженности
как потокового вектора показывает его принципиальное отличие от линейного (циркуляционного) вектора напряженности ![]() , являющегося силовой характеристикой электрического поля.
, являющегося силовой характеристикой электрического поля.
Таким образом, согласно соотношению (5), электрическому заряду ![]() отвечает его полевой эквивалент - поле электрического векторного потенциала
отвечает его полевой эквивалент - поле электрического векторного потенциала ![]() , размерность которого есть линейная плотность электрического заряда. В итоге, с целью реализации нашего предположения введем понятие первой фундаментальной корпускулярно-полевой пары
, размерность которого есть линейная плотность электрического заряда. В итоге, с целью реализации нашего предположения введем понятие первой фундаментальной корпускулярно-полевой пары ![]()
![]()
![]() с единицами измерения в системе СИ Кулон
с единицами измерения в системе СИ Кулон![]() Кулон/метр.
Кулон/метр.
Здесь и далее обсуждаются именно размерности физических величин, а использование в рассуждениях конкретной системы единиц их измерения не принципиально.
Корпускулярно-полевые представления подтверждаются и соотношением (4) связи напряженности магнитного поля ![]() и электрического векторного потенциала
и электрического векторного потенциала ![]() с единицей измерения Ампер/метр, которое есть ни что иное, как полевой эквивалент полного электрического тока
с единицей измерения Ампер/метр, которое есть ни что иное, как полевой эквивалент полного электрического тока ![]() (токов проводимости и смещения), величина (сила тока) которого имеет единицу измерения Ампер. Как видим, сопоставление соотношения (4) для вихревых полей
(токов проводимости и смещения), величина (сила тока) которого имеет единицу измерения Ампер. Как видим, сопоставление соотношения (4) для вихревых полей ![]() и
и ![]() с понятием силы электрического тока снова приводит к корпускулярно-полевой паре Ампер
с понятием силы электрического тока снова приводит к корпускулярно-полевой паре Ампер![]() Ампер/метр, являющуюся очевидным прямым физическим следствием первой фундаментальной пары.
Ампер/метр, являющуюся очевидным прямым физическим следствием первой фундаментальной пары.
Перейдем теперь к магнитному векторному потенциалу и проанализируем соотношения связи поля вектора ![]() с полями векторов магнитной индукции
с полями векторов магнитной индукции ![]() (2a) и электрической напряженности
(2a) и электрической напряженности ![]() (3). Данные соотношения, несмотря на свою широкую известность [1, 2, 6], как нам представляется, трактуют не совсем корректно, поскольку в них исходно неверно определена размерность вихревого поля магнитного векторного потенциала импульс на единицу заряда. Попытаемся далее аргументировано обосновать это чрезвычайно серьезное, но пока декларативное критическое заявление о физической размерности вектора
(3). Данные соотношения, несмотря на свою широкую известность [1, 2, 6], как нам представляется, трактуют не совсем корректно, поскольку в них исходно неверно определена размерность вихревого поля магнитного векторного потенциала импульс на единицу заряда. Попытаемся далее аргументировано обосновать это чрезвычайно серьезное, но пока декларативное критическое заявление о физической размерности вектора ![]() .
.
Начнем с общеизвестного. Поскольку вектор электрической напряженности ![]() измеряется в системе СИ как Вольт/метр, либо математически (но не физически) тождественно Ньютон/Кулон, то, согласно соотношению (3) связи магнитного векторного потенциала
измеряется в системе СИ как Вольт/метр, либо математически (но не физически) тождественно Ньютон/Кулон, то, согласно соотношению (3) связи магнитного векторного потенциала ![]() с вектором
с вектором ![]() , единица измерения вектора
, единица измерения вектора ![]() будет (Ньютон·сек)/Кулон, то есть имеет размерность импульс на единицу заряда. Следовательно, соотношение (3) можно назвать полевым аналогом уравнения динамики поступательного движения в механике (II закон Ньютона). Действительно, указанную выше размерность магнитного векторного потенциала, другими словами, его физический смысл находят в работе [2] при анализе действия вихревого поля вектора
будет (Ньютон·сек)/Кулон, то есть имеет размерность импульс на единицу заряда. Следовательно, соотношение (3) можно назвать полевым аналогом уравнения динамики поступательного движения в механике (II закон Ньютона). Действительно, указанную выше размерность магнитного векторного потенциала, другими словами, его физический смысл находят в работе [2] при анализе действия вихревого поля вектора ![]() на точечный электрический заряд посредством именно II закона Ньютона, обычного механического. Однако обобщать такие выводы, полученные в рамках уравнения динамики поступательного движения, на случай макрообъекта (в виде совокупности взаимодействующих точечных зарядов), находящегося в вихревых полях, мягко говоря, весьма сомнительно.
на точечный электрический заряд посредством именно II закона Ньютона, обычного механического. Однако обобщать такие выводы, полученные в рамках уравнения динамики поступательного движения, на случай макрообъекта (в виде совокупности взаимодействующих точечных зарядов), находящегося в вихревых полях, мягко говоря, весьма сомнительно.
Для прояснения сложившейся ситуации рассмотрим далее соотношение (2а), которое представим для большей наглядности в интегральной форме:
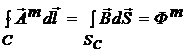 . (6)
. (6)
Видно, что величина циркуляции вектора ![]() по контуру С определяется магнитным потоком
по контуру С определяется магнитным потоком ![]() через поверхность SC и имеет единицу измерения в СИ Вебер = (Джоуль∙секунда)/Кулон, что соответствует модулю момента импульса на единицу заряда. При этом размерность магнитного векторного потенциала
через поверхность SC и имеет единицу измерения в СИ Вебер = (Джоуль∙секунда)/Кулон, что соответствует модулю момента импульса на единицу заряда. При этом размерность магнитного векторного потенциала ![]() может быть двоякой: либо указанная выше импульс на единицу заряда, либо ей альтернативная линейная плотность момента импульса на единицу заряда. Конечно, с формальной точки зрения обе размерности вектора
может быть двоякой: либо указанная выше импульс на единицу заряда, либо ей альтернативная линейная плотность момента импульса на единицу заряда. Конечно, с формальной точки зрения обе размерности вектора ![]() , выраженные через единицы измерения, математически тождественны, но физически это принципиально различные величины.
, выраженные через единицы измерения, математически тождественны, но физически это принципиально различные величины.
Целесообразно отметить, что сам Максвелл призывал ответственно относиться к математическим операциям над векторами электромагнитного поля и физической трактовке таковых. Вот его слова: “В науке об электричестве электродвижущая и магнитная напряженности принадлежат к величинам первого класса – они определены относительно линии. … Напротив, электрическая и магнитная индукция, а также электрические токи принадлежат к величинам второго класса – они определены относительно площади”. ([6] п. 12). И далее более конкретно: “В случае напряженности следует брать интеграл вдоль линии от произведения элемента длины этой линии на составляющую напряженности вдоль этого элемента. … В случае потоков следует брать интеграл по поверхности от потока через каждый ее элементов”. ([6] п. 14). Не преувеличивая, трактат Максвелла можно назвать физическими основами математического анализа, поскольку в нем свойства используемых математических моделей максимально подчинены стремлению автора адекватно описать физические представления о рассматриваемых явлениях. Однако, к сожалению, в настоящее время даже в учебной литературе повсеместно встречается “![]() ” и “
” и “![]() ”, “
”, “![]() ” и “
” и “![]() ”. Такое формальное использование математики попросту игнорирует физическое содержание соотношений электродинамики, создает путаницу физических понятий, мешая действительно разобраться в них. Все это усугубляется применением абсолютной системы единиц СГС, когда безразмерные коэффициенты e0 = 1 и m0 = 1 делают векторы
”. Такое формальное использование математики попросту игнорирует физическое содержание соотношений электродинамики, создает путаницу физических понятий, мешая действительно разобраться в них. Все это усугубляется применением абсолютной системы единиц СГС, когда безразмерные коэффициенты e0 = 1 и m0 = 1 делают векторы ![]() и
и ![]() ,
, ![]() и
и ![]() сущностно тождественными, где Эрстед и Гаусс равны в пустоте, а в средах различаются только численно. О предпочтительности в классической электродинамике международной системы единиц физических величин СИ в сравнении с абсолютной системой единиц СГС говорится также в работах [4, 5].
сущностно тождественными, где Эрстед и Гаусс равны в пустоте, а в средах различаются только численно. О предпочтительности в классической электродинамике международной системы единиц физических величин СИ в сравнении с абсолютной системой единиц СГС говорится также в работах [4, 5].
Для нас здесь существенно то, что, согласно Максвеллу, в электродинамике циркуляционные (линейные) векторы ![]() и
и ![]() имеют размерность линейной плотности физической величины, а потоковые векторы
имеют размерность линейной плотности физической величины, а потоковые векторы ![]() ,
, ![]() и
и ![]() – ее поверхностной плотности. В частности, размерность вектора магнитной индукции
– ее поверхностной плотности. В частности, размерность вектора магнитной индукции ![]() равна поверхностной плотности момента импульса на единицу заряда, в системе СИ Тесла. Экспериментально это ярко иллюстрируется эффектом Эйнштейна-де Гааза [1], где в материальной среде при ее однородном намагничивании возникает механический момент вращения, направленный коллинеарно полю, обусловленный упорядочением собственных магнитных моментов, соответственно, моментов количества движения электронов в атомах вещества среды. Следовательно, поле вектора
равна поверхностной плотности момента импульса на единицу заряда, в системе СИ Тесла. Экспериментально это ярко иллюстрируется эффектом Эйнштейна-де Гааза [1], где в материальной среде при ее однородном намагничивании возникает механический момент вращения, направленный коллинеарно полю, обусловленный упорядочением собственных магнитных моментов, соответственно, моментов количества движения электронов в атомах вещества среды. Следовательно, поле вектора ![]() выявляет в среде момент импульса, порождающий ее вращение. Поэтому, согласно соотношению (2а), размерностью вихревого поля магнитного векторного потенциала
выявляет в среде момент импульса, порождающий ее вращение. Поэтому, согласно соотношению (2а), размерностью вихревого поля магнитного векторного потенциала ![]() следует считать линейную плотность момента импульса на единицу заряда. Итак, в формулах (6) локальной характеристике микрочастицы моменту импульса на единицу заряда сопоставляется его полевой эквивалент магнитный векторный потенциал
следует считать линейную плотность момента импульса на единицу заряда. Итак, в формулах (6) локальной характеристике микрочастицы моменту импульса на единицу заряда сопоставляется его полевой эквивалент магнитный векторный потенциал ![]() , что дает вторую фундаментальную корпускулярно-полевую пару, которую, например, для электрона можно записать как
, что дает вторую фундаментальную корпускулярно-полевую пару, которую, например, для электрона можно записать как ![]() с единицами измерения (Джоуль∙секунда)/ Кулон
с единицами измерения (Джоуль∙секунда)/ Кулон![]() (Джоуль∙секунда)/(Кулон∙метр).
(Джоуль∙секунда)/(Кулон∙метр).
Вернемся к соотношению (3) связи вектора ![]() с вектором
с вектором ![]() . Как теперь здесь показано, размерность вихревого поля вектора электрической напряженности
. Как теперь здесь показано, размерность вихревого поля вектора электрической напряженности ![]() однозначно равна линейной плотности момента силы на единицу заряда, что естественно нисколько не опровергает единицу измерения этого вектора Вольт/метр, а лишь уточняет ее физический смысл. Таким образом, в действительности соотношение (3) представляет собой полевой аналог основного уравнения динамики вращательного движения твердого тела в механике, что полностью согласуется с рассмотренными выше корпускулярно-полевыми представлениями.
однозначно равна линейной плотности момента силы на единицу заряда, что естественно нисколько не опровергает единицу измерения этого вектора Вольт/метр, а лишь уточняет ее физический смысл. Таким образом, в действительности соотношение (3) представляет собой полевой аналог основного уравнения динамики вращательного движения твердого тела в механике, что полностью согласуется с рассмотренными выше корпускулярно-полевыми представлениями.
Подводя итог, с приходим к заключению, что векторные потенциалы – это не математические фикции, а фундаментальные первичные поля, поскольку именно они порождают традиционные вихревые электромагнитные поля в классической электродинамике. Важно при этом подчеркнуть, что с точки зрения проявления физических свойств [4, 5] рассматриваемые потенциалы логично называть поляризационными потенциалами. Установленная здесь принципиальная двойственность физических параметров электрического заряда говорит о реальном существовании «корпускулярно-полевого дуализма» природы электричества, у которого, в отличие от схожего лишь по названию «корпускулярно-волнового дуализма» в квантовой механике, континуальные компоненты являются векторным полем, и он реализуется на микро- и макроуровнях строения материи. Фундаментальность концепции указанного дуализма обусловлена тем, что локальные характеристики микрочастицы (совокупно, и макрообъекта) находятся в неразрывной связи с их собственными полевыми параметрами: электрическому заряду, кратному кванту электрического потока заряду электрона |e-|, соответствует электрический векторный потенциал ![]() , а ее удельному (на единицу заряда) кинетическому моменту, кратному кванту магнитного потока
, а ее удельному (на единицу заряда) кинетическому моменту, кратному кванту магнитного потока ![]() , отвечает магнитный векторный потенциал
, отвечает магнитный векторный потенциал ![]() . В качестве конкретной иллюстрации вышесказанного имеем из (5) и (6) для точечного заряда, например электрона, следующие выражения:
. В качестве конкретной иллюстрации вышесказанного имеем из (5) и (6) для точечного заряда, например электрона, следующие выражения: ![]() и
и ![]() . где
. где ![]() и
и ![]() орты сферической системы координат.
орты сферической системы координат.
Как видим, полученные результаты представляют общефизический интерес, требуют дальнейшего серьезного развития и, в частности, могут служить вместе с материалом работ [4, 5] непосредственным введением в новую перспективную область исследований связи полей классической электродинамики с микромиром.
Список литературы1. Матвеев А.Н. Электродинамика. - М.: Высшая школа, 1980. - 383 с.
2. Антонов Л.И., Миронова Г.А., Лукашёва Е.В., Чистякова Н.И. Векторный магнитный потенциал в курсе общей физики / Препринт № 11. - М.: Изд-во МГУ, 1998. - 47 с.
3. Патент РФ № 2101842. Способ обработки субстрата в поле магнитного векторного потенциала и устройство для его осуществления / В. Кропп.
4. Сидоренков В.В. Развитие физических представлений о процессе электрической проводимости в металле // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. - 2005. - № 2. - С. 35-46.
5. Сидоренков В.В. Обобщение физических представлений о векторных потенциалах в классической электродинамике // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. - 2006. - № 1. - С. 28-37.
6. Максвелл Дж. К. Трактат об электричестве и магнетизме. В 2-х томах. - М.: Наука, 1989.
Похожие работы
... и вносит в коды дополнения. Прямой луч формирует Высокочастотную Сферу неинерциального движения (ВЧС), обратный – Низкочастотную Сферу неинерциального движения (НЧС). Дуплекс движение каждого Тела КОСМОСа создает топологию Пространства – Времени Мироздания Мир – функция сознания систем. Вне всяких условий, Первоисток – Истина есть одна, и двух истин быть не может. Множество Лучей Со-Знаний, ...
0 комментариев