--------------------------------------------------------------------------¬ ¦ Корень n-й степени и его свойства. ¦ ¦Пример 1. ¦ ¦ Решим неравенство х6>20 ¦ ¦ Это неравенство равносильно неравенству х6-20>0. Так как функция ¦ ¦f(x)=х6-20 непрерывна, можно воспользоваться методом интервалов. ¦ ¦ 6| 6| ¦ ¦ Уравнение х6-20=0 имеет два корня : ? 20 и - ? 20 . Эти числа разби- ¦ ¦вают числовую прямую на три промежутка. Решение данного неравенства - ¦ ¦ 6| 6| ¦ ¦объединение двух из них : (-4; -? 20 ) (? 20 ;4) ¦ ¦ ¦ ¦Пример 2. 3| 5| ¦ ¦ Сравним числа ? 2 и ? 3 ¦ ¦ 3| 5| ¦ ¦ Представим ? 2 и ? 3 в виде корней с одним и тем же показателем: ¦ ¦ ¦ ¦ 3| 15| 15| 5| 15| 15| ¦ ¦ ? 2 = ? 25 = ?32 а ? 3 = ? 33 = ? 27 из неравенства ¦ ¦ 15| 15| 3| 5| ¦ ¦ 32 > 27 следует, что ?32 и ? 27 ,и значит, ? 2 > ? 3 ¦ +-------------------------------------------------------------------------+ ¦ Иррациональные уравнения. ¦ ¦ ¦ ¦ Пример 1. | ¦ ¦ Решим уравнение ? x2 - 5 = 2 ¦ ¦ Возведем в квадрат обе части уравнения и получим х2 - 5 = 4, отсюда ¦ ¦следует, что х2=9 х=3 или -3. ¦ ¦ Проверим, что полученные части являются решениями уравнения. ¦ ¦Действительно, при подстановке их в данное уравнение получаются верные ¦ ¦равенства | | ¦ ¦ ? 32-5 = 2 и ? (-3)2-5 = 2 ¦ ¦ ¦ ¦ Пример 2. | ¦ ¦ Решим уравнение ? х = х - 2 ¦ ¦ Возведя в квадрат обе части уравнения, получим х = х2 - 4х + 4 ¦ ¦После преобразований приходим к квадратному уравнению х2 - 5х + 4 = 0 ¦ ¦корни которого х=1 и х=4. Проверим являются ли найденные числа реше- ¦ ¦ниями данного уравнения. При подстановке в него числа 4 получаем вер- ¦ ¦ное равенство ?4 = 4-2 т.е. 4 - решение данного уравнения. При подста- ¦ ¦новке же числа 1 получаем в правой части -1, а в левой 1. Следователь- ¦ ¦но, 1 не является решением уравнения ; говорят, что это посторонний ¦ ¦корень, полученный в результате принятого способа решения . ¦ ¦ О Т В Е Т : Х=4 ¦ +-------------------------------------------------------------------------+ ¦ Степень с рациональным показателем. ¦ ¦ Пример 1. ¦ ¦ 3| 4| 4| ¦ ¦Найдем значение выражения 81/3 = ? 8 = 2 ; 813/4 = ? 813 = (?81)3= 33= ¦ ¦=27 ¦ ¦ ¦ ¦ Пример 2. ¦ ¦ Сравним числа 2300 и 3200 . Запишем эти числа в виде степени с ра- ¦ ¦циональным показателем : ¦ ¦ 2300 = (23)100 = 8100 ; 3200 = (32)100 = 9100 ¦ ¦ Так как 8<9 получаем : ¦ ¦ 8100 < 9100 т.е. 2300 < 3200 . ¦ ¦ ¦ L--------------------------------------------------------------------------
Раздел:
Математика Количество знаков с пробелами: 2445
Количество таблиц: 0
Количество изображений: 0
... дроби. Причем показано, что полученные таким образом ортогональные полиномы отвечают условиям метода наименьших квадратов, а так же показано их применение для нахождения кривых распределения вероятностей. § 1. Получение ортогональных полиномов по способу Чебышева. Пусть даны значения интерполируемой функции, соответствующие значения аргумента . Каждому значению аргумента ставится в соответствие ...
... задач с использованием различных модулей непрерывности. §1. Некоторые вспомогательные определения. В работе рассматриваются непрерывные функции f с периодом 2 и их приближение тригонометрическими полиномами. Через tn(x) обозначается тригонометрический полином порядка не выше n, а через tn*(x)=tn*(x,f)-тригонометрический полином, наименее уклоняющийся от f среди всех tn(x). Мы полагаем и ...
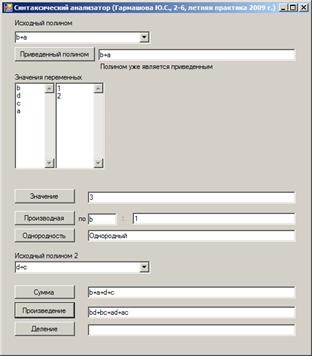
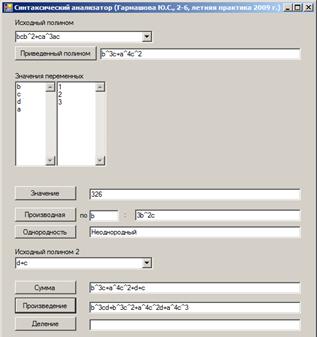
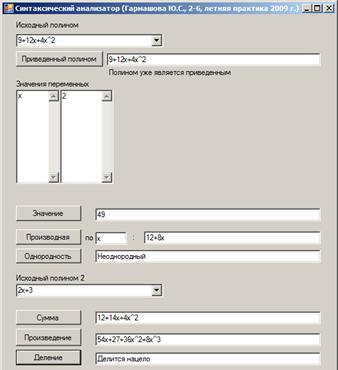
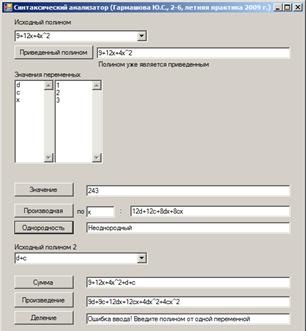
... на другой, очевидно, основано на операциях сложения и умножения полиномов. Поэтому для выполнения этого задания есть смысл воспользоваться процедурами сложения и умножения, описанных в пунктах 1.5 и 1.6. Глава 2. Реализация синтаксического анализатора полиномов в среде Visual Studio 2005 на языке C# Программа "Синтаксический анализатор" была написана на языке C# в среде Visual Studio 2005 ...
... о том, что, имея степень генерируемого полинома и его корни, мы можем с точностью до числового коэффициента определить и получить необходимый полином указанной степени. 1.2 Генерация полиномов Генерация достаточно молодая и полностью не исследованная область информатики и программирования. Дать точного и полного определения, что такое генерация пока еще не возможно. Под генерацией в ...



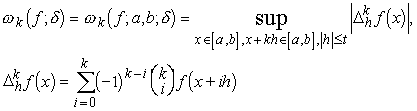
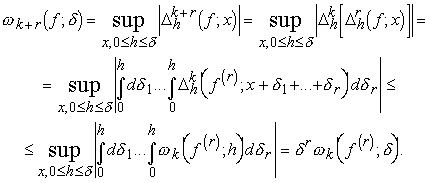
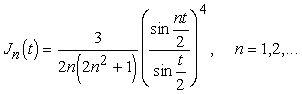

0 комментариев