Асп. Музаев Н.И.
Кафедра математики.
Северо-Кавказский горно-металлургический институт (государственный технологический университет
Составлена математическая модель волнового движения воды в узком глубоком непризматическом водохранилище с учетом упругости воды. Модель представляет начально-краевую задачу математической физики для потенциала средней по ширине векторной скорости. В основном дифференциальном уравнении начально-краевой задачи в качестве переменных коэффициентов содержится ширина водохранилища, зависящая от продольной и вертикальной координат. Составленная математическая модель позволяет решить широкий класс прикладных задач, связанных с теорией колебаний и волн в узких глубоких непризматических водохранилищах.
Предположим, что в прямоугольной системе координат xoyz часть пространства, ограниченная условиями 0 £ x £ l, – 1/2 B(x, z) £ y £ 1/2 B(x, z), –H £ z £ 0, представляет узкое глубокое непризматическое водохранилище. Ось oz направлена вертикально вверх, ось ox направлена в продольном, а ось oy – в поперечном направлении водохранилища. L – длина, B(x,z) – ширина, H – глубина водохранилища. Как правило, в горных условиях водохранилища строятся в узких глубоких каньонах ущелий рек. В связи с этим в дальнейшем будем считать, что ширина водохранилища B(x, z) намного меньше, чем ее длина. Кроме этого будем считать, что градиенты в поперечном направлении поля скоростей и гидродинамического давления намного меньше, чем градиенты в продольном и вертикальном направлении водохранилища. Ширина схематизированного водохранилища зависит от продольной и вертикальной координат B = B(x, z), т.е. рассматривается водохранилище с непризматической конфигурацией как в продольном, так и в вертикальном направлении. Для таких водохранилищ решение пространственной задачи волнового движения воды связано с большими математическими трудностями и в мире никем не решена.
В связи с этим трехмерные дифференциальные уравнения гидродинамики интегрально усредняют по площади живого сечения воды, в результате получают одномерные дифференциальные уравнения движения воды в естественных водоемах. В связи с тем, что водохранилища в горных местностях являются глубокими и узкими, то, в отличие от теоретической гидравлики, трехмерные уравнения гидродинамики мы интегрально усредняем только по поперечной координате y, а вертикальную координату оставляем без изменений.
В гидродинамике волнового движения жидкости дифференциальные уравнения используют в «отфильтрованном» виде, т.е. пренебрегают нелинейные члены как малые величины по сравнению с линейными членами. В проекциях на оси x, y и z эта система в «отфильтрованном» виде запишется так [1-3]:
; 
; 
; (1)
,
где приняты следующие обозначения: Vx , Vy и Vz – скорости в продольном, поперечном и вертикальном направлениях соответственно, зависящие от всех пространственных координат и времени t ; r – плотность; P – гидродинамическое давление; a – скорость звука в воде.
Усредним интегрально систему дифференциальных уравнений (1) по поперечной координате y.
; 
;
. (2)
.
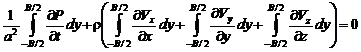Обратимся к известной формуле дифференцирования под знаком интеграла:
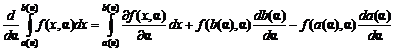. (3)
Интегралы, входящие в выражения (2), преобразуются так:
;
. (4)
В результате такого усреднения система~(2) запишется следующим образом:
; (5)
; (6)
, (7)
где приняты обозначения:
,
,
. (8)
Величины Ux , Uz и P представляют собой средние значения по ширине водохранилища соответственно Ux , Uz и P; q(x,z,t) – интенсивность боковой приточности, определяющаяся выражением:
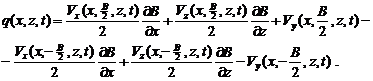(9)
Систему (5,6) в векторной форме можно записать так:
, (10)
, (11)
где 
.
Считая, что движение воды безвихревое, т.е. rot 
= 0, и вводя потенциал средней по ширине скорости
, (12)
из выражения (10) получаем интеграл Коши в линейном приближении:
. (13)
Компоненты средней скорости через потенциал скорости F(x, z, t) выражаются так:
, 
. (14)
В связи с тем, что потенциал скорости волнового движения жидкости определяется с точностью до произвольной функции, зависящей только от времени t, произвольную функцию f(t) можно считать тождественно равной нулю. На свободной волновой поверхности должно быть задано гидродинамическое давление 
. При отсутствии внешнего давления 
.
Обозначив уравнения волновой поверхности через z = h(x, t), выражение (13) запишется так:
. (15)
Линеаризуя выражение (15), получаем:
. (16)
В линейном приближении очевидно равенство:
. (17)
Дифференцируя выражение (16) по t и подставляя в него (17), получаем:
. (18)
Из выражения (13) при f(t) = 0 для давления получается следующая его зависимость от потенциала скорости:
. (19)
Подставив выражения (14) и (19) в (11), получим следующее дифференциальное уравнение для потенциала скорости:
. (20)
Как известно, в классической теории двумерного волнового движения упругой жидкости, для потенциала скорости имеется следующее уравнение [1,3]:
. (21)
Сравнивая уравнения (20) и (21), легко заметить, что в полученном в данной работе уравнении дополнительно содержатся три слагаемых. Последние две слагаемые в левой части учитывают непризматическое очертание водохранилища как в плане, так и по глубине. Величина q(x, z, t) представляет интенсивность вытеснения воды обвально-оползневым массивом либо интенсивность вторжения селелавинообразного потока в водохранилище.
Отметим, что в статье [4] получено дифференциальное уравнение для потенциала волнового движения несжимаемой жидкости в непризматическом водохранилище. В данной работе теория представляется более общей в связи с тем, что в ней учтена упругость воды, т.е. первое слагаемое уравнения(20).
Список литературы1. Ламб Г. Гидродинамика. М.: Гостехиздат, 1947.
2. Стокер Дж. Дж. Волны на воде. М.: Изд-во иностранной литературы, 1959.
3. Сретенский Л. Н. Теория волновых движений жидкости. М.: Наука, 1977.
4. Музаев И. Д., Созанов В. Г. К теории поверхностных гравитационных волн Коши – Пуассона в узких глубоких непризматических водоемах// Изв. вузов. Сев.-Кав. регион. Сер. ест. науки. Ростов-на Дону. 1995.
0 комментариев