Кодзодков А.Х.
Кафедра математического анализа.
Кабардино-Балкарский государственный университет
Рассмотрим линейное нагруженное уравнение третьего порядка:
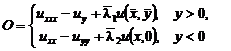 (1)
(1)
в – области ![]() , ограниченной отрезками
, ограниченной отрезками ![]() прямых
прямых ![]() соответственно при
соответственно при ![]() и характеристиками
и характеристиками ![]() ,
, ![]() уравнения (1) при
уравнения (1) при ![]() ;
; ![]() ;
; ![]() – интервал
– интервал ![]() ,
, ![]() – интервал
– интервал ![]() .
.
Здесь положено, что:
1) ![]()
или 2) ![]() .
.
Пусть имеет место случай (1).
Задача ![]() . Найти функцию
. Найти функцию ![]() со следующими свойствами: 1)
со следующими свойствами: 1) ![]() ;
;
2) ![]() – регулярное решение уравнения (1) при
– регулярное решение уравнения (1) при ![]() ;
;
3) ![]() удовлетворяет краевым условиям
удовлетворяет краевым условиям
![]() ,
, ![]() ; (2)
; (2)
![]() ,
,
![]() , (3)
, (3)
где ![]() ,
, ![]() – аффиксы точек пересечения характеристик уравнения (1) при y < 0, выходящих из точки
– аффиксы точек пересечения характеристик уравнения (1) при y < 0, выходящих из точки ![]() с характеристиками АС и ВС соответственно;
с характеристиками АС и ВС соответственно; ![]()
![]() ,
, ![]() ,
, ![]() .
.
Опираясь на однозначную разрешимость задачи Коши для уравнения (1) при y < 0 с начальными данными ![]() ,
, ![]() , легко видеть, что если существует решение задачи
, легко видеть, что если существует решение задачи ![]() , то оно представимо в виде:
, то оно представимо в виде:
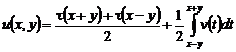 . (4)
. (4)
Учитывая (4) в краевом условии (3), получаем:
![]()
![]() , (5)
, (5)
где ![]() .
.
Следуя [1], обозначим через ![]() первообразную функции
первообразную функции ![]() . Тогда уравнение (5) примет вид:
. Тогда уравнение (5) примет вид:
![]()
![]() , (6)
, (6)
![]() , (7)
, (7)
где ![]() .
.
Относительно коэффициентов уравнения (6) будем рассматривать аналогичные ситуации, приведенные в работе [1]:
1) ![]() , т.е.
, т.е. ![]() ;
;
2) ![]() , , т.е.
, , т.е. ![]() ;
;
3)![]() , т.е.
, т.е. ![]() ;
;
4) ![]() ,
, ![]() , т.е.
, т.е. ![]() .
.
Пусть имеет место случай (1) и функции ![]() . Решение задачи (6), (7) в этом случае имеет вид:
. Решение задачи (6), (7) в этом случае имеет вид:
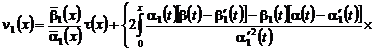
![]()
![]() , (8)
, (8)
где 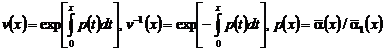 .
.
Дифференцируя равенство (8) и делая несложные преобразования, получаем:
![]()
![]() (9)
(9)
где ![]() ,
,
![]() ,
, 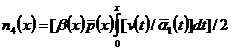 ,
,
![]() ,
,
![]()
![]() ,
, ![]() .
.
Переходя к пределу в уравнении (1) при ![]() , получаем функциональное соотношение между
, получаем функциональное соотношение между ![]() и
и ![]() , принесенное из области
, принесенное из области ![]() , на линию
, на линию ![]() :
:
![]() . (10)
. (10)
В силу граничных условий (2) и равенства (9) получим нелокальную задачу для нагруженного неоднородного интегро-дифференциального уравнения третьего порядка с переменными коэффициентами:
![]() , (11)
, (11)
![]() , (12)
, (12)
где ![]()
![]() .
.
В начале положим, что ![]() , т.е.
, т.е.
![]() ,
, ![]() , т.е.
, т.е.
![]() .
.
В зависимости от значений корней характеристического уравнения
![]() , (13)
, (13)
соответствующего однородному уравнению (11) (![]() ), будем исследовать разрешимость задачи (11), (12).
), будем исследовать разрешимость задачи (11), (12).
Введем обозначение ![]() . Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0.
. Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0.
Известно, что [2]: 1) если S>0, то уравнение (13) имеет только один действительный корень, а два остальных корня будут сопряженными чисто комплексными числами; 2) если S=0, то все три корня уравнения (13) действительны, причем два из них равны; 3) если S<0, то все три корня уравнения (13) действительны, причем все они различны.
Пусть S=0, т.е. ![]() .
.
Общее решение уравнения (11) в этом случае имеет вид:
![]() , (14)
, (14)
где ![]() ,
,
![]() .
.
Удовлетворяя (14) граничным условиям (12), получим линейную алгебраическую систему трех уравнений относительно ![]() с определителем:
с определителем:
![]() .
.
Положим, что ![]() . Тогда
. Тогда ![]() находят по формулам:
находят по формулам:
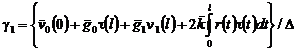 , (15)
, (15)
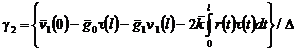 , (16)
, (16)
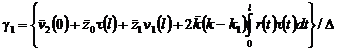 , (17)
, (17)
где 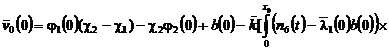
![]() ,
,
![]()
![]() ,
,
![]() ,
,
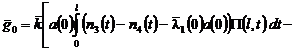
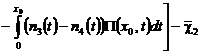 ,
,
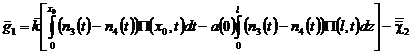 ,
,
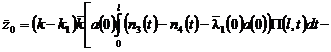
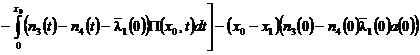 ,
,
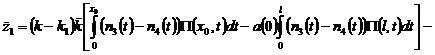
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Учитывая (15) – (17) в (14), получаем:
![]() ,
,
где ![]() ,
,
![]() ,
,
![]() ,
,
или
![]() , (18)
, (18)
где ![]() .
.
Если считать функцию ![]() известной, то (18) представляет собой интегральное уравнение Фредгольма второго рода с вырожденным ядром относительно
известной, то (18) представляет собой интегральное уравнение Фредгольма второго рода с вырожденным ядром относительно ![]() . Обозначив
. Обозначив
![]() ,
,
решение уравнения (18) будем искать в виде:
![]() . (19)
. (19)
После подстановки (19) в (18) имеем выражение:
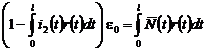 .
.
Если ![]() , то
, то ![]() определяется по формуле:
определяется по формуле:
![]() . (20)
. (20)
Учитывая (19), (20) в (18), получаем:
![]() , (21)
, (21)
где ![]() ,
,
![]() .
.
В равенстве (21) учтем значение ![]() . В результате будем иметь:
. В результате будем иметь:
![]()
![]() , (22)
, (22)
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
.
Перепишем уравнение (22) в виде:
![]() , (23)
, (23)
где ![]() .
.
В силу условий, наложенных на заданные функции ![]() , можем заключить, что
, можем заключить, что ![]() , следовательно
, следовательно ![]() .
.
Обращая интегральное уравнение Вольтерра второго рода (23), получаем:
![]() , (24)
, (24)
где ![]() – резольвента ядра
– резольвента ядра ![]() . Заметим, что резольвента
. Заметим, что резольвента ![]() обладает такими же свойствами, что и ядро
обладает такими же свойствами, что и ядро ![]() [3].
[3].
Заменяя в равенстве (24) функцию ![]() ее значением, получаем:
ее значением, получаем:
![]() , (25)
, (25)
где ![]() ,
,
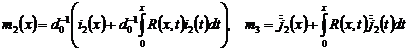 .
.
Перепишем уравнение (25) в виде:
![]() , (26)
, (26)
где ![]() .
.
Решение уравнения (26) будем искать в виде:
![]() , (27)
, (27)
где ![]() .
.
Поступая аналогично предыдущему случаю, получим
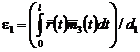 , если
, если ![]() .
.
Таким образом, имеем:
| 3 Труды молодых ученых № 3, 2007 |
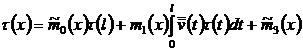 , (28)
, (28) где ![]() .
.
Уравнение (28) перепишем в виде:
![]() , (29)
, (29)
где ![]() .
.
Решение уравнения (29) ищем в виде:
![]() , (30)
, (30)
где ![]() .
.
Подберем теперь постоянную ![]() так, чтобы определенная формулой (30) функция
так, чтобы определенная формулой (30) функция ![]() была решением интегрального уравнения (29). С этой целью внесем выражение (30) для
была решением интегрального уравнения (29). С этой целью внесем выражение (30) для ![]() в левую часть (29). После простых вычислений получаем:
в левую часть (29). После простых вычислений получаем:
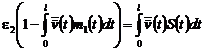 ,
,
откуда
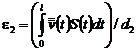 ,
,
где положено, что
![]() .
.
Таким образом, имеем:
![]() . (31)
. (31)
Полагая в равенстве ![]() , находим
, находим
![]() ,
,
если ![]() , т.е.
, т.е.
![]()
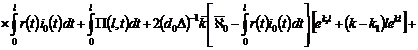
![]()
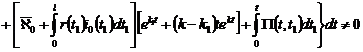 .
.
Пусть теперь имеет место случай 2), причем :
![]() .
.
В этом случае уравнение (6) принимает вид:
![]() , (32)
, (32)
где ![]() .
.
Учитывая условие (7), из (32) получаем соотношение ![]() ,
, ![]() . Подставляя это значение в (32), находим
. Подставляя это значение в (32), находим
![]() . (33)
. (33)
Подставляя (33) в (10), получаем нагруженное уравнение:
![]() , (34)
, (34)
где ![]() ,
,
![]() ,
,
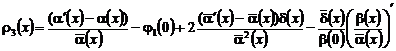 ,
,
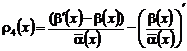
с внутренне-краевыми условиями (12).
Рассмотрим частный случай, когда ![]() , т.е.
, т.е.
![]() =
=![]() ;
; ![]() , т.е.
, т.е.
![]() ;
; ![]() , т.е.
, т.е.
![]() .
.
Тогда общее решение однородного уравнения
![]() имеет вид [4]:
имеет вид [4]:
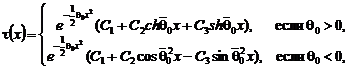
где ![]() .
.
Пусть ![]() . Методом вариации постоянных находим общее решение неоднородного уравнения (34) в виде:
. Методом вариации постоянных находим общее решение неоднородного уравнения (34) в виде:
![]() , (35)
, (35)
где ![]() ,
,
![]() .
.
Удовлетворяя (35) условиям (12), получаем:
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() ,
,
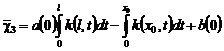 , причем выполняется условие
, причем выполняется условие
![]() , т.е.
, т.е. ![]() .
.
Равенство (35) перепишем в виде:
![]() , (36)
, (36)
где ![]() ,
, ![]() .
.
Из (36) при ![]() , имеем
, имеем
![]() ,
,
если выполняется условие ![]() , т.е.
, т.е.
![]() .
.
Пусть имеет место случай 3), причем ![]() ,
, ![]() . Тогда уравнение (6) принимает вид [1]:
. Тогда уравнение (6) принимает вид [1]:
![]() . (37)
. (37)
Полагая в равенстве (37) ![]() и, учитывая условия
и, учитывая условия ![]() , получим:
, получим:
![]() .
.
Следовательно, для ![]() имеем представление
имеем представление
![]()
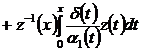 , (38)
, (38)
где ![]() .
.
Если выполняется условие 4) и функции ![]() , причем
, причем ![]() , то имеем равенство
, то имеем равенство
![]() . (39)
. (39)
Полагая в равенстве (39) ![]() и, учитывая условие
и, учитывая условие ![]() , находим
, находим
![]() .
.
Таким образом, имеем, что
![]() . (40)
. (40)
Полагая в равенствах (38), (40) ![]() , найдем
, найдем ![]() , а затем, подставляя их в равенство (10), однозначно найдем неизвестную функцию
, а затем, подставляя их в равенство (10), однозначно найдем неизвестную функцию ![]() .
.
Случай ![]() исследуется аналогично.
исследуется аналогично.
После определения функций ![]() решение задачи
решение задачи ![]() в области
в области ![]() задается формулой (4), а в области
задается формулой (4), а в области ![]() приходим к задаче (1), (2),
приходим к задаче (1), (2), ![]() .
.
Решение этой задачи дается формулой [5]:
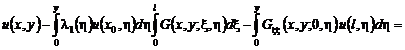
![]() , (41)
, (41)
где 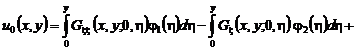
![]() .
.
Отсюда, полагая в равенстве (41) ![]() , получаем систему интегральных уравнений типа Вольтерра второго рода:
, получаем систему интегральных уравнений типа Вольтерра второго рода:
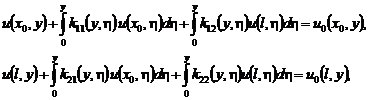 (42)
(42)
где ![]() ,
,
![]() .
.
В силу свойств функции ![]() и ядер системы (42), нетрудно убедиться, что система уравнений (42) допускает единственное решение в пространстве
и ядер системы (42), нетрудно убедиться, что система уравнений (42) допускает единственное решение в пространстве ![]() [3].
[3].
Наджафов Х.М. Об одной общей краевой задаче со смещением для уравнения Лаврентьева-Бицадзе // Известия КБНЦ РАН. Нальчик, №1(8), 2002.
Фадеев Д.К. Лекции по алгебре. М.1984.
Мюнтц Г. Интегральные уравнения. Л.-М., Т.1, 1934.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971.
Джураев Т.Б. Краевые задачи для уравнений смешанного и смешанно-составного типов. Ташкент: Фан, 1
Похожие работы
... на первой и последующих итерациях равна: ; (3.22) . (3.23) Критерием завершения итерационного процесса является условие: ,(3.24) где - заданная точность расчета [4]. 4. Методы оценки термонапряженного состояния 4.1 Физические основы возникновения термических напряжений При изменении температуры происходит объемное расширение или сжатие твердого тела. Неравномерный нагрев ...
... Роквеллу НR Число твердости по Бринеллю НВ, кгс/мм2 Лабораторная работа № 3 Методы исследования качества, структуры и свойств металлов и сплавов Цель работы 1. Изучить сущность, возможности и методику выполнения основных видов макроструктурного и микроструктурного ...
... В состав системы включены следующие интерфейсные программы: COSMOS/M DESIGNER. Автономная интерфейсная программа для системы AutoCAD. Она позволяет вызывать на выполнение вычислительные модули программы COSMOS/M прямо из среды AutoCAD через дополнительное меню. (AutoCAD продукция Autodesk, Inc.) COSMOS/M ENGINEER. Автономная интерфейсная программа для системы Рго/ENGINEER на рабочих станциях ...
... ; 12+φг)+ 2|S11Г0|cos(φ2+2φ12+2φг+ φ11)], (5.6) а условием баланса будет: (5.7) 6 РАЗРАБОТКА И ОПИСАНИЕ СТРУКТУРНОЙ СХЕМЫ УСТРОЙСТВА РВК На рисунке 6.1 представлена структурная схема устройства, предназначенного для контроля электрической толщины радиопрозрачных диэлектрических стенок методом свободного пространства на отражение с использованием модулирующего ...



0 комментариев