Эффективный алгоритм обращения матрицы Вандермонда

Доц. Кольвах В. Ф., инж. Кольвах Д. В.

Кафедра промышленной электроники.

Северо-Кавказский горно-металлургический институт (государственный технологический университет)

Разработан алгоритм, сочетающий точность и быстродействие, что позволяет рекомендовать его для практического использования.

Многие задачи расчета электронных схем, теории аппроксимации, теории прогнозирования и т. п. основаны на получении и обращении матрицы Вандермонда:

, (1)

Особый характер формирования столбцов матрицы v требует возведения в степень чисел сi . Если размер матрицы р достаточно велик, это приводит к плохой обусловленности матрицы. Например, для всех чисел |сi| >1 компоненты последующих строк будут много больше единицы, а для всех чисел |сi| < 1 эти компоненты оказываются много меньше единицы. Поэтому применение стандартных алгоритмов обращения не позволяет получить высокую точность из-за погрешностей обработки чисел в машине.

Существенно лучший результат достигается при использовании разработанной авторами и изложенной ниже последовательности операций.

1. На первом этапе находят общий характеристический многочлен:

. (2)

Обычно этот многочлен уже известен заранее из других этапов решения задачи получения матрицы v. В противном случае для его определения можно воспользоваться формулами Вьета [1] или следующей рекуррентной процедурой:

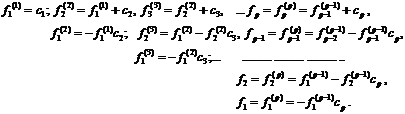 (3)

2. На втором этапе определяют частный характеристический многочлен для произвольной i-й строки матрицы v -1:

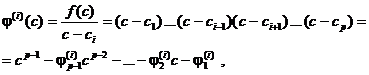 (4)

где

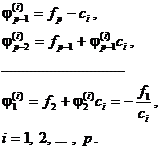
3. На третьем и заключительном этапе находят все элементы i-й строки искомой матрицы v -1 :

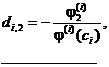 (5)

Следует отметить, что значение характеристического многочлена  и его коэффициенты  вычисляются один раз для всей строки с номером i.

Таким образом, матрица v -1 может быть представлена в следующем виде:

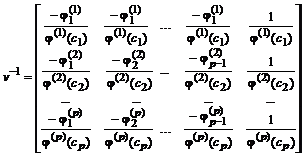 . (6)

Справедливость формулы (6) доказывается перемножением матриц vv -1 = v -1 v в общем виде. В результате получаем единичную матрицу.

Иногда требуется найти не всю матрицу v -1, а только одну из ее строк. В этом случае определение частного многочлена  рациональнее сразу проводить по формулам (3).

Изложенный алгоритм обеспечивает точное обращение матрицы Вандермонда при минимальном количестве операций перемножения-деления. Дополнительное сокращение объема вычислений достигается за счет того, что комплексно-сопряженные компоненты сi и сj исходной матрицы v дают в итоге комплексно-сопряженные строки в матрице v -1.

Следует отметить, что действительный столбец исходной матрицы v дает при обращении соответствующую действительную строку в матрице v -1, а умножение любого столбца на ненулевое число в матрице v приводит к делению на это же число соответствующей строки в матрице v -1 .

1. Курош А. Г. Курс высшей алгебры. М.: Наука, 1971.

2. Кольвах В. Ф., Кольвах Д. В. Расчет и оптимизация электронных схем. Владикавказ, СКГТУ, изд. "Терек", 1

Похожие работы

Система математических расчетов MATLAB

Скачать

249178

21

46

... системам линейных алгебраических уравнений с более чем одной неизвестной; MATLAB решает такие уравнения без вычисле-ния обратной матрицы. Хотя это и не является стандартным математическим обозначением, система MATLAB использует терминологию, связанную с обычным делением в одномерном случае, для описания общего случая решения совместной системы нескольких линейных уравнений. Два символа деления / ...