Навигация
Назовите точки, которые лежат на прямой, которые расположены над прямой, под прямой. .В .Г
1. Назовите точки, которые лежат на прямой, которые расположены над прямой, под прямой. .В .Г
![]() . З . А . Б . Д
. З . А . Б . Д
.И .Ж
Какие из этих точек будут лежать на прямой (принадлежать прямой), если её продолжить вправо, влево? Проверьте.
 Найдите лишнюю фигуру. Чем она отличается от всех остальных, почему она лишняя? (Последовательно рассматриваются ряды фигур а), б), в), г), д).)
Найдите лишнюю фигуру. Чем она отличается от всех остальных, почему она лишняя? (Последовательно рассматриваются ряды фигур а), б), в), г), д).)
а) б)
1 2 3 4 1 2 3 4
![]()
в) 1 2 3 4 г) 1 2 3 4
 д)
д)
1 2 3 4
Сначала линии в рядах не пронумерованы. Желательно их нарисовать разным цветом.
- посмотрите внимательно на эти линии (рассматриваем ряд а).). Найдите среди них одну линию, которая чем-то отличается от других. Чем она отличается? Каким признаком? Почему вы назвали ее лишней?
- какие линии нарисовал Карандаш? (прямые).
- сколько прямых линий он нарисовал? (показываем и считаем)
- какая по счету красная линия? (называют). Давайте обозначим её цифрой. (обозначают). Аналогичная работа проводится с остальными фигурами в рядах.
На доске или плакате рисуется несколько последовательностей лучей, например таких, какие изображены на рисунке ниже. С помощью вопросов типа: Что интересное заметили? Как меняется направление линий? и подобных детям предлагается найти закономерность в каждом ряде и продолжить этот ряд.
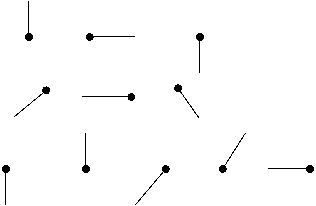
?
* * *
?
* * *
?
* * *
4. Соедините точки так, чтобы получились ступеньки. Как называется такая геометрическая фигура? (ломаная). Из скольких звеньев она состоит? Сколько ступенек находятся слева от зеленой? А сколько справа? Покажите ступеньки, которые выше зеленой ступеньки? Сколько ступенек ниже зеленой? и т.п.(звенья ломаной рисовать разным цветом)
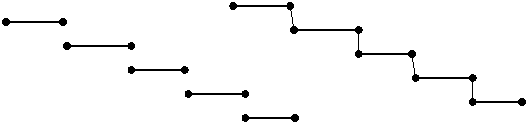
?
* * *
По какому правилу составлен каждый ряд фигур? Что изменяется? Продолжите ряд по тому же правилу. Какая из нижних фигур а), б), в) или г) будет следующей в каждом случае?
А)
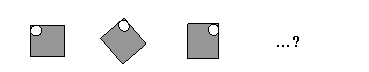
1. 2. 3. 4.
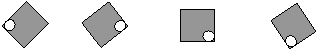
а) б) в) г)
| …? |
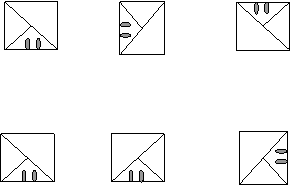 Б)
Б) …?
1. 2. 3. 4.
а) б) в)
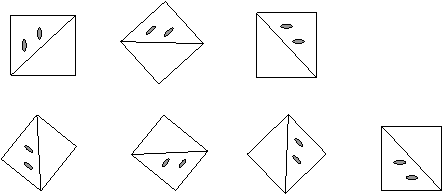 В)
В)
…?
1. 2. 3. 4.
а) б) в) г)
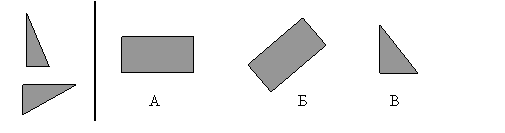
6. Задачи на превращения геометрических фигур. На первом этапе работы с такими задачами ученики выполняют задания, используя фигуры, вырезанные из цветного картона. На втором этапе, после приобретения соответствующих навыков, задания выполняются мысленно с последующей проверкой верности своего выбора путем сбора фигуры. В качестве образцов таких заданий можно предложить следующие:
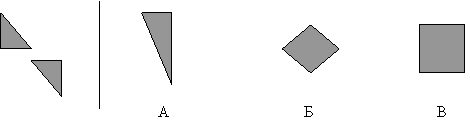
Какую фигуру справа можно получить при складывании данных частей, расположенных слева;
Как называются выбранные вами фигуры? Чем они похожи? Чем отличаются?
Какие еще фигуры можно собрать из двух фигур, изображенных слева? и т.д.
а)
 б)
б)
в)
Ответы: а) Фигуру А и фигуру Б; прямоугольники одинакового размера; взаимным расположением на плоскости.
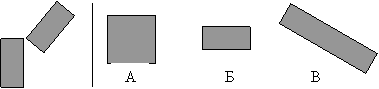
б) фигуру А и фигуру В; четырехугольники; А – квадрат, В – прямоугольник.
в) фигуру Б и фигуру В; общее – квадраты; отличия – фигура Б повернута относительно фигуры В на 90о. Можно получить и такие фигуры:

7. Задания на подборку фигуры заданной формы и размера, типа «Подбери заплатку». Задания выполняются путем логического мышления; предположения тетей проверяются практически, так как все детали съёмные.
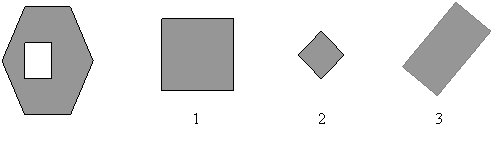 а)
а)
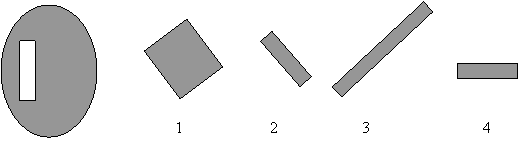 б)
б)
Ответы: а) 2; б) 2, 4.
По мнению этих же авторов достаточно большое значение в формировании пространственных представлений младших школьников имеет организация работы по ориентации плоских и объемных геометрических фигур. С этой целью предлагается использование серий упражнений на соответствие образа (модели) и его изображения с учетом переориентации на плоскости и в пространстве на основе простой формы ориентировки по «схеме тела».
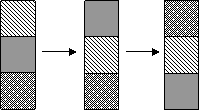 Так в задании «Что изменилось? Что не изменилось?» выстраиваются в ряд различные по цвету прямоугольники, которые меняют положение в пространстве в вертикальном направлении, что описывается отношениями «вверху – внизу», «между».
Так в задании «Что изменилось? Что не изменилось?» выстраиваются в ряд различные по цвету прямоугольники, которые меняют положение в пространстве в вертикальном направлении, что описывается отношениями «вверху – внизу», «между».
В задании «Раскрась фигуру справа» из нижнего ряда следует выбрать квадрат, имеющий такой же рисунок, как и исходный, но изменивший свое положение при повороте его вверх на один оборот; это упражнение одновременно с развитием пространственной ориентации закрепляет такие понятия, как «справа – слева». Это квадрат 2.
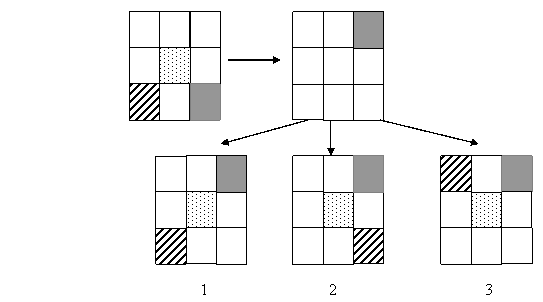
В заданиях типа «Чем похожи? Чем отличаются?» формируются и развиваются пространственные связи «слева – справа», «сверху – снизу», «повернуть вправо – повернуть влево» и т.п:
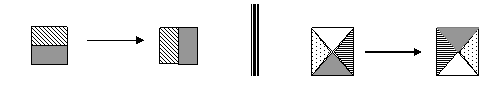
4. В заданиях типа «Выбери фигуру, которую нужно дорисовать» предполагается формирование умений осуществлять поворот вправо, влево, вверх или вниз на один или несколько оборотов. В предлагаемом ниже упражнении осуществляется поворот «вверх – влево», при котором круг, расположенный внизу, перемещается вправо.
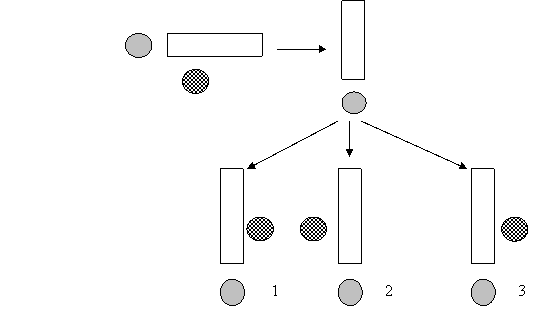
Аналогичные задания – упражнения можно производить и с другими геометрическими фигурами, а также с рисунками. Большие возможности для проведения таких упражнений предоставляются, если использовать на уроках математики кубики из детского конструктора, а при отсутствии таковых – обычные деревянные кубики, которые можно сделать в школьных мастерских. Делая пометки на одной или двух гранях кубика в виде точек разного цвета или окрашивая их в разные цвета, можно составить целые серии упражнений разной направленности и разного уровня сложности для формирования и развития пространственных представлений учеников начального звена обучения. Эти серии можно условно разделить на несколько групп по степени сложности и глубине формирования пространственных представлений у учащихся:
1 группа. «Оперирование моделью кубика». Располагая кубик к ученику фронтальной гранью с пометкой, можно выполнить такие упражнения:
а) кубик повернули на один оборот влево. Какое положение займет модель кубика? Найди это положение на чертеже?
б) поверни модель кубика так, чтобы он занял указанное на чертеже положение. И т.д.
2 группа. «Оперирование образом в фиксированной системе отсчета, совпадающей со «схемой тела».
Осуществляются повороты кубика на один оборот вправо (влево) в строго фиксированной фронтальной системе отсчета. Оперирование пространственным образом происходит в результате перекодировки образа, то есть перехода из трехмерного пространства в двумерное путем вычленения плоского элемента объемной формы. Ребенок осуществляет мысленное вращение не самого кубика а лишь его передней грани.
Не описывая подробно механизм выполнения упражнений, можно выделить еще две группы подобных заданий:
Похожие работы
... . Так. если единицей объёма является 1 см, то объём фигуры, приведённой на рисунке 7, равен 4 см. ГЛАВА 2.Методика формирования понятия величины и её измерения у младших школьников. 2.1 Современные подходы к изучению величин в начальном курсе математики. В начальных классах рассматриваются такие величины, как: длина, площадь, масса, объём, время и ...
... натурального ряда. В качестве графической модели используем числовой луч, на котором дети отмечают точки, соответствующие натуральным числам. Смысл действий сложения и вычитания. В курсе математики начальной школы находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел, в соответствии с которым сложение связано с операцией объединения, ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
... . При изучении нового материала рекомендуется такое построение урока, при котором работа начинается с разнообразных демонстраций, проводимых учителем или учеником. Применение наглядности на уроках математики при изучении геометрического материала, позволяет прочно и сознательно усвоить детям все программные вопросы. Язык математики – это язык символов, условных знаков, чертежей, геометрических ...
0 комментариев