5. Рассчитать частотные характеристики цепи
Для выполнения расчета необходимо:
– определить комплексный коэффициент передачи по напряжению исследуемой цепи
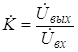 , (1.1)
, (1.1)
где 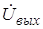 и
и 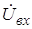 - комплексные амплитуды выходного и входного напряжений;
- комплексные амплитуды выходного и входного напряжений;
– рассчитать амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ) характеристики;
– построить графики АЧХ и ФЧХ.
2. курсовая работа
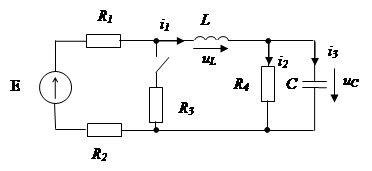
Рассмотрим пример выполнения задания курсовой работы для схемы, приведенной на рис. 3.1 со следующими исходными данными: Em = 10 В, Re = 104 Ом, R1 = R2 = R3 = R = 2·103 Ом, C1 = C2 =1 нФ, ω = 105 рад/с.
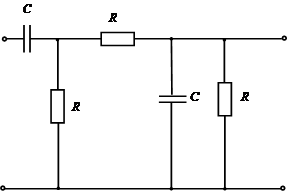
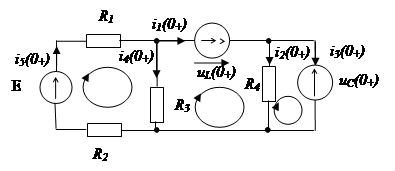
Рис. 2.1 Схема исследуемой цепи 2.1 Составление схемы исследуемой цепи В соответствии с п. 1 задания к курсовой работе ко входу схемы необходимо подключить источник э.д.с. с внутренним сопротивлением (т.е. дорисовать слева к имеющейся схеме условно-графическое обозначение источника э.д.с. и сопротивления), произвести нумерацию элементов (слева направо, сверху вниз) и расставить токи. Выбор направлений протекания токов во всех ветвях определяется в зависимости от направления э.д.с. После указанных действий исходная схема преобразуется к виду, приведенному на рис. 2.2.
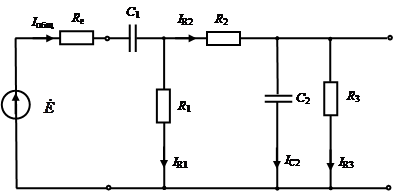
Рис. 2.2. Преобразованная схема исследуемой цепи 2.2 Расчет токов и напряжений в элементах цепи Расчет в данной схеме целесообразно начать с простого соединения двух элементов R
3 и C
2. Комплексное сопротивление этого участка цепи как любого параллельного соединения (см. формулу (2.19)) равно
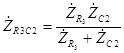
, (3.1) где комплексное сопротивление
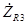
активного сопротивления R
3 равно самому этому сопротивлению (
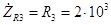
Ом), а комплексное сопротивление
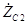
емкости С
2 равно
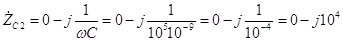
Ом. (3.2) Поэтому, подставляя эти значения в (3.1), получаем, что комплексное сопротивление параллельного участка цепи R
3 C
2 равно
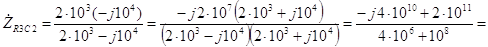
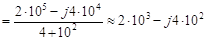
Ом. (3.3) В дальнейшем, при нахождении токов и напряжений элементов цепи, необходимо будет применять закон Ома в комплексной форме, а следовательно, придется делить и умножать комплексные величины. Это удобнее делать если числа будут представлены в показательной форме. Для перевода числа в показательную форму необходимо найти его модуль и аргумент. Модуль полученного в (3.3) комплексного числа равен
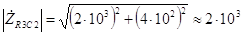
Ом, (3.4) а аргумент
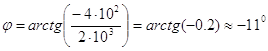
. (3.5) Поэтому комплексное сопротивление участка R
3C
2 можно записать, как
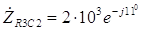
Ом. Участок цепи R
2R
3C
2 представляет собой последовательное соединениесопротивления R
2 параллельного соединения элементов R
3C
2. Поэтому комплексное сопротивление всего участка R
2R
3C
2 равно
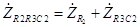
. (3.6) Комплексное сопротивление
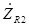
активного сопротивления R
2 равно самому этому сопротивлению (
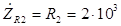
Ом). Следовательно, комплексное сопротивление рассматриваемого участка в соответствии с (3.3) и (3.6) можно определить по формуле
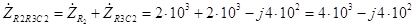
Ом. (3.7) Точно также, как и в предыдущем случае, полученный результат целесообразно сразу преобразовать в экспоненциальную форму. Для этого необходимо найти модуль и аргумент. Модуль полученного в (3.7) комплексного числа равен
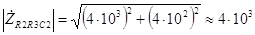
Ом, (3.8) а аргумент
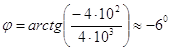
. (3.9) Поэтому комплексное сопротивление участка цепи можно записать, как
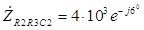
Ом. Сопротивление R
1 подключено к участку цепи R
2R
3C
2 параллельно. Следовательно, комплексное сопротивление этого участка цепи как любого параллельного соединения равно
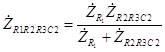
, (3.10) Комплексное сопротивление
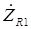
активного сопротивления R
1 равно самому этому сопротивлению (
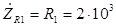
Ом). Следовательно, комплексное сопротивление рассматриваемого участка R
1R
2R
3C
2 можно рассчитать по формуле
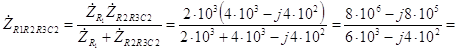
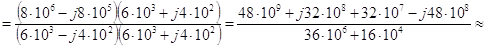
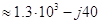
Ом. (3.11) Аналогично предыдущему случаю для перевода числа в показательную форму необходимо найти модуль и аргумент. Модуль полученного комплексного числа равен
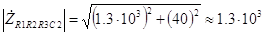
Ом, (3.12) а аргумент
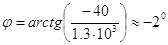
. (3.13) Поэтому искомое комплексное сопротивление участка цепи R
1R
2R
3C
2 можно записать, как
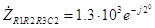
Ом. Всю рассматриваемую цепь можно представить как последовательное соединение (см. рис. 3.2)сопротивления R
е, емкости С
1 и участка цепи R
1R
2R
3C
2. Поэтому полное комплексное сопротивление всей цепи равно
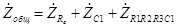
. (3.14) Комплексное сопротивление
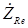
активного сопротивления R
е равно самому этому сопротивлению (
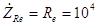
Ом), а следовательно, учитывая (3.11), комплексное сопротивление всей цепи можно рассчитать по формуле
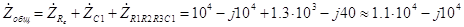
Ом. (3.15)
Модуль полученного комплексного числа равен
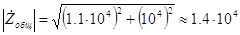
Ом, (3.16) а аргумент равен
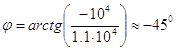
. (3.17) Поэтому полное комплексное сопротивление всей цепи можно записать как
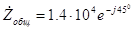
Ом. При изучении исследуемой цепи, как уже было отмечено выше, видно, что элементы R
e, С
1 и участок цепи R
1R
2R
3C
2 соединены последовательно, и как следует из определения последовательного соединения, через них протекает один и тот же ток, т.е. общий ток цепи, протекающий через источник э.д.с., равен
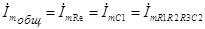
. (3.18) В соответствии с законом Ома в комплексной форме для участка цепи (2.9) этот ток может быть рассчитан как отношение комплексной амплитуды э.д.с. к комплексному сопротивлению всей цепи, т.е. как
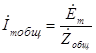
. (3.19) Комплексная амплитуда э.д.с. в общем виде в показательной форме может быть записана как
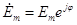
. Как следует из исходных данных, аргумент в данном случае равен нулю (φ = 0), а модуль равен E
m = 10 В, т.е.
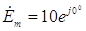
. Таким образом, комплексная амплитуда общего тока цепи может быть рассчитана по формуле
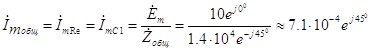
А . (3.20) Напряжение на сопротивлении R
e равно произведению комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е.
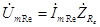
. (3.21) Подставляя в (3.21) полученное в (3.20) выражение, а также с учетом того, что комплексное сопротивление
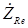
активного сопротивления R
е равно самому этому сопротивлению (
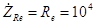
Ом), получаем, что
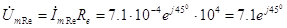
В . (3.22) Напряжение на емкости С
1 может быть рассчитано как произведение комплексной амплитуды
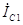
протекающего через нее тока на комплексное сопротивление этого элемента, которое по аналогии с (3.2) равно
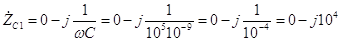
Ом. (3.23) Следовательно, напряжение на емкости С
1 равно
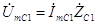
. (3.24) Подставляя полученные в (3.20) и (3.23) числовые данные, получаем, что
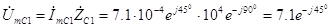
В. (3.25) Точно таким же образом можно определить напряжение на участке цепи R
1R
2R
3C
2. Его комплексная амплитуда равна произведению комплексной амплитуды протекающего через нее тока
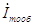
на комплексное сопротивление этого участка, т.е. с учетом (3.11) и (3.20)
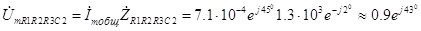
В. (3.26) При определении напряжения на сопротивлении R
1 необходимо учитывать, что
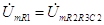
, т.е. так как соединение R
1 и R
2R
3C
2 параллельное, то
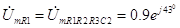
В. (3.27) Комплексная амплитуда тока, протекающего через сопротивление R
1, равна отношению комплексной амплитуды напряжения к комплексному сопротивлению элемента. Так как, как было замечено выше, для активного сопротивления
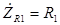
, ток можно рассчитать по формуле
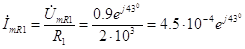
А . (3.28)
Аналогично предыдущему случаю, комплексная амплитуда тока, протекающего через участок цепи R
2R
3С
1, равна отношению комплексной амплитуды напряжения на этом участке к полному комплексному сопротивлению участка. Эти величины уже были найдены ранее в (3.7) и (3.26). Поэтому
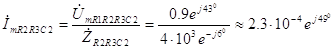
А . (3.29) Как и было показано выше, напряжение на активном сопротивлении R
2 может быть определено как произведение комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е. как
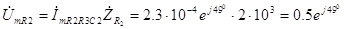
В. (3.30) Аналогично (3.30), напряжение на участке цепи R
3C
2 равно произведению комплексной амплитуды
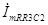
протекающего через нее тока на комплексное сопротивление этого участка, т.е.
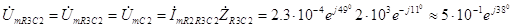
В.(3.31) Комплексная амплитуда тока, протекающего через емкость C
2, равна отношению комплексной амплитуды напряжения к комплексному сопротивлению элемента:
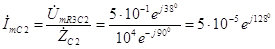
А. (3.32) Комплексная амплитуда тока, протекающего через емкость R
3, равна
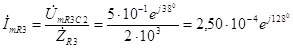
А. (3.33) Полученные результаты заносятся в таблицу, аналогичную приведенной в задании.
Таблица 3.1 – Результаты расчета токов и напряжений в элементах цепи
| | Номинал | Um, В | Im, мкА | ψU, град. | ΨI, град. |
| Re | 104 Ом | 7.1 | 710 | 45 | 45 |
| R1 | 2·103 Ом | 0.9 | 450 | 43 | 43 |
| R2 | 2·103 Ом | 0.5 | 230 | 49 | 49 |
| R3 | 2·103 Ом | 0.5 | 250 | 38 | 38 |
| C1 | 1·10-9 Ф | 7.1 | 710 | -45 | 45 |
| C2 | 1·10-9 Ф | 0. 5 | 50 | 38 | 128 |
2.3 Проверка результатов с помощью законов Кирхгофа Для проверки результатов вычислений с помощью первого закона Кирхгофа необходимо проверить насколько точно выполняется соотношение, определяемое этим законом, а именно: сумма входящих в узел токов равна сумме выходящих токов. Так как в цепи присутствуют реактивные элементы, то все расчеты и величины при этом используются в комплексной форме. Применительно к рассматриваемой схеме для верхнего левого узла должно выполнять соотношение
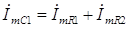
(3.34) или в числовом виде
7,1·10
-4·e
j45 = 4,5·10
-4·e
j43 + 2,3·10
-4·e
j49 . (3.35) Рассчитаем значение выражения в правой части. Для перехода от показательной формы к нормальной используется следующее математическое правило: действительная часть равна произведению модуля на косинус аргумента, а мнимая – произведению модуля на синус аргумента, т.е. в общем виде для произвольного комплексного числа в показательной форме
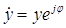
можно записать:
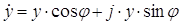
. (3.36) Для рассматриваемого примера в числовой форме:
4,5·10
-4·e
j43 + 2,3·10
-4·e
j49 =4,5·10
-4·cos(43
0) + j4,5·10
-4·sin(43
0) +
+ 2,3·10
-4 ·cos(49
0) + j2,3·10
-4·sin(49
0) = 3,3·10
-4 + j3,1·10
-4 +1,5·10
-4 +
+ j1,7·10
-4 = 4,8·10
-4 – j4,8·10
-4 ≈ 6,7·10
-4 ·e
j45 . (3.37) Таким образом, получается, что должно выполняться соотношение
7,1·10
-4·e
j45 = 6,7·10
-4 ·e
j45. (3.38) Как видно из (3.38), аргументы обоих чисел точно равны друг другу, а модули отличаются на 6 %, что можно рассматривать как небольшую погрешность. Аналогичным образом может быть проверено выполнение первого закона Кирхгофа и для остальных узлов. Для проверки результатов с помощью второго закона Кирхгофа необходимо проверить насколько точно выполняется соотношение, определяемое этим законом, а именно: для левого контура цепи должно выполнять соотношение
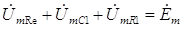
(3.39) или в числовом виде
7,1·e
j45 + 7.1·e
-j45 + 0.9·e
j43 = 10· e
j0. (3.40) Для суммирования в левой части этого выражения необходимо произвести преобразование чисел из показательной в нормальную форму: 7,1·e
j45 + 7,1·e
-j45 + 0,9·e
j43 = 7,1·cos(45
0) + j7,1·sin(45
0) + 7,1·cos(45
0) – – j7,1·sin(45
0) + 0,9·cos(43
0) + j0,9·sin(43
0) = 10,7 + j0,6 ≈ 7,1·e
j3. (3.41) Таким образом, должно выполняться соотношение 7,1·e
j3 = 10·e
j0. (3.42) Как видно из (3.40), левые и правые части этого выражения приблизительно равны друг другу. Аналогичным образом может быть проверено выполнение второго закона Кирхгофа и для остальных независимых контуров. Рассмотрев выполнение обоих законов Кирхгофа, можно сделать вывод о правильности произведенных расчетов токов и напряжений на элементах цепи. 2.4 Построение полной векторной диаграммы цепи Построение векторной диаграммы цепи производится на основе числовых данных, представленных в таблице. Для каждого тока (напряжения) в таблице имеются значения модуля и аргумента. Например, модуль напряжения на сопротивлении R
e равен 7,1 В, а аргумент равен 45
0. Следовательно, вектор, соответствующий
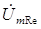
, будет иметь длину 7,1 (или другую в соответствии с выбранным масштабом) и угол относительно горизонтальной оси 45
0 (рис. 3.3). Аналогичным образом строятся векторы, соответствующие остальным токам и напряжениям, приведенным в таблице. При этом все построения начинаются из одной точки и угол откладывается в одном направлении. После построения всех векторов, соответствующих токам и напряжениям на элементах цепи, необходимо провести вектор, соответствующий комплексной амплитуде источника э.д.с., воздействующего на цепь. Для того, чтобы рисунок не был сильно загроможденным построения проведены раздельно на разных плоскостях для напряжений и токов, как это сделано на рис. 3.4 и рис. 3.5 применительно к рассматриваемой схеме рис. 3.2.

Рис. 3.3. Построение вектора комплексной амплитуды

Рис. 3.4. Векторная диаграмма напряжений
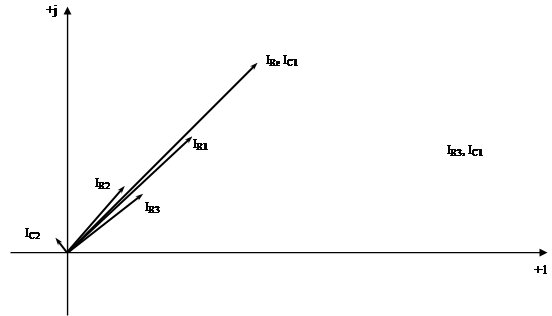
Рис. 3.5. Векторная диаграмма токов
2.5 Расчет частотных характеристик цепи Для нахождения частотных характеристик цепи возможно применение как аналитического расчета, так и использование специализированных программ моделирования электрических цепей, например, Electronic Work Bench. Рассмотрим первый вариант.
При проведении аналитического расчета частотных характеристик возможно два варианта:
1. вывод формулы для расчета частотных характеристик в общем виде, а затем подстановка в них значений частот При этом необходимо получить в общем виде выражение, соответствующее выходному напряжению цепи, т.е. зависимость 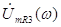 . Для этого повторяются все расчеты (3.1) – (3.33) не подставляя в формулы числовое выражение частоты ω. В результате этого поучится выражение, содержащее зависимость от частоты;
. Для этого повторяются все расчеты (3.1) – (3.33) не подставляя в формулы числовое выражение частоты ω. В результате этого поучится выражение, содержащее зависимость от частоты;
2. расчет частотных характеристик по нескольким точкам. В качестве одной из них можно использовать точку с частотой, равной заданной по варианту, а значение второй частоты можно выбрать произвольно и для нее повторить все вычисления с самого начала.
Остановимся на последнем варианте как на более простом. Рассмотрим в начале две крайние точки: при частоте, равной нулю, и при частоте, стремящейся к бесконечности.
В первом случае как следует из формулы реактивного сопротивления емкости, реактивное сопротивление С
1 будет стремиться к бесконечности, а следовательно, общий ток цепи, а соответственно и напряжение на выходе схемы (на сопротивлении R
3), будет равен нулю. Это означает, что коэффициент передачи цепи при в этом случае равен нулю. Во втором случае (при частоте, стремящейся к бесконечности) сопротивление емкости С
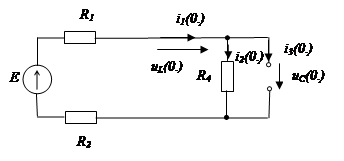
1 будет стремиться к нулю. При этом исходная схема (рис. 3.2) преобразуется к виду, представленному на рис. 3.6.
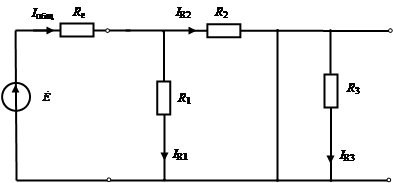
Рис. 3.6. Исходная схема при частоте э.д.с., стремящейся к нулю Как видно из данного рисунка, выход схемы по существу «закорочен», а следовательно, напряжение на выходе будет равно нулю. Таким образом, коэффициент передачи цепи в обоих рассмотренных случаях равен нулю.
При частоте, равной приведенной в задании, коэффициент передачи цепи равен
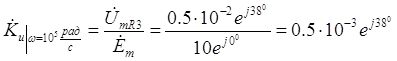
. (3.43) Рассмотрим еще одну точку частотной характеристики, например, соответствующую частоте ω = 10
3 рад/с. Для этого повторим расчеты (3.1) – (3.33) при новом значении частоты. Комплексное сопротивление
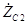
емкости С
2 так же, как и С
1, равно
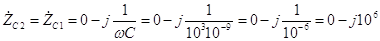
Ом. (3.44)
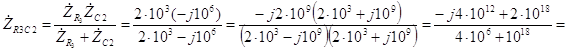
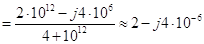
Ом. (3.45)
Модуль полученного комплексного числа равен
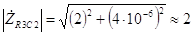
Ом, (3.46) а аргумент
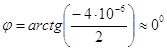
. (3.47) Поэтому искомое комплексное сопротивление участка цепи можно записать, как
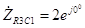
Ом. Комплексное сопротивление всего участка R
2R
3C
2 участка цепи равно
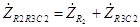
. (3.48) Комплексное сопротивление
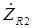
активного сопротивления R
2 равно самому этому сопротивлению (
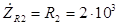
Ом). Следовательно, комплексное сопротивление участка R
2R
3C
2 в соответствии с (3.45) и (3.48) можно рассчитать по формуле
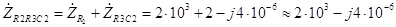
Ом. (3.49) Модуль полученного комплексного числа равен
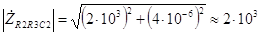
Ом, (3.50) а аргумент равен
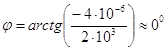
. (3.51) Поэтому искомое комплексное сопротивление участка цепи можно записать, как
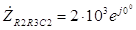
Ом. Комплексное сопротивление участка R
1R
2R
3C
2 можно рассчитать по формуле
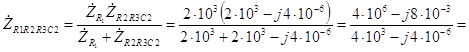
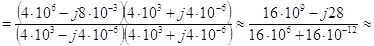
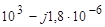
Ом. (3.52) Модуль полученного комплексного числа равен
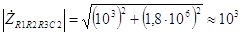
Ом, (3.53) а аргумент
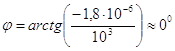
. (3.54) Поэтому искомое комплексное сопротивление участка цепи R
1R
2R
3C
2 можно записать, как
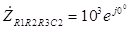
Ом. Комплексное сопротивление всей цепи можно рассчитать по формуле
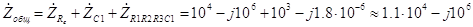
Ом. (3.55) Модуль полученного комплексного числа равен
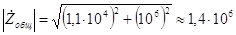
Ом, (3.56) а аргумент равен
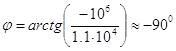
. (3.57) Поэтому полное комплексное сопротивление всей цепи можно записать как
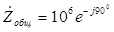
Ом. Общий ток цепи может быть рассчитан по формуле
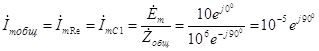
А. (3.58) Для участка цепи напряжение на сопротивлении R
e может быть рассчитано как произведение комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е.
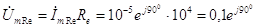
В. (3.59) Напряжение на емкости С
1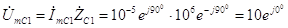
В. (3.60) Напряжение на участке цепи R
1R
2R
3C
2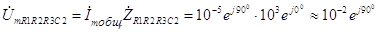
В. (3.61) Напряжение на сопротивлении R
1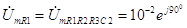
В. (3.62) Комплексная амплитуда тока, протекающего через сопротивление R
1, равна отношению комплексной амплитуды напряжения к комплексному сопротивлению элемента. Так как, как было замечено выше, для активного сопротивления
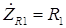
, ток можно рассчитать по формуле
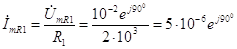
А. (3.63) Комплексная амплитуда тока, протекающего через участок цепи R
2R
3С
1, равна
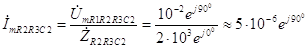
А. (3.64) Напряжение на R
е может быть определено как
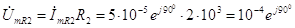
В. (3.65) Напряжение на участке цепи R
3C
2 произведению комплексной амплитуды
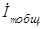
протекающего через нее тока на комплексное сопротивление этого участка, т.е.
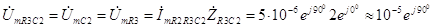
В. (3.66) Таким образом, коэффициент передачи по аналогии с (3.41) для частоты ω = 10
3 рад/с равен
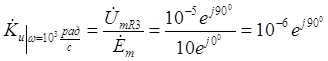
. (3.67) На рис. 3.7 и рис. 3.8 представлены графики амплитудно- и фазочастотных характеристик рассматриваемой схемы, полученные аналитическим путем.
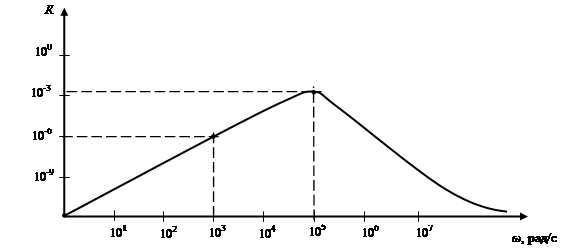
Рис. 3.7. Амплитудно-частотная характеристика
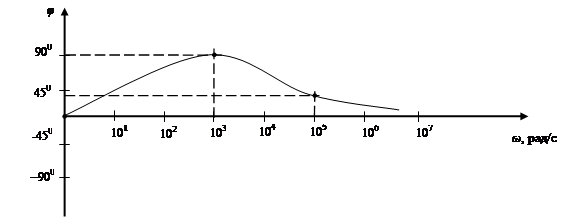
Рис. 3.8. Фазочастотная характеристика При этом на обоих графиках частота (а на первом – и модуль коэффициента передачи) отложена в логарифмическом масштабе. Очевидно, что при таком построении по нескольким точкам точность полученных характеристик является достаточно низкой и, кроме того, могут быть потеряны некоторые характерные точки.
Библиографический список
1. Попов В.П. Основы теории цепей: Учебник для вузов / В.П. Попов. – 5-е изд., стер.– М.: Высш. шк., 2005.
2. Бычков Ю.А. Основы теории электрических цепей: Учебник для вузов. 3-е изд., стер. / Ю.А. Бычков, В.М. Золотницкий, Э.П. Чернышев. СПб.: Издательство «Лань», 2004.
3. Иванов М.Г. Теоретические основы радиотехники: Учебн. пособие / М.Т. Иванов, А.Б. Сергиенко, В.Н. Ушаков; Под ред. В.Н. Ушакова. – М.: Высш. шк., 2002.
4. Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов по спец. «Радиотехника» / С.И. Баскаков. – 5-е изд., стер. – М.: Высш. шк., 2005.
5. Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач: Учебн. пособие для радиотехн. спец. вузов. – 2-е изд., перераб. и доп. – М.: Высш. шк., 2002
Раздел:
Коммуникации и связь Количество знаков с пробелами: 19909
Количество таблиц: 2
Количество изображений: 8
... по частям, как в пункте I}= II. В результате получаем закон изменения искомой величины при подаче на вход цепи импульса заданной формы: Расчет и построение графика спектральной плотности прямоугольного импульса Основой спектрального анализа является то, что любой непрерывный сигнал можно представить как периодический с периодом . Энергия ...
... цепи для передачи и преобразования электрической энергии и цепи для передачи и преобразования информации. Основные понятия и элементы линейных пассивных электрических цепей Электрический ток и напряжение - основные величины, характеризующие состояние электрических цепей. Электрический ток в проводнике есть упорядоченное перемещение электрических зарядов. Ток оценивают интенсивностью или ...
... , являющиеся произвольными функциями времени. К случайным воздействиям относятся различные виды помех от действия источников внутренних шумов в электронных приборах, резисторах и других элементах электрических цепей. Гармонические воздействия являются основным видом возмущений и реакций в энергетических сетях и системах. Генерирование гармонических напряжений и токов в диапазоне частот 10 ÷ ...
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...
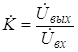 , (1.1)
, (1.1)![]() и
и ![]() - комплексные амплитуды выходного и входного напряжений;
- комплексные амплитуды выходного и входного напряжений;

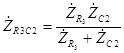 , (3.1) где комплексное сопротивление
, (3.1) где комплексное сопротивление 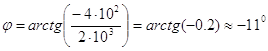 . (3.5) Поэтому комплексное сопротивление участка R3C2 можно записать, как
. (3.5) Поэтому комплексное сопротивление участка R3C2 можно записать, как 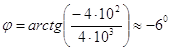 . (3.9) Поэтому комплексное сопротивление участка цепи можно записать, как
. (3.9) Поэтому комплексное сопротивление участка цепи можно записать, как 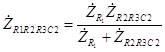 , (3.10) Комплексное сопротивление
, (3.10) Комплексное сопротивление 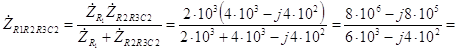
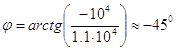 . (3.17) Поэтому полное комплексное сопротивление всей цепи можно записать как
. (3.17) Поэтому полное комплексное сопротивление всей цепи можно записать как 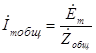 . (3.19) Комплексная амплитуда э.д.с. в общем виде в показательной форме может быть записана как
. (3.19) Комплексная амплитуда э.д.с. в общем виде в показательной форме может быть записана как 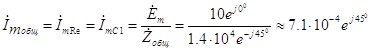 А . (3.20) Напряжение на сопротивлении Re равно произведению комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е.
А . (3.20) Напряжение на сопротивлении Re равно произведению комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е.



![]() . Для этого повторяются все расчеты (3.1) – (3.33) не подставляя в формулы числовое выражение частоты ω. В результате этого поучится выражение, содержащее зависимость от частоты;
. Для этого повторяются все расчеты (3.1) – (3.33) не подставляя в формулы числовое выражение частоты ω. В результате этого поучится выражение, содержащее зависимость от частоты; 
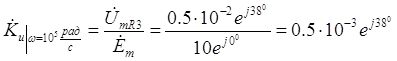 . (3.43) Рассмотрим еще одну точку частотной характеристики, например, соответствующую частоте ω = 103 рад/с. Для этого повторим расчеты (3.1) – (3.33) при новом значении частоты. Комплексное сопротивление
. (3.43) Рассмотрим еще одну точку частотной характеристики, например, соответствующую частоте ω = 103 рад/с. Для этого повторим расчеты (3.1) – (3.33) при новом значении частоты. Комплексное сопротивление 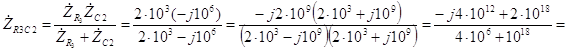
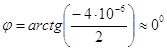 . (3.47) Поэтому искомое комплексное сопротивление участка цепи можно записать, как
. (3.47) Поэтому искомое комплексное сопротивление участка цепи можно записать, как 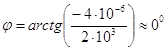 . (3.51) Поэтому искомое комплексное сопротивление участка цепи можно записать, как
. (3.51) Поэтому искомое комплексное сопротивление участка цепи можно записать, как 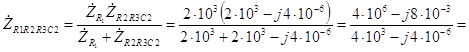
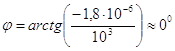 . (3.54) Поэтому искомое комплексное сопротивление участка цепи R1R2R3C2 можно записать, как
. (3.54) Поэтому искомое комплексное сопротивление участка цепи R1R2R3C2 можно записать, как 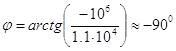 . (3.57) Поэтому полное комплексное сопротивление всей цепи можно записать как
. (3.57) Поэтому полное комплексное сопротивление всей цепи можно записать как 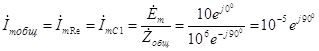 А. (3.58) Для участка цепи напряжение на сопротивлении Re может быть рассчитано как произведение комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е.
А. (3.58) Для участка цепи напряжение на сопротивлении Re может быть рассчитано как произведение комплексной амплитуды протекающего через него тока на комплексное сопротивление этого элемента, т.е.
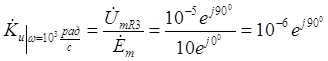 . (3.67) На рис. 3.7 и рис. 3.8 представлены графики амплитудно- и фазочастотных характеристик рассматриваемой схемы, полученные аналитическим путем.
. (3.67) На рис. 3.7 и рис. 3.8 представлены графики амплитудно- и фазочастотных характеристик рассматриваемой схемы, полученные аналитическим путем.


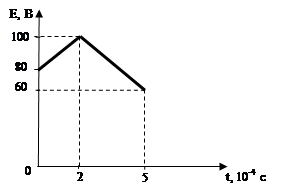

0 комментариев