ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ

2. ПРИМЕНЕНИЕ УРАВНЕНИЯ БЕРНУЛЛИ

Основными уравнениями, позволяющими решать простейшие задачи о движении идеальной жидкости,являеться уравнение расхода и уравнение Бернулли.

Уравнение расхода основано на условии неразрывности потока жидкости и представляет собой равенство объемных расходов во всех сечениях потока

Q₁ =Q₂ или V₁ S₁ = V₂ S₂ (2.1)

где Q₁ и Q₂ – расходы в сечении потока площадью S_{1 ,} S₂ ; V_{1 ,} V₂ -скорости потока жидкости в этих сечениях.

Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока. Уравнение Бернулли, отнесенное к еденице веса и записанное для сечения 1, 2, имеет вид:

 

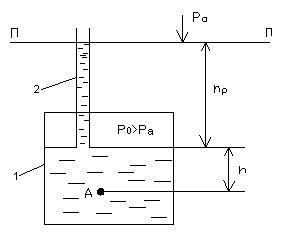
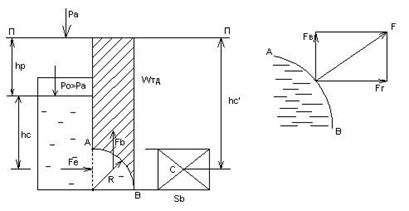
где Z – вертикальные координаты центров тяжести сечений; P/ρg - пневмотическая высота (напор) ; V²/2g - скоростная высота (напор); H – полный напор.

 

Задача 2.1

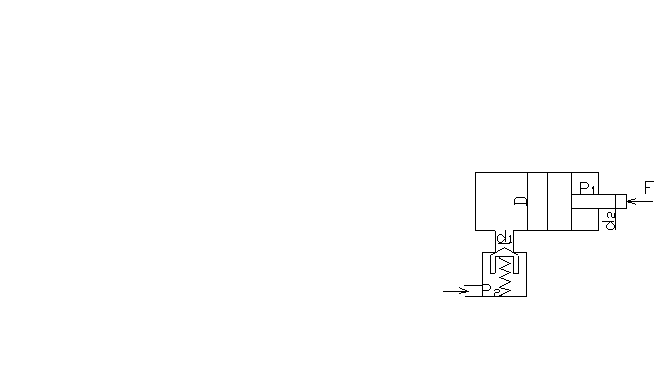
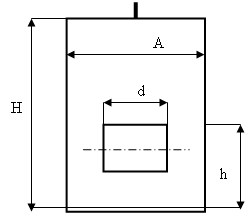
Из напорного бака вода течет по трубе диаметром d₁ = 0,02 м и затем вытекает в атмосферу через насадок с диаметром выходного отеврстия d₂ = 0,01 м. Избыточное давление воздуха в баке P₀ = 0,2МПа; высота H = 1,6 м. Пренебрегая потерями энергии определить скорость течения жидкости (воды) в трубопроводе V₁ и на выходе из насадки V_2.

Задача 2.2

Определить расход керосина, вытекающего из бака по трубопроводу диаметром d = 0,05 м, если избыточное давление воздуха в баке P₀ = 16кПа; высота уровня H₀ = 1 м; высота подъема керосина в пьезометре, открытом в атмосферу, H= 1,75 м. Потерями энергии принебречь. Плотность керосина ρ = 800 кг/ м³.

 

Задача 2.3

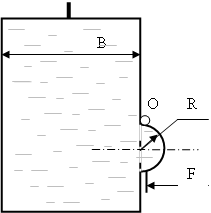
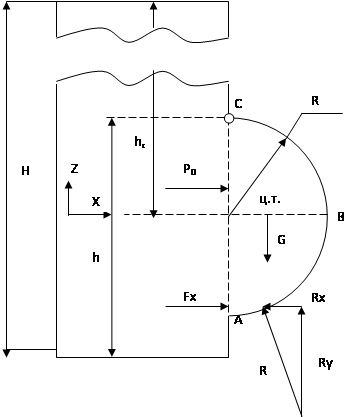
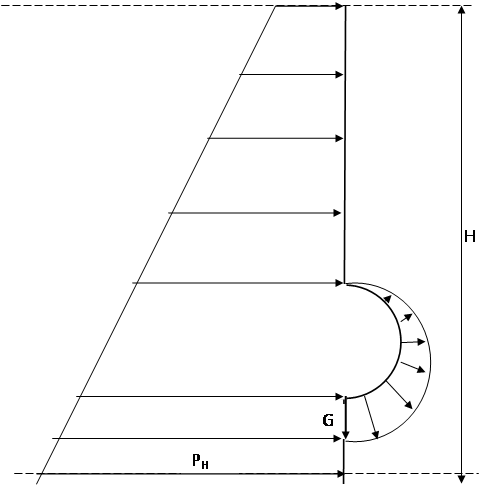
Жидкость вытекает из открытого резервуара в атмосферу через трубу, имеющую главное сужение до диаетра d_1. Истечение происходит под действием напора H= 3 м. Пренебрегая потерями энергии, определить абсолютное давление в узком сечении трубы 1-1, если соотношение соответсвует h₀ = 750 мм рт. ст. , плотность жидкости ρ = 1000 кг/ м³ . Найти напор H_кр, при котором абсолютное давление в сечении 1-1 будет равно нулю.

Указание: 1 мм рт. ст. – 133,3 Па. Уравнение Бернулли следует записать два раза, например, для сечения 0-0 и 2-2, а затем для сечения 1-1 и 2-2.

 

Задача 2.4

По длинной трубе диаметром d = 0,05 м протекает жидкость (ν = 2*10^-4 м²/с; ρ = 900 кг/ м³ ). Определить расход жидкости и давление в сечении, где установлен пьезометр (h=0,6 м) и трубка П то (H= 0,8 м).

 

Задача 2.5

Вода течет по трубе диаметром D = 0,02 м, имеющей отвеод (d = 0,008 м). Пренебрегая потерями напора, определить расход жидкости в отводе Q₁, если расход в основной трубе Q = 1,2*10^-3 м³/с; высоты H = 2 м, h = 0,5 м. Режим течения указать турбулентным, ρ = 1000 кг/ м³.

Указание: считать, что давление перед отводом расходится на создание скоростного напора в отводе и подъем жидкости на высоту.

3.               ГИДРАВЛИЧЕСКИЕ ПОТЕРИ.

Различают два вида гидравлических потерь: местные потери и потери на трение по длине. Местные потери напора происходят в так называемых гидравлических сопротивлениях, т.е. в местных изменениях формы и размеров русла. Местны потери выражаются формулой Вейсбаха

h_м = ξ_м ^. (3.1)

где V – средняя скорость потока в сечении перед местным сопротивлением или за ним; ξ_М = безразмерный коэффициент местного сопративления.

Числовое значение коэффициента ξ_М в основном определяется формой метсного сопративления, но иногда влияет число Рейнольдса, которое для труб диаметром d выражается формулой

R_e = = (3.2)

где ν - кинематическая вязкость жидкости (м²/с).

При R_e < R_{е кр,} где R_{е кр} ≈ 2300 – режим движения ламинарный.

При R_e > R_{е кр} – режим течения турбулентный.

Потери наопра на трение по длине l определяется ощей формулой Дарси

h_пр = λ ^. V²/2g (3.3)

где λ – безразмерный коэффициент на трение по длине и определяется в зависимости от режима течения:

при ламинарном режиме λ_л однозначно определяется число Рейнольдса, т.е.

λ_л = (3.4)

Потери давления от местных сопротивлений определяются выражением

ΔP=ρg h_м

(3.5)

ΔP= ξ_м ρ (3.6)

Если режим течения ламинарный, то потери давления по длине трубопровода считают по формуле Пуваейлля

ΔP= ν ρ Q (3.6)

где ν – кинематическая вязкость жидкости; ρ – плотность жидкости; Q – расход жидкости через сечение трубопровода диаметром d.

Если режим течения турбулентный, то потери давления по дилне трубопроода считают по формуле Дарон-Вейсбаха

ΔP= λ ρ

Для гидравлических гладких труб

λ=0,315^.R_e^-0,2

 

Задача 3.1

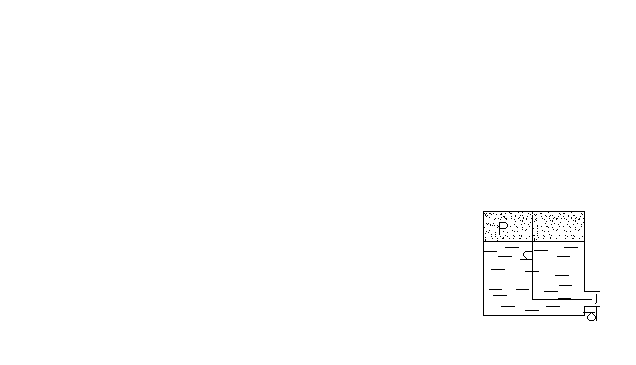
Определить потери давления в трубопроводе, если известно, что давление на его входе P = 0,4 МПа и коэффициент местных потерь ξ₁ = 0,5;

ξ₂ = 4,24; ξ₃ = 0,2; ξ₄ = 1,5. Плотность жидкости ρ = 900 кг/ м³ . Средняя скорость жидкости во всех сечениях трубопровода принять равной V = 2 м/с. Потерями на трение по длине пренебречь.

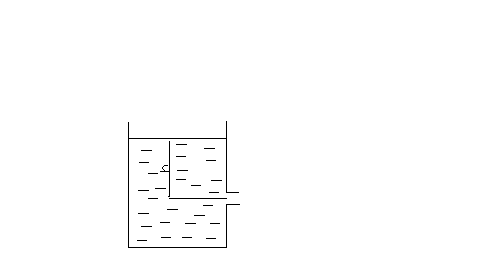
Задача 3.2

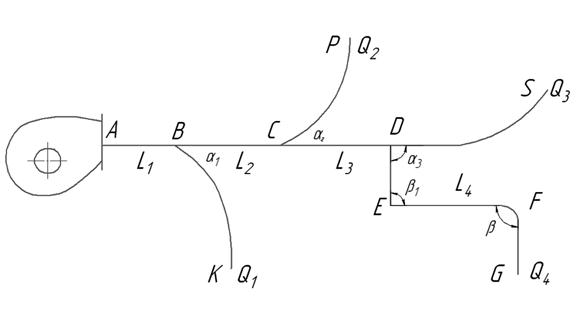
Определить потери давления на участке трубопровода, представленного на рис. 3.2, если известна скорость движения потока жидкости V = 3 м/с и плотность жидкости ρ = 1000 кг/ м³ . Коэффициенты местных поетрь ξ₁ = 6; ξ₂ = 1,2; ξ₃ = 1,7; ξ₄ = 0,8. ξ₅ = 6. Потерями на трение по длине пренебречь.

 

Задача 3.3

Определить давление на выходе трубопровода длиной l = 3м и диаметром d = 0,03 м, если расход трубопровода Q = 1,5 *10 ^-3 м³/с, коэффициент кинематической вязкости жидкости ν= 3* 10^-5 м²/с. Давление на входе трубопровода P = 0,4 МПа, ρ = 1000 кг/ м³ .

 

Задача 3.4

Рпеделить потери давления в трубопроводе длиной l = 5м и диаметром d = 0,01 м, если расход трубопровода Q = 4 *10 ^-3 м³/с, коэффициент кинематической вязкости жидкости ν= 3,6* 10^-5 м²/с.

 

Задача 3.5

 

Трубопровод длиной l = 4 м и диаметром d = 0,05 м имеет расход Q = 1 *10 ^-3 м³/с, коэффициент кинематической вязкости жидкости

ν= 3* 10^-5 м²/с. Давление на входе трубопровода P = 0,5 МПа. В конце участка трубопровода установлен патрубок с местными сопративлениями. Коэффициенты местных потерь ξ₁ = 0,5; ξ₂ = 0,8; ξ₃ = 1,2; ρ = 800 кг/ м³ . Определить потери давления.