Навигация
КОНКРЕТНІ ПРИКЛАДИ ВИЗНАЧЕННЯ РЕОЛОГІЧНИХ ХАРАКТЕРИСТИК
5. КОНКРЕТНІ ПРИКЛАДИ ВИЗНАЧЕННЯ РЕОЛОГІЧНИХ ХАРАКТЕРИСТИК
Для апроксимації експериментальних даних аналітичною залежністю, як правило, використовують метод найменших квадратів. Розглянемо цей метод на прикладі апроксимації реологічною кривою. Нехай для ряду значень ![]() отримано шляхом вимірювань ряд значень
отримано шляхом вимірювань ряд значень ![]()
![]() . Припустимо, що залежність
. Припустимо, що залежність ![]() від
від ![]() виражається лінійною функцією
виражається лінійною функцією ![]() , і знайдемо такі значення
, і знайдемо такі значення ![]() і
і ![]() , щоб сума квадратів відхилень від вибраної функції в експериментальних точках була мінімальна.
, щоб сума квадратів відхилень від вибраної функції в експериментальних точках була мінімальна.
Позначимо середньоквадратичне відхилення
![]() (42)
(42)
і знайдемо min![]() , розглядаючи
, розглядаючи ![]() як функцію
як функцію ![]() і
і ![]() . Це приводить до системи рівнянь
. Це приводить до системи рівнянь
![]() ;
; ![]() . (43)
. (43)
Підставляючи в цю систему вираз для ![]() і розв’язуючи стосовно
і розв’язуючи стосовно ![]() і
і ![]() , отримуємо:
, отримуємо:
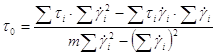 ; (44)
; (44)
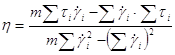 .
.
Для апроксимації експериментальних даних степеневої функції зручно застосовувати наступний підхід. Логарифмуючи залежність ![]() , отримуємо
, отримуємо
![]()
або (45)
T = k1 + nГ,
де Т = ![]() ;
; ![]() ; Г =
; Г = ![]() .
.
Якщо маємо ![]() виміряних значень
виміряних значень ![]() і
і ![]() , то можна записати
, то можна записати
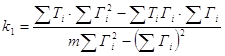 ; (46)
; (46)
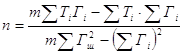 ;
;
![]() .
.
Приклад 1
Знайти реологічну криву ![]() розчину за наступними даними, які отримані на ротаційному віскозиметрі (
розчину за наступними даними, які отримані на ротаційному віскозиметрі (![]() =0.9).
=0.9).
Таблиця 1- Вихідні дані для розрахунку
| | 1 | 2 | 4 | 8 |
| | 5.5 | 9.5 | 18 | 28 |
Розв'язання
Згідно із (3) і (4) маємо
![]() ;
;
![]() .
.
Підставляючи показання віскозиметра, отримуємо значення , що наведені в табл. 2.
Таблиця 2 - Результати розрахунку ![]() і
і ![]()
|
| 9.53 | 19.06 | 38.12 | 76.24 |
|
| 4.98 | 8.6 | 16.29 | 25.34 |
Ці дослідні дані показані точками на рис. 5. Апроксимуємо експериментальні дані спочатку лінійною залежністю ![]() і знайдемо
і знайдемо ![]() і
і ![]() за допомогою методу найменших квадратів. Для цього попередньо підрахуємо такі суми:
за допомогою методу найменших квадратів. Для цього попередньо підрахуємо такі суми:
![]() 9.53 + 19.06 + 38.12 + 76.24 = 142.95,
9.53 + 19.06 + 38.12 + 76.24 = 142.95,
![]() = 4.98 + 8.6 + 16.29 + 25.34 = 55.21,
= 4.98 + 8.6 + 16.29 + 25.34 = 55.21,
![]() =4.98·9.53+8.6·19.06+16.29·38.12+25.34·76.24 =2764.27,
=4.98·9.53+8.6·19.06+16.29·38.12+25.34·76.24 =2764.27,
![]() = 9.532 + 19.062 + 38.122 + 76.242 = 7719.78.
= 9.532 + 19.062 + 38.122 + 76.242 = 7719.78.
За формулами (44) знаходимо:
![]()
![]()
![]() Па·с,
Па·с,
![]() Па.
Па.
Таким чином,
![]() (47)
(47)
Результати розрахунку за формулою (47) наведені в табл. 3, а графічне зображення - прямою 1 на рис. 5.
Таблиця 3 – Результати розрахунку за формулою (47)
|
| 9.53 | 19.06 | 38.12 | 76.24 |
|
| 5.83 | 8.69 | 14.41 | 25.84 |
Визначимо середньоквадратичне відхилення
![]() = (4.98 – 5.83)2 + (8.6 – 8.69)2 + (16.29 –
= (4.98 – 5.83)2 + (8.6 – 8.69)2 + (16.29 –
-14.41)2 + (25.34 – 25.84)2 = 4.52.
Аппроксимуємо експериментальні дані степеневою залежністю![]() . Результати розрахунку
. Результати розрахунку ![]() і
і ![]() наведені в табл. 4.
наведені в табл. 4.
Таблиця 4- Значення параметрів ![]() і
і ![]()
|
| 0.77 | 0.94 | 1.16 | 1.41 |
|
| 0.98 | 1.28 | 1.58 | 1.88 |
Визначимо такі суми:
![]() = 0.77 + 0.94 + 1.16 + 1.41 = 4.28,
= 0.77 + 0.94 + 1.16 + 1.41 = 4.28,
![]() = 0.98 + 1.28 + 1.58 + 1.88 = 5.72,
= 0.98 + 1.28 + 1.58 + 1.88 = 5.72,
![]() = 0.982 + 1.282 + 1.582 + 1.882 = 8.63,
= 0.982 + 1.282 + 1.582 + 1.882 = 8.63,
![]() = 0.77·0.98 + 0.94·1.28 + 1.16·1.58 + 1.41·1.88 =6.44.
= 0.77·0.98 + 0.94·1.28 + 1.16·1.58 + 1.41·1.88 =6.44.
За формулами (46) знаходимо:
![]() ,
,
![]() ,
,
![]() .
.
Таким чином,
![]() . (48)
. (48)
Результати розрахунку за формулою (48) наведені в табл. 5, а графічне зображення - кривою 2 на рис. 5.
Таблиця 5 – Результати розрахунку за формулою (48)
|
| 9.53 | 19.06 | 38.12 | 76.24 |
|
| 5.63 | 9.21 | 15.07 | 24.65 |
Визначимо середньоквадратичне відхилення
![]() = (4.98 - 5.63)2 + (8.6 – 9.21)2
= (4.98 - 5.63)2 + (8.6 – 9.21)2![]() +
+
+ (16.3 – 15.084)2 + (25.3 – 24.65)2 = 2.76.

Таким чином, у розглядуваному випадку степенева залежність краще апроксимує експериментальні дані, ніж лінійна залежність.
Приклад 2
Визначити реологічну криву рідини за даними Q i ![]() , отриманими на капілярному віскозиметрі.
, отриманими на капілярному віскозиметрі.
Таблиця 6 – Вихідні дані для розрахунку
|
| 0.98 | 5.9 | 11.8 | 18.2 |
|
| 2.5 | 10.5 | 18.3 | 26 |
Розв'язання
Застосовуючи інтерполяційну формулу Лагранжа, знаходимо зв'язок між ![]() і
і ![]() :
:
![]() .
.
Підставляючи цей вираз в (16), знаходимо
![]() =
= ![]()
![]() .
.
Підставляючи у формулу дані віскозиметра, знаходимо ![]() . Результати розрахунку наведені в табл. 7.
. Результати розрахунку наведені в табл. 7.
Таблиця 7 - Розрахунок швидкості зсуву ![]()
|
| 2.5 | 10.5 | 18.3 | 26 |
|
| 4.24 | 24.83 | 49.15 | 73.91 |
Ці результати показані точками на рис. 6. Апроксимуємо дані табл. 7 спочатку лінійною залежністю ![]() і знайдемо
і знайдемо ![]() і
і ![]() за допомогою методу найменших квадратів. Для цього попередньо обчислюємо такі суми:
за допомогою методу найменших квадратів. Для цього попередньо обчислюємо такі суми:
![]() = 4.24 + 24.83 + 49.15 + 73.91 = 152.13,
= 4.24 + 24.83 + 49.15 + 73.91 = 152.13,
![]() = 2.5 + 10.5 + 18.3 + 26 = 57.3,
= 2.5 + 10.5 + 18.3 + 26 = 57.3,
![]() = 2.5·4.24 + 10.5·24.83 + 18.3·49.15 + 26·73.91=
= 2.5·4.24 + 10.5·24.83 + 18.3·49.15 + 26·73.91=
= 3092.42,
![]()
![]() = 4.242 + 24.832 + 49.152 + 73.912 = 8512.92.
= 4.242 + 24.832 + 49.152 + 73.912 = 8512.92.
За формулами (44) знаходимо
![]() Па,
Па,
![]() = 0.335 Па·с.
= 0.335 Па·с.
Таким чином
![]() . (49)
. (49)
Результати розрахунку за формулою (49) наведені в табл. 8, а графічне зображення - прямою 1 на рис. 6.
Таблиця 8 – Результати розрахунку за формулою (49)
|
| 4.24 | 24.83 | 49.15 | 73.91 |
|
| 3.01 | 9.91 | 18.06 | 26.35 |
Визначимо середньоквадратичне відхилення
![]() = (2.5 – 3.01)2 + (10.5 - 9.91)2 +
= (2.5 – 3.01)2 + (10.5 - 9.91)2 +
+ (18.3 – 18.06)2 + (26 – 26.35)2 = 0.778.
Апроксимуємо експериментальні дані степеневою залежністю![]() . Результати розрахунку
. Результати розрахунку ![]() і
і ![]() наведені в табл. 9.
наведені в табл. 9.
Таблиця 9 – Значення параметрів ![]() і
і ![]()
|
| 0.398 | 1.021 | 1.262 | 1.415 |
|
| 0.627 | 1.395 | 1.692 | 1.869 |
Визначимо такі суми:
![]() = 0.627 + 1.395 + 1.692 + 1.869 = 5.583,
= 0.627 + 1.395 + 1.692 + 1.869 = 5.583,
![]() = 0.398 + 1.021 + 1.262 + 1.415 = 4.096,
= 0.398 + 1.021 + 1.262 + 1.415 = 4.096,
![]() = 0.6272 + 1.3952 + 1.6922 + 1.8692 = 8.695,
= 0.6272 + 1.3952 + 1.6922 + 1.8692 = 8.695,
![]() = 0.398·0.627 + 1.021·1.395 +
= 0.398·0.627 + 1.021·1.395 +
+ 1.262·1.692 +1.415·1.869 = 6.454.
За формулами (46) знаходимо
![]() ,
,
![]() ,
,
![]() .
.
Таким чином
![]() (50)
(50)
Результати розрахунку за формулою (50) наведені в табл. 10, а графічне зображення - кривою 2 на рис. 6.
Таблиця 10 – Результати розрахунку за формулою (50)
|
| 4.24 | 24.83 | 49.15 | 73.91 |
|
| 2.49 | 10.57 | 18.46 | 25.76 |
Визначимо середньоквадратичне відхилення
![]() (2.5 – 2.49)2 + (10.5 – 10.57)2 +
(2.5 – 2.49)2 + (10.5 – 10.57)2 +
+ (18.3 – 18.46)2 + (26 – 25.76)2 = 0.088.

Таким чином, у розглядуваному випадку степенева залежність краще апроксимує експериментальні дані, ніж лінійна залежність.
Приклад 3
Визначити реологічну криву гірської породи, виходячи з даних дослідів на одноосне стиснення.
Таблиця 11 - Вихідні дані для розрахунку
|
| 1.2 | 4.1 | 13 | 25 |
|
| 1.8 | 2.5 | 3.5 | 5.2 |
Визначимо такі суми:
![]() (1.8 + 2.5 + 3.5 +5.2)·105 = 13·105,
(1.8 + 2.5 + 3.5 +5.2)·105 = 13·105,
![]() (1.2 + 4.1 + 13 + 25)·10-8 = 43.3·10-8,
(1.2 + 4.1 + 13 + 25)·10-8 = 43.3·10-8,
![]() (1.8·1.2 + 2.5·4.1 + 3.5·13 + 5.2·25)·10-3=
(1.8·1.2 + 2.5·4.1 + 3.5·13 + 5.2·25)·10-3=
=187.91·10-3,
![]() = (1.22 + 4.12 + 132 + 252) = 812.25·10-16.
= (1.22 + 4.12 + 132 + 252) = 812.25·10-16.
За формулами (44) знаходимо:
![]() ,
,
![]() .
.
Використовуючи формулу (36), маємо
![]() . (51)
. (51)
Тоді за (35):
![]()
![]() .
.
Таким чином отримали реологічне рівняння
![]() . (52)
. (52)
Результати розрахунку за формулою (51) наведені в табл. 11, а графічне зображення - прямою 1 на рис. 7.
Таблиця 11 – Результати розрахунку за формулою (51)
|
| 1.2 | 4.1 | 13 | 25 |
|
| 1.92 | 2.32 | 3.54 | 5.19 |
Визначимо середньоквадратичне відхилення
![]() (1.8 – 1.92)2 + (2.5 – 2.32)2 + (3.5 –
(1.8 – 1.92)2 + (2.5 – 2.32)2 + (3.5 –
-3.54)2 + (5.2 – 5.19)2 = 0.0485.
Апроксимуємо експериментальні дані степеневою залежністю (39). Результати розрахунку ![]() і
і ![]() наведені в табл. 12.
наведені в табл. 12.
Таблиця 12 – Значення параметрів ![]() і
і ![]()
|
| -7.921 | -7.387 | -6.886 | -6.602 |
|
| 5.255 | 5.3985 | 5.5441 | 5.716 |
Визначимо такі суми:
![]() = 5.255 + 5.3985 + 5.5441 + 5.716 = 21.9136,
= 5.255 + 5.3985 + 5.5441 + 5.716 = 21.9136,
![]() = -7.921 – 7.387 – 6.886 – 6.602 = -28.796,
= -7.921 – 7.387 – 6.886 – 6.602 = -28.796,
![]() = 7.9212 + 7.3872 + 6.8862 + 6.6022 = 208.313,
= 7.9212 + 7.3872 + 6.8862 + 6.6022 = 208.313,
![]() = -5.255 · 7.921 – 5.3985 · 7.387 – 5.5441 · 6.886 –
= -5.255 · 7.921 – 5.3985 · 7.387 – 5.5441 · 6.886 –
-5.716 · 6.602 = -157.417.
За формулами (46) знаходимо:
![]() ,
,
![]()
![]() ,
,
![]() .
.
Використовуючи формулу (39), маємо
![]() . (53)
. (53)
Результати розрахунку за формулою (53) наведені в табл. 13, а графічне зображення - кривою 2 на рис. 7.
Таблиця 13 – Результати розрахунку за формулою (53)
|
| 1.2 | 4.1 | 13 | 25 |
|
| 1.72 | 2.6 | 3.83 | 4.77 |
 |
Згідно з формулами (41) маємо:
![]() ,
,
![]() .
.
Реологічне рівняння (40) має вигляд
![]() . (54)
. (54)
Визначимо середньоквадратичне відхилення
![]() (1.8 – 1.72)2 + (2.5 – 2.6)2 + (3.5 – 3.83)2 +
(1.8 – 1.72)2 + (2.5 – 2.6)2 + (3.5 – 3.83)2 +
+(5.2 – 4.77)2 = 0.31.
У даному випадку модель в’язкопластичної рідини краще апроксимує реологію гірської породи, ніж модель степеневої рідини.
СПИСОК ЛІТЕРАТУРИ
1. Шищенко Р.И., Есьман Б.И., Кондратенко П.И. Гидравлика промывочных жидкостей. – М.: Недра, 1976.- 294 с.
2. Леонов Е.Г., Исаев В.И. Гидроаэромеханика в бурении.- М.: Недра, 1987. – 300 с.
3. Астарита Дж., Марручи Дж. Основы гидромеханики неньютоновских жидкостей. - М.: Мир, 1978.
Похожие работы
... збір матеріалу, його аналіз. Співавтор проф. Герасимчук Р. Д. відредагував висновки). АНОТАЦІЯ Дорошенко О.О. Клініко-генетичні співвідношення геморагічних інсультів та патогенетично-гемодинамічне обґрунтування лікувальної тактики при субарахноїдальних крововиливах. – Рукопис. Дисертація на здобуття наукового ступеня кандидата медичних наук за спеціальністю 14.01.15. – нервові хвороби. – ...
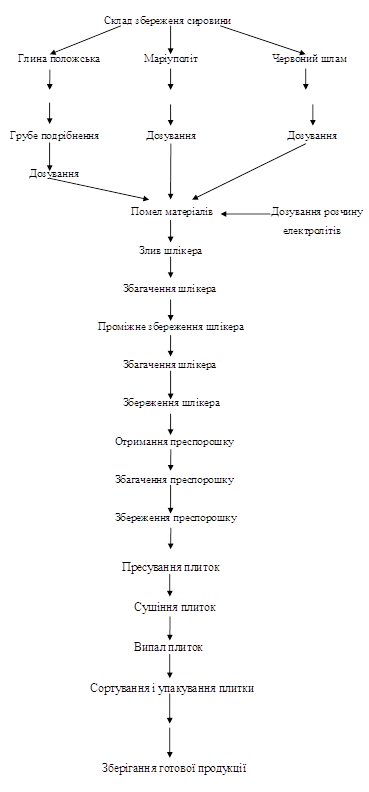
... ; 11 - канал конвеєра; 12 - відкрита частина конвеєра; 13,14,15 - вентилятори; 16 - теплообмінник Рисунок 2.6 - Потоково-конвеєрна лінія Буде встановлено 2 потоково-конвеєрних ліній для виробництва плиток для підлоги продуктивністю 400 тис м²/рік. 2.5.11 Розрахунок складу готової продукції При розрахунку складу готової продукції необхідно знати запас виробів, вид упаковки, площу, що ...
... орієнтовну величину основних параметрів цих машин, що є початковими при їх подальших розрахунках. Розділ 3. Дозування сипких і рідких матеріалів 3.1. Дозування будівельних матеріалів і рідких продуктів Сучасне виробництво будівельних матеріалів, виробів і конструкцій характеризується широким використовуванням багатокомпонентних будівельних сумішей. При їх приготуванні значна увага ві ...
... досліджень, участь в обстеженні хворих, аналіз та обробка результатів, написання тез. АНОТАЦІЯ Гуменюк М.І. Обґрунтування застосування інфузійних препаратів на основі сорбітолу та натрію лактату в комплексному лікуванні хворих із легеневою недостатністю та хронічним легеневим серцем. − Рукопис. Дисертація на здобуття наукового ступеня доктора медичних наук за спеціальністю 14.01.27. &# ...

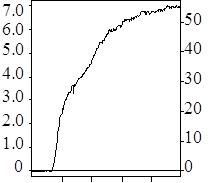
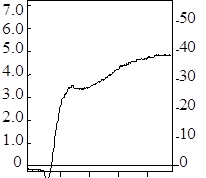
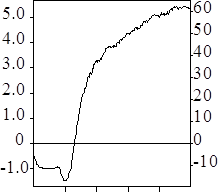
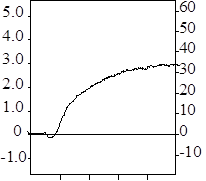
0 комментариев