Навигация
Магнітний потік. Теорема Гаусса для магнітного поля
2. Магнітний потік. Теорема Гаусса для магнітного поля
Потоком магнітної індукції або магнітним потоком називають скалярну величину, яка дорівнює:
![]() , (2.1)
, (2.1)
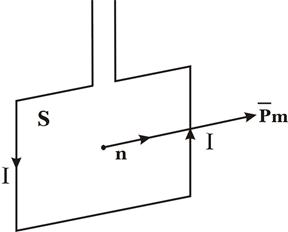
де ![]() - вектор індукції магнітного поля у напрямку нормалі до площадки dS (рис.13.3)
- вектор індукції магнітного поля у напрямку нормалі до площадки dS (рис.13.3)

Рис.13.3
Повний магнітний потік через поверхню S знаходять шляхом інтегрування.
Магнітному потоку в 1 Вб відповідає 108 силових ліній індукції магнітного поля крізь площадку в 1 м2.
У випадку замкнутої поверхні слід відрізняти між собою такі особливості:
- силові лінії, які входять у поверхню, мають від’ємний потік, тому в цьому випадку
![]()
- силові лінії, які виходять з поверхні мають
![]()
- у загальному випадку
![]() . (2.2)
. (2.2)
Вираз (2.2) є теоремою Гаусса для магнітного поля. Суть цієї теореми полягає в тому, що силові лінії магнітного поля не пов’язані з магнітними зарядами. Магнітних зарядів у природі не існує. Описане явище показане на рис. 4.
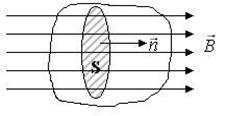
Рис.4
![]() . (2.3)
. (2.3)
3. Робота переміщення провідника із струмом і контуру із струмом у магнітному полі
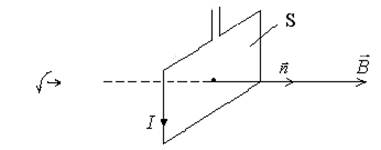
Знайдемо роботу, яку слід виконати для переміщення провідника із струмом І у магнітному полі, як це показано на рис. 13.5
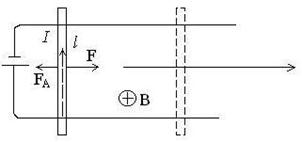
Рис.13.5
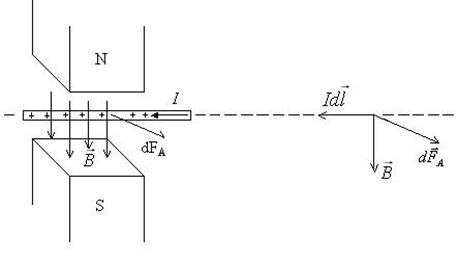
Провідник, що має довжину l і струм І виготовлений у вигляді коточка і має можливість переміщуватись. На рухому частину провідника з сторони магнітного поля діє сила Ампера, напрям якої визначається правилом лівої руки.
Для переміщення такого коточка вздовж направляючих дротів слід прикладати силу F, яка має бути рівною силі Ампера. Робота в цьому випадку буде дорівнювати:
![]() . (13.3.1)
. (13.3.1)
де FA=IBl – величина сили Ампера, яка діє на рухомий коточок, тому:
A = -Ibldx = -IbdS = -Id (3.2)
Знак мінус показує, що робота виконується проти сили Ампера.
Якщо роботу виконує сила Ампера, то
A= Id (3.3)
де А – позитивна робота, виконана силою Ампера.
Після інтегрування одержуємо роботу сили по переміщенню провідника із струмом у магнітному полі.
A = -I,
або
A =I. (3.4)
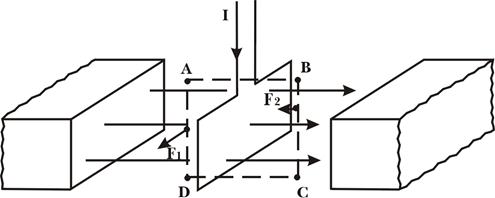
У випадку контуру із струмом, який рухається у магнітному полі, слід враховувати як позитивну роботу, так і негативну роботу переміщення двох частин цього контуру (рис.13.6)
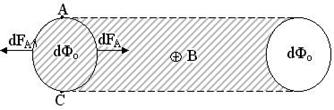
Рис.6
При русі частини контуру АС (зліва) робота виконується позитивна. Тому в цьому випадку
A1 = I(d1 + d0), (3.5)
де dФ1 – потік, який визначається площею лівої частини контуру АС (заштрихована площа),
dФ0 - потік, який визначається площею самого контуру з струмом.
При переміщенні правої сторони цього контуру робота буде дорівнювати
A2 = -I(d2 + d0), (3.6)
де dФ2 – потік, який утвориться переміщенням правої частини контуру; dФ0 – потік за рахунок площі самого контуру.
Ця площа перекривається площею правої сторони контуру. Робота А2 – від’ємна
У загальному випадку робота переміщення контуру з струмом у магнітному полі буде дорівнювати
A = I(d1 - d2)= Id. (3.7)
Після інтегрування одержимо
А=ІФ. (3.8)
Висновок. Робота переміщення провідника із струмом і контуру із струмом визначається однаковою формулою.
4. Енергія магнітного поля
Розглянемо замкнуте коло, в якому є резистор R, котушка L і джерело струму (рис.7)
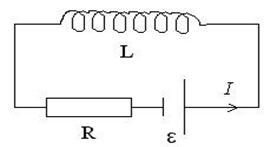
Рис.7
Скористаємось другим правилом Кірхгофа для замкнутого контуру, показаного на рис.7.
У цьому випадку
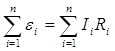 , (4.1)
, (4.1)
або
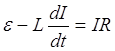 , (4.2)
, (4.2)
де ![]() - електрорушійна сила самоіндукції, діє лише в момент замикання або розмикання кола.
- електрорушійна сила самоіндукції, діє лише в момент замикання або розмикання кола.
З рівняння (13.4.2) визначимо електрорушійну силу джерела
![]() .
(4.3)
.
(4.3)
Зведемо цей вираз до спільного знаменника
dt = Irdt + LdI . (4.4)
Помножимо вираз (13.4.4) на струм І, одержимо
Idt = I2rdt + LIdI , (4.5)
де I2rdt - джоулевe тепло; Idt - робота сторонніх сил джерела струму; LIdI - енергія магнітного поля, локалізована в котушці зі струмом.
Тому
dWм= LIdI . (4.6)
Інтегруємо цей вираз у межах зміни енергії магнітного поля від 0 до Wм, а струму від 0 до І, одержимо
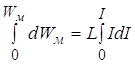 ,
,
або
![]() . (4.7)
. (4.7)
Вираз (13.4.7) визначає енергію магнітного поля котушки зі струмом.
Для довгого соленоїда L=0n2V. Підставимо це значення L у (13.4.7), одержимо
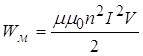 . (4.8)
. (4.8)
де 202n2І2=В2 – квадрат індукції магнітного поля соленоїда.
З урахуванням цього зауваження одержуємо:
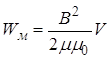 .
(4.9)
.
(4.9)
При діленні енергії магнітного поля на об’єм одержимо об’ємну густину енергії магнітного поля, локалізованого в котушці
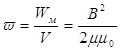 ,
,
або
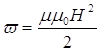 . (4.10)
. (4.10)
Похожие работы
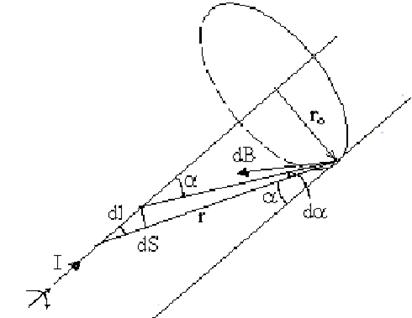
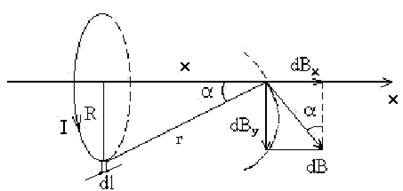
... тного поля в точці на осі колового провідника радіусом R на відстані d від центра колового провідника дорівнює: . Аналогічно обчислюється індукція магнітного поля, створена іншими провідниками з струмом. 2. ЗАКОН ПОВНОГО СТРУМУ ТА ЙОГО ВИКОРИСТАННЯ ДЛЯ РОЗРАХУНКУ МАГНІТНИХ ПОЛІВ. ВИХРОВИЙ ХАРАКТЕР МАГНІТНОГО ПОЛЯ У електростатиці було встановлено, що робота при переміщенні одиничного ...
... з струмом, лінійні розміри якого досить малі. Магнітне поле такого пробного контуру не повинно створювати зовнішнього магнітного поля. При розміщенні такої рамки у досліджуване зовнішнє магнітне поле, із сторони останнього, на рамку діятиме обертальний момент сил М. Елементарна рамка із струмом займе певний напрям у просторі так, щоб магнітне поле рамки і досліджуваного магнітного поля збігалися ( ...
... тне поле, хоча щодо доцільності такого підходу існують різні точки зору. Найчастіше людина має справу з полем частотою 50 Гц, яка прийнята як промислова частота (у США – 60 Гц). Щодо впливу на людину електромагнітного поля промислової частоти, саме електричне поле розглядається як таке, яке може становити небезпеку. Магнітне поле, проте, за даними останніх досліджень, також «під підозрою» - йому ...
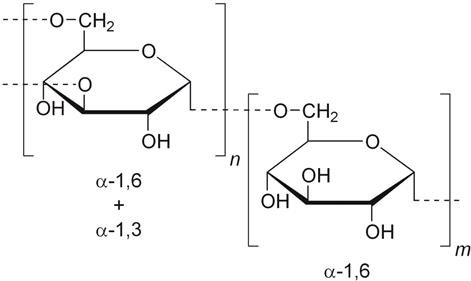
... у змішувач. Отримане поживне середовище передають на стерилізацію та охолодження. Культивування продуцентів (Leuconostoc mesenteroides PCSIR-4) здійснюють до утворення полісахариду необхідної в’язкості (18 год) [8, 28]. Крім етапів синтезу продукту і їх очистки, технологія виробництва декстрану містить етап фракціонування. Фракціонування декстранів на виробництві проводять з використанням спирт ...
0 комментариев