Физико–математическое моделирование процессов высокотемпературного окисления вольфрамовой проволочки с учетом испарения оксидной пленки

2.2. Физико–математическое моделирование процессов высокотемпературного окисления вольфрамовой проволочки с учетом испарения оксидной пленки.

 

Рассмотрим нестационарный тепломассообмен (ТМО) и кинетику окисления вольфрамового проводника, нагреваемого электрическим током, в воздухе при комнатной температуре. Выделяемое при этом джоулево тепло приводит к увеличению температуры проводника и к активизации на его поверхности химической реакции окисления металла

Как было отмечено в главе 1, при окислении вольфрама в воздухе возможно образование двух устойчивых окислов WO₂ и WO₃ согласно уравнениям:

W+O₂®WO₂ (I)

2W+3O₂®2WO₃ (II).

Предположим, что на поверхности проволочки образуется окисная пленка, состоящая только из WO₂ . Так как реакция окисления протекает по параболическому закону, то скорость химической реакции по кислороду лимитируется толщиной оксидной пленки

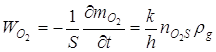, , (2.3)

где k – константа скорости химической реакции, ; h – толщина оксидной пленки, м; относительная массовая концентрация кислорода на поверхности металла; r_g – плотность воздуха, ; скорость окисления по кислороду, ; k₀ – предэкспоненциальный множитель, ; Е – энергия активации, .

Концентрацию кислорода на поверхности проволоки  найдем из условия равенства массового потока кислорода к поверхности и скорости его потребления на границе металл – окисел [2]:

,

,

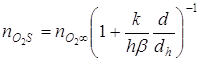 , (2.4)

где S_h,d_h,S, d – соответственно площадь поверхности и диаметр проводника, покрытого слоем окисла толщиной h, и чистого металлического проводника без оксидного покрытия. Для тонких оксидных пленок, наблюдаемых при окислении вольфрама, можно считать, что d_h/d»1 (d_h =d+2h).

Это дает нам возможность определить плотность химического тепловыделения реакции окисления вольфрама в виде:

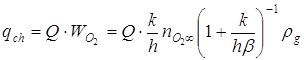. (2.5)

В уравнениях (2.4), (2.5) : относительная массовая концентрация кислорода в воздухе, =0.23 при Р_атм=10⁵Па; Q – тепловой эффект реакции, ; коэффициент массообмена, , который определяется условиями массообмена проволочки с воздухом и характерным ее размером:

, (2.6)

где Sh – критерий Шервуда; D – коэффициент диффузии кислорода в воздухе, ; d – диаметр проволоки, м.

Молекулярно–конвективный теплообмен нагретой проволочки с воздухом описывается законом Ньютона–Рихмана:

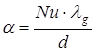, ,  (2.7) где q_c–плотность теплового потока молекулярно–конвективным путем, ; T_g – температура газа, К; коэффициент теплообмена, ; коэффициент теплопроводности газа, ; Nu – критерий Нуссельта.

Для тонких проволочек можно принять, что Nu = Sh=0.5 [12]

Для проволочек в поперечном потоке воздуха в интервале чисел Рейнольдса:

1<Re<4 для Nu можно пользоваться зависимостью.

, ,

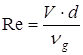V – скорость потока, ;  коэффициент кинематической вязкости воздуха, .

В области 4<Re<40 используется зависимость:

Для областей 40<Re<10³ рекомендуется зависимость

Nu_f=0.52Re^0.5_f Pr^0.37_f(Pr_f /Pr_w)^0.25,

Pr – критерий Прандтля, индекс ²w² – свойства рассчитаны у стенки, т.е. при температуре проволочки, ²f ² при температуре набегающего газа.

Нагреваемая проволочка теряет часть энергии в результате лучистого теплообмена со стенками реакционной установки, который описывается законами Кирхгофа и Стефана–Больцмана:

, (2.8)

где q_r– плотность теплового потока излучением, ; степень черноты оксидной пленки; постоянная Стефана – Больцмана, ; T_w температура стенок реакционной установки, К. В нашем случае T_w= T_g= T_k, где T_k – комнатная температура воздуха, К.

В местах контакта вольфрамовой проволочки с токоподводящими проводами возникает тепловой поток теплопроводностью, направленный к соединительным проводам и приводящий к понижению температуры проволочки. Как было сказано в главе 2, теплопотери проволочки через ее концы определяется выражением :

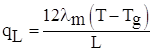, (2.9)

q_L – плотность теплового потока теплопроводностью, .

Считаем, что температура подводящих проводов равна температуре окружающего воздуха T_g.

Мощность электрического тока, нагревающего проводник, с учетом зависимостей от геометрических размеров и температуры, представим в виде:

.  (2.10)

Как было изложено в главах 1 и 2, окислы вольфрама летучи и при достижении определенных температур происходит их возгонка и испарение.

Интенсивное испарение окисла WO₂ начинается после его плавления, которое происходит при температуре, лежащей в интервале 1500–1600 К. Учтем в тепловом балансе проводника теплопотери, идущие на испарение окисла WO_2.

Плотность теплового потока, затрачиваемая на испарение окисла, зависит от удельной теплоты испарения  и скорости испарения:

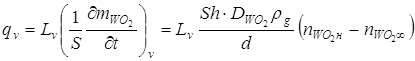, (2.11)

где  коэффициент диффузии окисла WO₂ в воздухе, ;

, относительная массовая концентрация паров WO₂ в насыщенном состоянии на поверхности частицы и на бесконечном удалении от нее.

Используя для паров WO₂ приближение идеального газа, найдем :

,

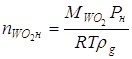молярная масса WO_2.

Давление насыщенных паров зависит от температуры по закону Клапейрона–Клаузиуса:

,

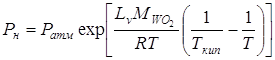где Т_кип – температура кипения WO₂ при атмосферном давлении .

С учетом выше изложенного, (2.23) преобразуется к виду:

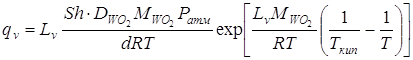. (2.12)

В предположении Вi<0 запишем дифференциальное уравнение для изменения температуры проводника с учетом описанных выше физических и химических процессов, протекающих на его поверхности:

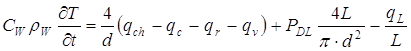, Т(t=0)=T₀, (2.13)

где удельная теплоемкость и плотность вольфрама, ; ;

Т₀ – начальная температура проводника, К.

Изменение толщины оксидной пленки со временем происходит в результате реакции окисления вольфрама и испарения окисла с поверхности:

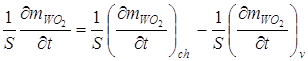. (2.14)

Для тонких пленок считаем, что S_h»S. Так как:

 ,

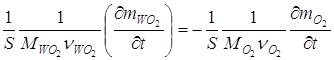то ; ,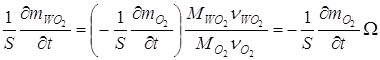

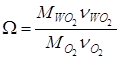где Мо₂ – молярная масса О₂ ;  стехиометрические коэффициенты в реакции окисления W+O₂®WO₂, .

Тогда с учетом (2.3) для скорости образования окисла имеем:

.

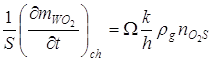Используя (2.10) и учитывая, что 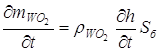,S_б=pdL, из (2.14) определим временную зависимость толщины оксидной пленки на поверхности проводника:

,

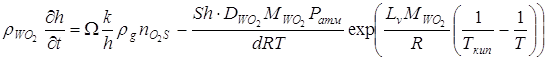 . (2.15)

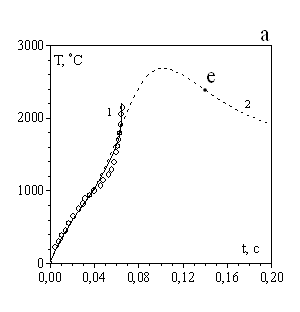
Дифференциальные уравнения (2.13), (2.14) с учетом уравнений (2.9), (2.5)–(2.12) описывают нестационарный высокотемпературный тепломассообмен и кинетику окисления вольфрамового проводника, нагреваемого электрическим током в газообразной среде, с учетом испарения окисла с его поверхности. На рис.2.3 представлены зависимости T(t) и h(t), рассчитанные по указанным формулам для вольфрамового проводника, нагреваемого электрическим током в среде кислорода. Результаты представлены в сравнении с экспериментальными данными А. Г. Мержанова [10]. Кривая 2 описывает зависимости T(t) и h(t) без учета теплопотерь на испарение. Высокотемпературное состояние характеризуется максимальным значением температуры, которая затем уменьшается по мере роста толщины оксидного слоя. При достижении толщиной окисла критического значения h_E происходит затухание реакции окисления на поверхности проводника, вследствие уменьшения плотности химического выделения. С учетом испарения оксида с поверхности проводника толщина оксидной пленки увеличивается (кривая 1), достигает максимального значения, а затем убывает, т.к. скорость испарения ее при высоких температурах больше скорости образования окисла. Результаты расчетов по физико–математической модели с учетом испарения хорошо согласуются с экспериментальными данными. С уменьшением мощности электрического тока, нагревающего проводник, увеличивается время высокотемпературного окисления проводника и максимальное значение толщины оксидной пленки, т.к. при более низких температурах скорость испарения окисла меньше.

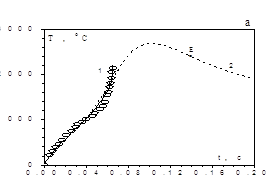
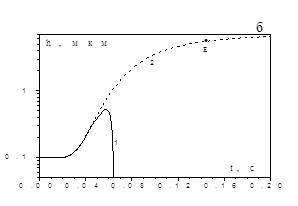
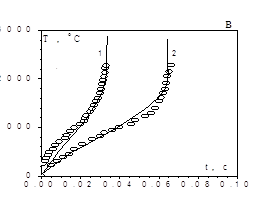
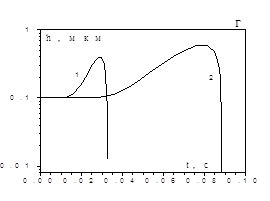
Рис.2.3. Временные зависимости температуры вольфрамового проводника и толщины окисла на его поверхности. d=50 мкм, L=7 см, =1, v=0.13 м/с.

а), б): 1-q_v¹0, 2-q_v=0, Р=106,4 Вт/см²;

в), г): q_v¹0, 1-Р=194.4 Вт/см², 2-Р=91.3 Вт/см²;

^ооо - экспериментальные данные [10]; Р –постоянная мощность нагрева электрическим током; υ – скорость обдува проводника.

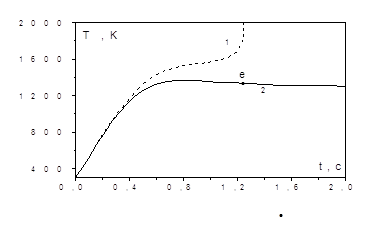
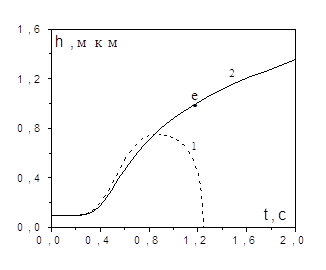
Рис. 2.4. Влияние теплообмена излучением на временные зависимости температуры и толщину оксидной пленки вольфрамового проводника.

l = 10 см , d = 10 мкм ; T_g=288 K , .

1- q=0, 2 - q,

T_w= 288 K