Алгебраическое доказательство теоремы Пифагора

Алгебраическое доказательство теоремы пифагора

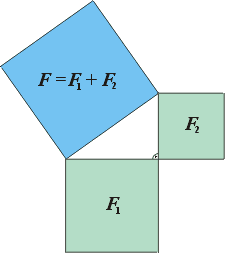
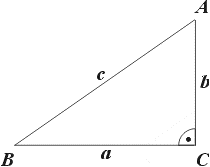
Теорема Пифагора формулируется следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

С²=А² + В², /1/

где: С - гипотенуза;

А и В - катеты.

Существуют прямоугольные треугольники, у которых стороны А, В и С выражаются целыми числами. Такие числа называются пифагоровыми.

Рассматривая уравнение теоремы Пифагора как алгебраическое уравнение, докажем, что существует бесконечное количество прямоугольных треугольников, в которых их стороны выражаются целыми числами или, что одно и тоже, уравнение /1/ имеет бесконечное количество решений в целых числах.

Суть теоремы Пифагора не изменится, если уравнение /1/ запишем следующим образом:

А² = С² -В² /2/

Для доказательства теоремы Пифагора методами элементарной алгебры используем два известные в математике метода решения алгебраических уравнений: метод решения параметрических уравнений и метод замены переменных.

Уравнение /2/ рассматриваем как параметрическое уравнение с параметром A и переменными B и С. Уравнение /2/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:

А²= (C-B) (C+B) /3/

Используя метод замены переменных, обозначим:

C-B=M /4/

Из уравнения /4/ имеем:

C=B+M /5/

Из уравнений /3/, /4/ и /5/ имеем:

А² =M∙ (B+M+B) =M∙ (2B+M) = 2BM+M² /6/

Из уравнения /6/ имеем:

А² - M²=2BM /7/

Отсюда: B = /8/

Из уравнений /5/ и /8/ имеем:

C= 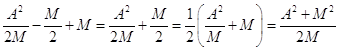 /9/

Таким образом:

B = /10/

C  /11/

Из уравнений /8/ и /9/ следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа A² на число M, т.е. число M должно быть одним из множителей, входящих в состав множителей числа А или A².

Числа А и M должны иметь одинаковую четность.

По формулам /10/ и /11/ определяются числа B и C как переменные, зависящие от значения числа А как параметра и значения числа M.

Из изложенного следует:

Квадрат простого числа A равен разности квадратов одной пары чисел B и C (при M=1).

Квадрат составного числа A равен разности квадратов одной пары или нескольких пар чисел B и C.

Все числа являются пифагоровыми.

Таким образом, существует бесконечное количество троек пифагоровых чисел А, В и С и, следовательно, бесконечное количество прямоугольных треугольников, у которых стороны А, В и С выражаются целыми числами.