ДОКАЗАТЕЛЬСТВО ГИПОТЕЗЫ БИЛЯ
Файл: HIPOTESA
© Н.М. Козий, 2007
Авторские права защищены свидетельствами
Украины № 23145, №27312 и № 28607
Доказательство гипотезы биля
Гипотеза Биля формулируется следующим образом: неопределенное уравнение (http: // soluvel. okis. ru/vertex. html):
Аx + Вy = Сz /1/
не имеет решения в целых положительных, т.е. натуральных числах A, B, C, x, y и z при условии, что x, y и z больше 2.
Суть гипотезы Биля не изменится, если уравнение /1/ запишем следующим образом:
Аx = Сz -Вy /2/
Обозначим: Вy =V2 /3/
Сz =U2 /4/
Тогда: В =![]() /5/
/5/
С =![]() /6/
/6/
Из уравнений /2/, /3/ и /4/ следует:
Аx = Сz -Вy =U2-V2 /7/
Уравнение /7/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:
Аx=(U-V) ∙(U+V) /8/
Для доказательства великой теоремы Ферма используем метод замены переменных.
Обозначим: U-V=N, /9/
где N - целое положительное число.
Из уравнения /9/ имеем:
U=V+N /10/
Из уравнений /8/, /9/ и /10/ имеем:
Аx = N∙ (V+N+V) = N∙(2V+N) =2VN+N2/11/
Из уравнения /11/ имеем:
Аx - N2=2VN/12/
Отсюда:
V=![]() /13/
/13/
Из уравнений /10/ и /13/ имеем:
U = 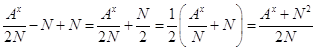 /14/
/14/
Из уравнений /5/, /6/, /13/ и /14/ имеем:
В = ![]() /15/
/15/
С = ![]() /16/
/16/
Из уравнений /13/, /14/, /15/ и /16/ следует: если допустить, что числа V и U могут быть дробными числами, то они могут быть только рациональными дробными числами. Однако никакое рациональное дробное число, возведенное в квадрат, не равно целому числу, тем более:
V2 ≠ (abc…) y; U2 ≠ (def…) z
Поэтому из уравнений /15/ и /16/ следует: необходимым условием для того чтобы числа В и С были целыми, числа V и U должны быть также целыми.
Из уравнений /13/ и /14/ в виде:
V =![]() и U =
и U =![]()
Следует, что число N должно быть делителем числа Аx, т.е. входить как множитель в число Аx. Если число N является составным числом, т.е. является произведением нескольких простых чисел, то оно должно быть произведением множителей, входящих в состав числа Аx.
Из уравнений /13/ и /14/ в виде:
V =![]() иU =
иU =![]()
также следует, что поскольку знаменатели дробей содержат цифру 2, числители должны делиться на 2. Это условие выполняется только в том случае, если числа А и N оба четные или оба нечетные.
Из уравнения /13/ следует, что поскольку число V, исходя из выше принятого условия, должно быть целым положительным числом, должны выполняться условия:
Аx-N2 > 0; или: N2 < Аx и: Аx - N2 >2N.
Установим cоотношения между числами В и С. Разделив уравнение /15/ на уравнение /16/, получим:
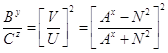 /17/
/17/
Отсюда:
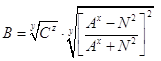 /18/
/18/
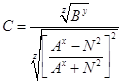 /19/
/19/
Алгебраическое выражение:
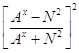 <1 - дробное рациональное число.
<1 - дробное рациональное число.
Алгебраические выражения:
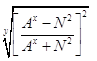 <1 - при y>2 - дробное число. /20/
<1 - при y>2 - дробное число. /20/
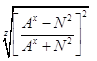 <1 - при z>2 - дробное число. /21/
<1 - при z>2 - дробное число. /21/
Из анализа алгебраических выражений /20/ и /21/ следует, что из одного и того же дробного числа извлекаются корни разных степеней y и z, при этом показатели степени y и z по условию гипотезы Биля взаимно простые числа. Очевидно, что после извлечения корней, по крайней мере, одно из чисел будет иррациональным дробным числом.
Следовательно, одно из чисел B или C или оба - дробные числа.
Таким образом, гипотеза Биля не имеет решения в целых положительных числах.
Похожие работы
... , из уравнения /60/ следует, что любое целое положительное число в квадрате всегда равно разности квадратов одной пары или нескольких пар целых положительных чисел. ВЫВОДЫ Из анализа гипотезы Биля, великой теоремы Ферма и теоремы Пифагора следует, что в основе их лежит одно и тоже уравнение: Аx +Вy= Сz При этом: в уравнении гипотезы Биля показатели степени x, y, z больше 2 и не ...
... = Сz -Вy =U2-V2 /10/ Уравнение /10/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде: Аx = (U-V) ∙ (U+V) /11/ Для доказательства гипотезы Биля используем метод замены переменных. Обозначим: U-V=X /12/ Из уравнения /12/ имеем: U=V+X /13/ Из уравнений /11/, /12/ и /13/ имеем: Аx = X· (V+X+V) =X (2V+X) =2VХ+X2 /14/ Из уравнения ...
... Z 12 30 (15) При рассмотрении вопроса о Пифагоровых тройках не было целью составление таблиц этих троек. Ибо целью этой статьи является показ возможностей алгоритма решения Диофантовых уравнений. Решение уравнения Каталана Уравнение данного вида получается при попытке решения гипотезы Биля. Поэтому решение данного уравнения является как бы леммой гипотезы Биля. Ответ будет ...
... только моделью, но не простой, а моделью, имеющей вполне определенную морфологическую опору. <…> Таков общий объем требований, обеспечивающий достаточное основание гипотез о генетическом родстве <…> языков. Необходимо заметить, что эти требования полностью подтверждаются материалами вышеуказанных языков. <…> Ностратические языки Развитие сравнительно-исторического изучения ...
0 комментариев