Графы и частично упорядоченные множества

Графы и частично упорядоченные множества

Обе эти структуры являются частными случаями бинарных отношений. Пусть задано множество каких-то объектов и из этих объектов по какому-то определенному принципу формируются пары. Например, дано некоторое множество людей, а пары в нем выбираются по такому принципу: первый элемент пары - некий человек, а второй - один из его родителей. При этом один и тот же человек может присутствовать в двух и более парах, например, когда один и тот же человек имеет двоих, троих или более детей. Например, три пары в этом отношении (Иван, Мария), (Дарья, Мария), (Глеб, Мария) означают, что Иван, Дарья и Глеб - дети Марии. В качестве математического примера бинарного отношения можно привести пары, составленные из некоторого множества чисел, при этом первое число в каждой паре меньше второго. Это пример бинарного отношения "меньше". Другой пример: задана некоторая система множеств, а бинарное отношение в этой системе формируется из пар множеств по принципу: первое множество включено во второе множество - это пример бинарного отношения "включение множеств".

Существует много типов бинарных отношений с разными свойствами. Самым общим из этих типов является граф. Это произвольное бинарное отношение, но его особенностью является непривычная терминология - элементы множества, из которого формируются пары, называются вершинами, а сами пары в зависимости от их свойств носят названия ребра или дуги. Графы обычно изображаются не в виде таблицы с двумя колонками (каждая строка такой таблицы представляет пару элементов - вершин), а в виде схемы.

Рассмотрим пример. Пусть задано множество вершин

V = {a, b, c, d, e},

из которого сформировано некоторое множество пар

E = { (a, b), (a, c), (b, d), (c, a), (c, e) }.

Множество пар E, сформированное из множества V вершин, является примером бинарного отношения. Преобразуем это бинарное отношение в схему. Для этого изобразим на листе бумаги все его вершины произвольным образом и соединим эти вершины линиями со стрелками так, чтобы каждая стрелка выходила из первого элемента пары и входила во второй элемент пары (см. рисунок 1). При этом, если окажется, что некоторая пара вершин соединяется стрелкой в одну и в другую сторону, то мы вместо линий со стрелками нарисуем линию без стрелок (для нашего примера это пары (a, c) и (c, a)). С учетом этого дугами в графе являются соединительные линии со стрелками в одну сторону, а ребрами - соединения без стрелок или со стрелками, направленными в обе стороны. Можно считать, что каждое ребро содержат пару разнонаправленных дуг.

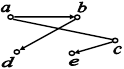
Рис.1

Каждая дуга графа представлена начальной и конечной вершинами. Граф, у которого все связи представлены только ребрами, называется неориентированным графом (или просто графом). Граф, у которого отсутствуют ребра (т.е. все связи имеют только одно направление), называется ориентированным графом, а граф, у которого имеются и ребра, и дуги - смешанным.

Если задан граф G, то выражение G (x), где x - произвольная вершина графа, используется для обозначения множества смежных с ней вершин, т.е. вершин, в которые направлена дуга из x. Например, для графа G на рисунке 8 справедливы следующие равенства:

G (a) = {b, c}; G (b) = {d}; G (c) = {a, e}; G (d) = G (e) = Æ.

Если мы, используя изображение произвольного графа, будем двигаться от вершины к вершине в соответствии с направлением дуг (при этом по ребру можно передвигаться в любую сторону), то последовательность вершин, отмечаемых по мере такого "обхода", называется путем в данном графе. Например для графа G на рисунке 8 существуют следующие пути: (a, b, d); (c, e); (a, c, a, b) и т.д. Пути можно записывать, используя стрелки, например, a®b®d. При этом возможны графы, у которых имеются самопересекающиеся пути, т.е. некоторые вершины и дуги могут в некоторых путях повторяться.

Циклом в графе называется такой путь, когда его начальная и конечная вершина совпадают.

Например, в графе на рисунке 8 имеется один цикл, обусловленный тем, что в нем имеется ребро (a, c). Поэтому цикл можно представить в виде пути (a, c, a). Если в этот граф добавить еще одну дугу (d, a), то в этом случае появится еще одни цикл (d, a, b, d). По сути цикл - это путь без начала и конца, поскольку, "путешествуя" по циклу, мы можем крутиться в нем бесконечное число раз.

Одним из основных в теории графов является понятие достижимости. Вершина yграфа G называется достижимой из вершины x, если в G существует путь из вершины x в вершину y. Часто бывает необходимо определить для каждой вершины графа G множество всех достижимых из нее вершин. Например, для вершины a в графе на рисунке 1 достижимыми являются все вершины этого графа (в том числе и сама вершина a), в то время как из вершины b достижима только одна вершина - d, а для вершины e в данном графе нет вообще достижимых вершин.

Любое бинарное отношение можно представить как граф. Математические свойства графов часто используются при моделировании и анализе сложных систем частично упорядоченных множеств.

Частично упорядоченное множество - один из типов бинарного отношения. Отношение частичного порядка является одним из фундаментальных общематематических понятий и широко используется в теоретической математике, в системах логического вывода и во многих других приложениях. Оно является обобщением таких широко известных бинарных отношений как "меньше или равно" (£) для чисел и "включено или равно" (Í) для множеств. Обозначение "£" часто используется не только для обозначения отношения "меньше или равно" на множестве чисел, упорядоченных по величине, но и для обозначения произвольного отношения частичного порядка. Формально отношение частичного порядка определяется как заданное на множестве X бинарное отношение со следующими свойствами:

рефлексивности: a£a для любого aÎX;

транзитивности: если a£b и b£c, то a£c;

антисимметричности: из a£b и b£a следует a=b,

где a, b и c - произвольные элементы частично упорядоченного множества X.

Среди всех отношений частичного порядка наиболее простым в структурном отношении является линейный порядок, когда для любой пары разных элементов (a, b) множества определено либо a£b, либо b£a. Примерами линейного порядка являются множества чисел, упорядоченных по величине, и множества слов, расположенных в лексикографическом порядке. Их можно по заданному порядку сформировать в виде одной непрерывной последовательности. Например, 2<5<12<19. При линейном порядке все элементы частично упорядоченного множества можно выстроить в одну цепочку по заданному отношению.

В то же время существует немало множеств с отношением частичного порядка, среди которых имеются пары элементов, не связанные этим отношением. К таким множествам, в частности, относятся системы множеств, сравниваемых по включению. Например, если заданы три множества

P = {a, b, c}; Q = {b, d}; R = {a, b, c, d},

то для них линейный порядок установить невозможно, так как множества P и Q несравнимы - ни одно из них не включено в другое. В то же время, если множество Q в этой совокупности заменить на множество Q₁ = {b, c}, то мы получим линейный порядок

Q₁Ì P Ì R или {b, c}Ì{a, b, c}Ì{a, b, c, d}.

Еще одним широко известным отношением частичного порядка является порядок по делимости. Предположим, задано некоторое множество положительных целых чисел (например, D = {1, 2, 3.4, 6, 12}. Тогда будем считать, что для двух чисел x и y верно x£y, если и только если число y делится без остатка на число x.

Для заданного множества D порядок по делимости верен для пар (1,2); (2,4); (3,6) и т.д., Но для некоторых пар (например, (4,6)) такой порядок не соблюдается, так как число 6 не делится без остатка на число 4. Нетрудно убедиться, что отношение порядка по делимости полностью соответствует свойствам частично упорядоченных множеств (рефлексивности, транзитивности и антисимметричности).

В математике известно немало структур, соответствующих частичному порядку. Рассмотрим некоторые общие свойства отношений частичного порядка. Далее в целях сокращения будем использовать вместо термина "частично упорядоченное множество" термин у-множество - своеобразная калька с эквивалентного английского термина poset.

Любое у-множество можно представить как ориентированный граф, в котором дуга a®b между парой элементов означает a£b. Однако не любой ориентированный граф является представлением у‑множества. Чтобы сугубо ориентированный граф представлял правильное у‑множество, необходимо и достаточно чтобы в нем не было циклов.

В математической литературе у-множества обычно изображаются в виде неориентированных графов (рис.2), при этом подразумевается, что предшествующие элементы расположены ниже последующих. Поэтому, если в этих схемах правильно заменить ребра на дуги, то все дуги окажутся направленными снизу вверх.

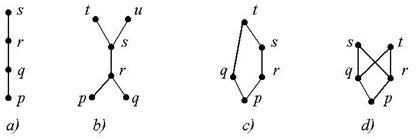
Рис.2

На этих рисунках показаны не все связи между элементами - те, которые следуют из свойства транзитивности (например, связь p®s на каждом из этих рисунков), в них отсутствуют. Такое сокращенное представление у‑множеств без транзитивных связей называется диаграммой Хассе.

В дальнейшем мы будем изображать частично упорядоченные множества не так как это принято в математических работах по алгебре (см. рисунок 2), а в виде ориентированных графов. Определим наименьший и наибольший элементы у-множеств.

Наименьшим элементом у-множества M (если он существует) называется элемент y такой, что y£a для любого элемента aÎM.

Наибольшим элементом у-множества M (если он существует) называется элемент y такой, что a£y для любого элемента aÎM

Например, в у-множестве, изображенном на рис.2, b, нет ни наибольшего, ни наименьшего элементов, наименьший элемент (p) имеется в у‑множествах, изображенных на рис.2, a, c, d, а наибольший элемент имеется только в у‑множествах, изображенных на рисунке 2, a, c.

Если в качестве отношения частичного порядка мы выберем отношение включения, то в этом отношении наименьшим элементом является пустое множество (Æ) (оно включено в любое множество), а наибольшим является универсум (в него включено любое множество системы).

Рассмотрим два очень важных понятия теории у-множеств, которые позволяют существенно облегчить решение некоторых задач анализа рассуждений. Это верхние и нижние конусы. Пусть A - произвольное подмножество у‑множества M (т.е. A Í M). Определим для множества A верхний и нижний конусы.

Нижним конусом  множества A называется множество всех таких элементов x, принадлежащих множеству M, каждый из которых будет меньше или равен (£) относительно любого элемента a, принадлежащего множеству A.

Верхним конусом  множества A называется множество всех таких элементов x, принадлежащих множеству M, для каждого из которых любой элемент из множества A будет меньше или равен (£) ему.

Нижний и верхний конусы можно определять не только для подмножеств, но и для элементов у‑множества M. Если у-множество изображено в виде ориентированного графа, то верхний и нижний конус для любого элемента X можно "вычислить", используя свойство достижимости:

верхний конус элемента X - это множество элементов, в это множество входит сам элемент X и все элементы, достижимые из X;

нижний конус элемента X - это множество элементов, в это множество входит сам элемент X и все элементы, из которых X достижимо.

Например, на множестве чисел M = {2, 4, 5, 7}, упорядоченном по величине, нижним конусом числа 4 является множество {2, 4}, а верхним - {4, 5, 7}. Если рассмотреть у‑множество, показанное на рисунке 9, b, то

={p, q, r} и  = {r, s, t, u}.

Далее мы рассмотрим две теоремы, связанные с конусами. C помощью первой теоремы можно вычислить верхние и нижние конусы не для отдельных элементов, а для некоторых их совокупностей. По смыслу верхние конусы для некоторого множества M элементов должны содержать такие элементы, которые одновременно достижимы из каждого элемента множества M. Аналогично, если вычисляется нижний конус для множества M, то он должен содержать такие элементы, каждый из которых предшествуют любому элементу из множества M. Тогда верхний и нижний конусы для этого множества вычисляются в соответствии со следующей теоремой.

Теорема. Пусть в произвольном у-множестве выбрано некоторое подмножество M = {q₁, q₂,... q_n} его элементов. Тогда

(i) M^D = ÇÇ... Ç;

(ii) M^Ñ=ÇÇ... Ç.

Доказательство. Пусть m_i - произвольный элемента множества M^D. Чтобы для каждого q_k (q_kÎ M) соблюдалось условие q_k £ m_i, необходимо и достаточно, чтобы элемент m_i содержался в верхнем конусе каждого из элементов множества M. А это означает, что элемент m_i содержится в пересечении ÇÇ... Ç верхних конусов всех этих элементов. Аналогично, если m_i - произвольный элемента множества M^Ñ, то для каждого q_k (q_kÎ M) соблюдается условие m_i £ q_k, а это означает, что элемент m_i содержится в нижнем конусе каждого из элементов множества M. Следовательно, все элементы множества M^Ñ должны находиться в пересечении ÇÇ... Ç нижних конусов. Конец доказательства.

Для лучшего понимания соотношений, связанных с конусами, рассмотрим граф, изображающий диаграмму Хассе некоторого у-множества (рисунок 3).

Рис.3

По этому рисунку можно, используя свойство достижимости, легко вычислить верхние и нижние конусы любых элементов. Например,

R^D= {R, G, F, Q}

(элемент R содержится в верхнем конусе по определению, а остальные элементы введены как достижимые из R);

M^D= {M, N, G, F, Q}; D^D= {D}; C^D= {C, D}; D^Ñ = {D, C, A}

(элемент D содержится в нижнем конусе по определению, а элементы C и A введены в нижний конус, поскольку из них достижим элемент D);

R^Ñ = {R, A}; M^Ñ = {M}; C^Ñ = {C, A}, G^Ñ = {G, M, R, A}.

Зная верхние или нижние конусы элементов, можно по теореме легко вычислить соответственно верхние и нижние конусы для множеств, состоящих их этих элементов. Например,

{R, M}^D = R^DÇ M^D= {R, G, F, Q}Ç{M, N, G, F, Q}={G, F, Q};

{R, C}^D = R^DÇ C^D= {R, G, F, Q}Ç{C, D}= Æ

(посмотрев на рисунок 10, можно убедиться, что в графе нет ни одной вершины, которая достижима как из R, так и из C);

{R, M}^Ñ = R^ÑÇ M^Ñ= {R, A}Ç{M}= Æ;

{R, C}^Ñ = R^ÑÇ C^Ñ= {R, A }Ç{C, A}= {A}.

Рассмотрим еще одно соотношение, связанное с конусами.

Теорема 2. Пусть r и q - различные элементы у-множества, при этом r £ q. Тогда для верхних и нижних конусов этих элементов соблюдаются соотношения Í и Í.

Доказательство. Данные соотношения следуют из определений верхних и нижних конусов. Если r £ q, то это означает, что q содержится в  и, следовательно, все элементы из  также содержится в . В то же время в нижних конусах наоборот: если r £ q, то это означает, что r содержится в  и, следовательно, все элементы из  также содержится в . Конец доказательства.

Например, для у-множества, изображенного на рисунке 3, элементы A и G - сравнимы, т.е. A £ G (элемент A предшествует элементу G). Построим верхние и нижние конусы этих элементов:

A^D = {A, C, D, R, G, F, Q }; G^D = {G, F, Q }; A^Ñ = {A}; G^Ñ = {G, R, A, M}.

Сравнивая эти конусы по включению, мы увидим, что в соответствии с теоремой 2 соблюдаются следующие соотношения: G^D Í A^D и A^Ñ Í G^Ñ. Если же выбрать для анализа пару элементов, для которых отношение £ не имеет места (например, элементы Q и N на рисунке 3), то мы увидим, что для них, соотношения, сформулированные в теореме 2, не верны.

Для анализа E-структур очень важными являются еще два понятия - минимальные и максимальные элементы. Суть в том, что они существенно отличаются от наименьшего и наибольшего элементов. Начнем с минимальных элементов. Как мы уже знаем, если в структуре существует наименьший элемент, то он меньше любого другого элемента этого у‑множества. Но существуют элементы (в алгебре их иногда называют атомами), которые больше наименьшего, но при этом обладают одним удивительным свойством. Предположим, что элемент A - атом, а X_i произвольный элемент этого у-множества, кроме наименьшего. Тогда при сравнении атома A с любым элементом X_i возможны только два варианта:

1) A £ X_i либо 2) элементы A и X_i несравнимы. Атомы в отличие от наименьших элементов называются минимальными элементами.

Чтобы лучше понять это рассмотрим рисунок 10. Видно, что в этом у-множестве наименьшего элемента не существует, так как ни один элемент в нем не обладает тем свойством что он предшествует любому элементу. Например, элементу A не предшествует ни один элемент, но при этом он сам не предшествует таким элементам как M и N (т.е. пары (A, N) и (A, M) не сравнимы, так как неизвестно, какой из элементов в каждой из этих пар является предшественником другого). Поэтому элемент A можно считать минимальным (но не наименьшим!) элементом. Нетрудно видеть, что в этой же структуре есть еще один минимальный элемент - M, который обладает теми же свойствами, что и элемент A.Т. е. в этой структуре существуют два минимальных элемента (хотя наименьшего в ней нет). Если в структуре имеется наименьший элемент, то в этом случае минимальными элементами являются другие элементы, которые больше наименьшего, но при этом непосредственно примыкают к нему.

Максимальные элементы в у-множествах определяются аналогично. Максимальные элементы (в алгебре они иногда называются коатомами) - это элементы, обладающие следующими свойствами:

1) если наибольший элемент существует, то максимальные элементы непосредственно предшествуют наибольшему элементу;

2) любой элемент у‑множества (кроме наибольшего) либо предшествует максимальному элементу, либо не сравним с ним.

Посмотрев на у-множество на рисунке 10, можно с учетом этих свойств легко определить его максимальные элементы: это D, F и Q.