Содержание
1. Введение в анализ и дифференциальное исчисление функции одного переменного
2. Дифференциальное исчисление функций и его приложение
3. Интегральное исчисление функции одного переменного
1. Введение в анализ и дифференциальное исчисление функции одного переменного
1. Вычислить предел: 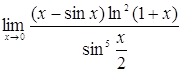 .
.
Решение.
При ![]() имеем
имеем
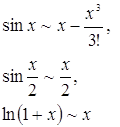
Следовательно,
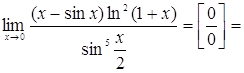
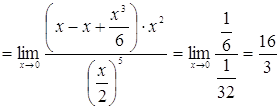
2. Найти асимптоты функции: ![]() .
.
Решение.
Очевидно, что функция не определена при ![]() .
.
Отсюда получаем, что
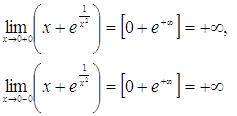
Следовательно, ![]() – вертикальная асимптота.
– вертикальная асимптота.
Теперь найдем наклонные асимптоты.
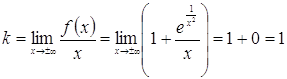
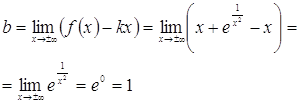
Следовательно, ![]() – наклонная асимптота при
– наклонная асимптота при ![]() .
.
3. Определить глобальные экстремумы: ![]() при
при ![]() .
.
Решение.
Известно, что глобальные экстремумы функции на отрезке достигаются или в критических точках, принадлежащих отрезку, или на концах отрезка. Поэтому сначала находим ![]() .
.
![]() .
.
А затем находим критические точки.
![]()
![]()
![]()
Теперь найдем значение функции на концах отрезка.
![]() .
.
Сравниваем значения и получаем:
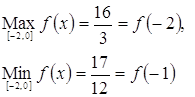
4. Исследовать на монотонность, найти локальные экстремумы и построить эскиз графика функции: ![]() .
.
Решение.
Сначала находим ![]() .
.
![]() .
.
Затем находим критические точки.
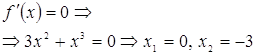
| x |
| –3 |
| 0 |
|
|
| – | 0 | + | 0 | + |
|
| убывает | min | возрастает | возрастает | возрастает |
Отсюда следует, что функция
возрастает при ![]() ,
,
убывает при ![]() .
.
Точка ![]() – локальный минимум.
– локальный минимум.
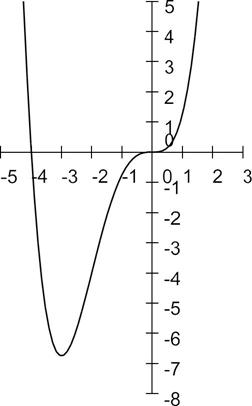
5. Найти промежутки выпуклости и точки перегиба функции: ![]() .
.
Решение
Чтобы найти промежутки выпуклости и точки перегиба, найдем вторую производную функции.
![]() .
.
![]() .
.
![]() .
.
x |
| –2 |
| 1 |
|
|
| – | 0 | – | 0 | + |
|
| вогнутая | перегиб | выпуклая | перегиб | вогнутая |
Отсюда следует, что функция
выпуклая при ![]() ,
,
вогнутая при ![]() .
.
Точки ![]() ,
, ![]() – точки перегиба.
– точки перегиба.
2. Дифференциальное исчисление функций и его приложение»
1. Провести полное исследование свойств и построить эскиз графика функции ![]() .
.
Решение.
1) Область определения функции
![]() .
.
2) Функция не является четной или нечетной, так как
![]() .
.
3) Теперь найдем точки пересечения с осями:
а) с оx: ![]() , б) с oy
, б) с oy ![]() .
.
4) Теперь найдем асимптоты.
а) 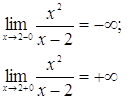
А значит, ![]() является вертикальной асимптотой.
является вертикальной асимптотой.
б) Теперь найдем наклонные асимптоты
![]()
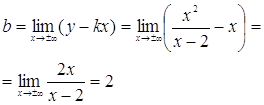
Отсюда следует, что
![]() является наклонной асимптотой при
является наклонной асимптотой при ![]() .
.
5) Теперь найдем критические точки
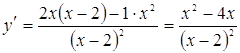
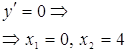
![]() не существует при
не существует при ![]() .
.
6) 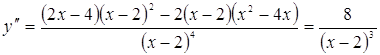
![]()
![]() не существует при
не существует при ![]()
| x |
| 0 |
| 2 |
| 4 |
|
|
| + | 0 | – | Не сущ. | – | 0 | + |
|
| – | – | – | Не сущ. | + | + | + |
| y | возрастает выпуклая | max
| убывает выпуклая | не сущ. | убывает вогнутая | min
| возрастает вогнутая |
Построим эскиз графика функции ![]()
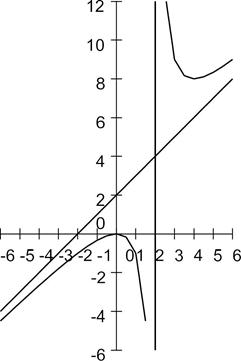
2. Найти локальные экстремумы функции ![]() .
.
Решение.
Сначала найдем частные производные
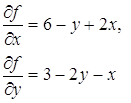
Известно, что необходимым условием существования экстремума является равенство нулю частных производных.
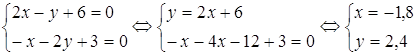
То есть мы получили одну критическую точку: ![]() . Исследуем ее.
. Исследуем ее.
Далее проведем исследование этой точки.
Для чего найдем предварительно частные производные второго порядка
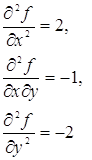
Для точки ![]() :
:
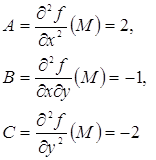
![]() .
.
Следовательно, точка ![]() не является точкой экстремума.
не является точкой экстремума.
Это означает, что точек экстремума у функции
![]() нет.
нет.
3. Определить экстремумы функции ![]() , если
, если ![]() .
.
Решение.
Сначала запишем функцию Лагранжа
![]() .
.
И исследуем ее
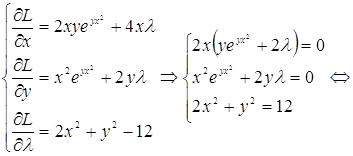
(Учитываем, что по условию ![]() )
)
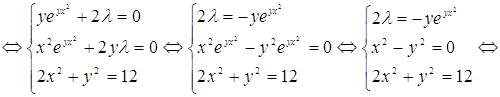
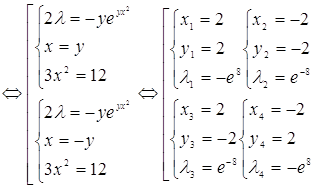
То есть мы получили четыре критические точки.
В силу условия ![]() нам подходит только первая
нам подходит только первая ![]() .
.
Исследуем эту точку.
Вычислим частные производные второго порядка:
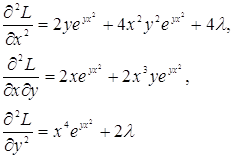
Отсюда получаем, что
![]()
Теперь продифференцируем уравнение связи
![]() .
.
Для точки ![]()
![]()
Далее получаем
![]()
![]()
![]()
![]()
То есть мы получили отрицательно определенную квадратичную форму.
Следовательно, ![]() – точка условного локального максимума.
– точка условного локального максимума.
![]() .
.
3. Интегральное исчисление функции одного переменного
1–3. Найти неопределенный интеграл
1. ![]() .
.
Решение.
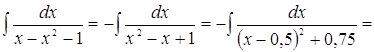
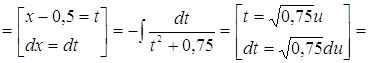
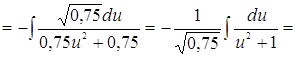
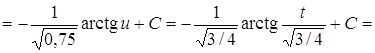
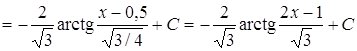 .
.
2. ![]() .
.
Решение.
![]()
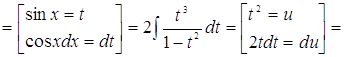
![]()
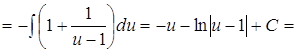
![]()
![]() .
.
3. ![]()
Решение.
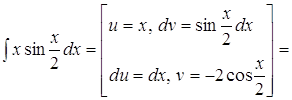
![]() .
.
4. Вычислить 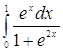 .
.
Решение.
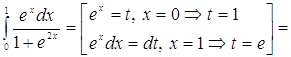
![]() .
.
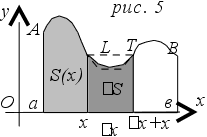
5. Определить площадь плоской фигуры, ограниченной кривыми
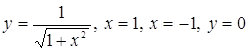 .
.
Решение.
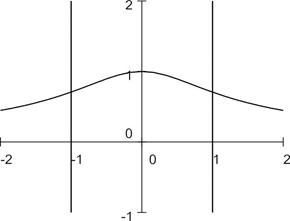
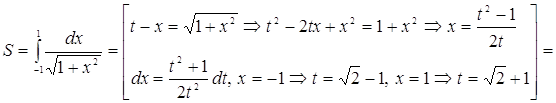
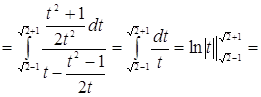
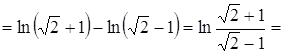
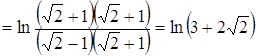 .
.
Похожие работы
... = [х ln х] – х(dх/х) = = [х ln х] – [х] = 2 ln2 – 1 = ln4 – 1 3.Исторические сведения о возникновении и развитии основных понятий. В математике XVII в. самым большим достижением справедливо считается изобретение дифференциального и интегрального исчисления. Сформировалось оно в ряде сочинений Ньютона и Лейбница и их ближайших сотрудников и учеников. Введение в математику методов анализа ...
... некоторых математических теорем Выведем из физических соображений некоторые ограничения на функцию, которая может служить законом движения макроскопического тела, а затем сравним их с условиями основных теорем дифференциального исчисления. (А) Начнем с простого соображения о том, что реальный физический эксперимент имеет свое начало и конец, т.е. протекает за конечный отрезок времени. В силу ...
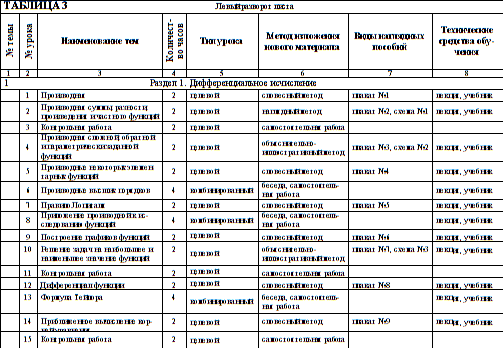
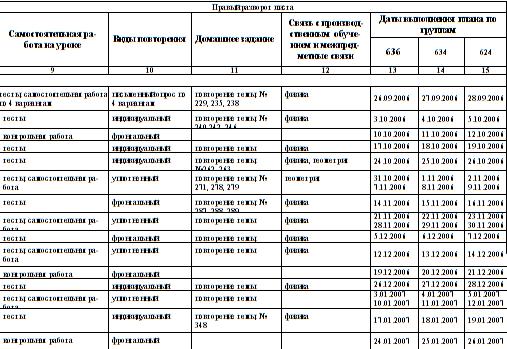
... 2 11 Контрольная работа 2 2 12 Дифференциал функции 2 2 13 Формула Тейлора 4 2 2 14 Приближенное вычисление корней уравнений 2 2 15 Контрольная работа 2 2 На изучение раздела "Дифференциальное исчисление" в предмете "Высшая математика", дается 36 часов. Из них: 22 часа теоретических занятий и 14 часов посвящены практическому изучению. Календарно- ...
... Спорщики возьмут в руки перья и, сказав: “Начнем вычислять” - примутся за расчеты. Как уже отмечалось, Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Об этом свойстве хороню знал и ...
0 комментариев