Министерство Образования Российской Федерации
ИрГТУ
Кафедра АПП
Курсовая работа по математике
Выполнил: студент группы АТП-05-1
Поверил: профессор
Баев А. В.
Иркутск
2007 г
Задание.
1. Для заданной электрической цепи составить дифференциальные уравнения при входном воздействии типа скачка.
2. Применить к полученному уравнению преобразование Лапласа при нулевых начальных условиях.
3. Решить уравнение операторным методом.
4. Построить переходный процесс.
5. Записать выражение и построить частотные характеристики цепи: АЧХ, ФЧХ, ДЧХ, МЧХ и АФЧХ (амплитудно-фазовую характеристику).
6. Описать динамику вашей цепи в терминах пространства состояния.
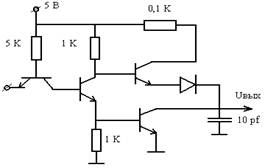
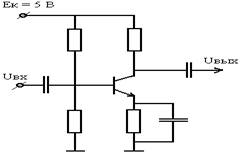
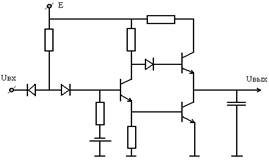
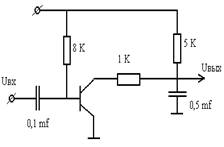
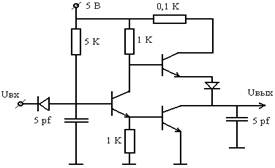
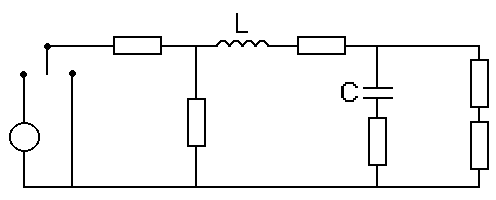
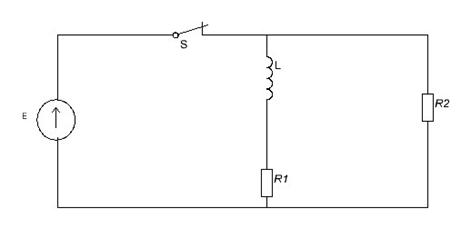
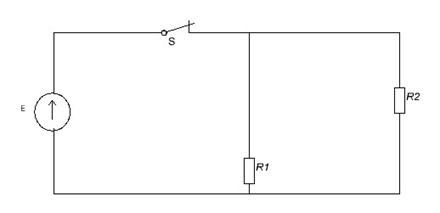
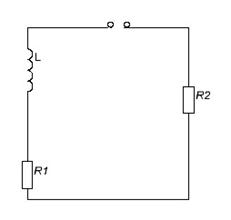
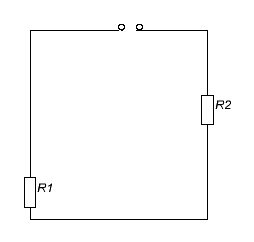
Схема электрической цепи
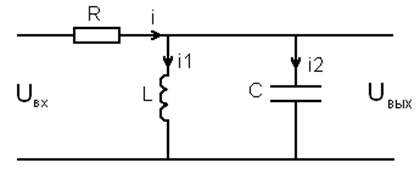
Дано:
R = 5
L = 10
C = 12
![]()
![]()
![]()
![]()
![]()
![]()
![]() ;
; ![]()
![]()
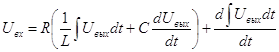
При подстановке данных получаем окончательное дифференциальное уравнение:
![]()
Применим преобразование Лапласа и запишем передаточную функцию для данной цепи
![]()
![]()
Решаем характеристическое уравнение:
![]()
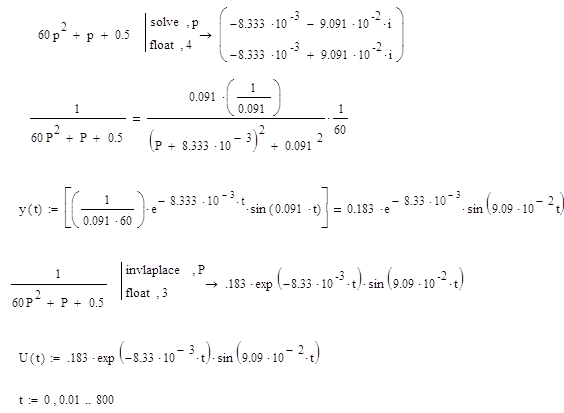
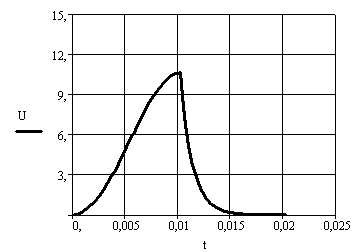
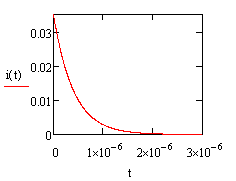
График переходного процесса
![]()
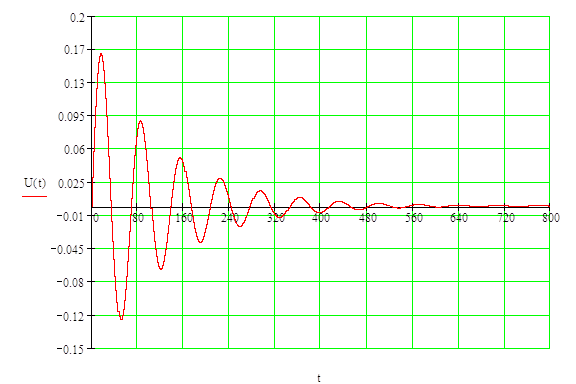
Заменим P = jω, получая комплексную переменную:
![]()
Решаем алгебраически:
АФЧХ : 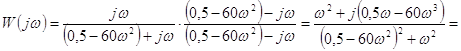
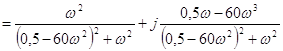
ДЧХ : 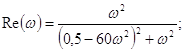
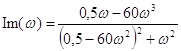
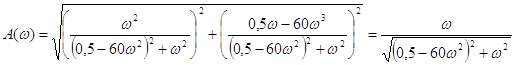
ФЧХ : 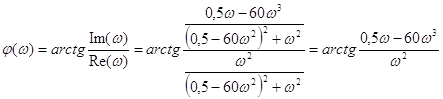
С помощью MathCAD строим все виды характеристик цепи:
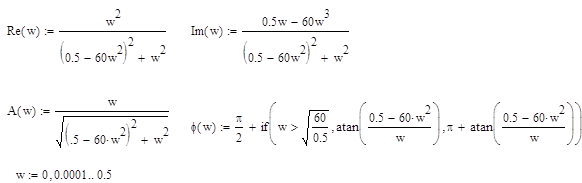
Графики частотных характеристик цепи:
ДЧХ и МЧХ:
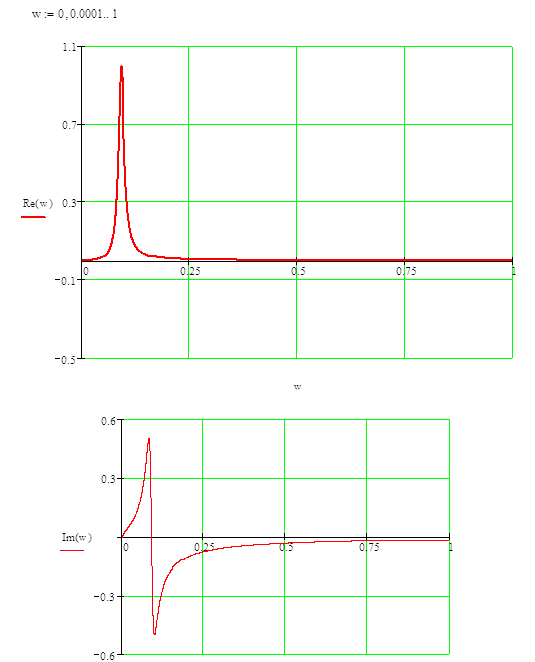
АЧХ: 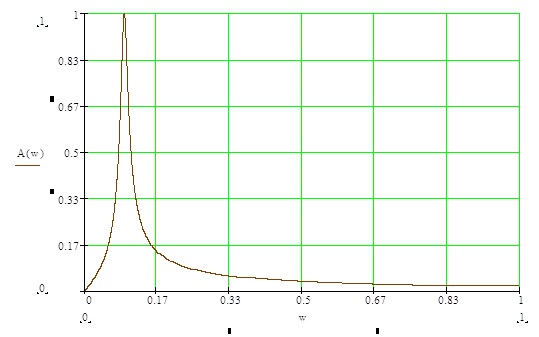
ФЧХ:
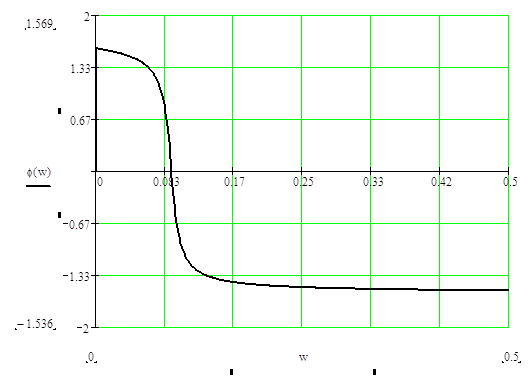
АФЧХ:
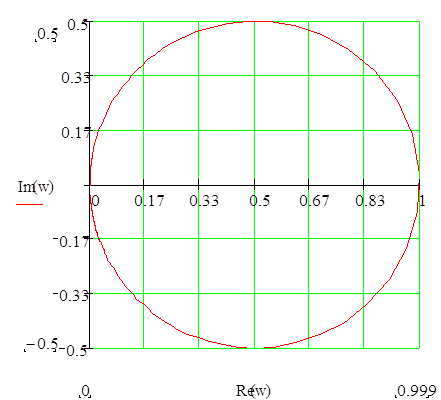
Опишем динамику нашей цепи в терминах пространства состояния.
Компактная форма:
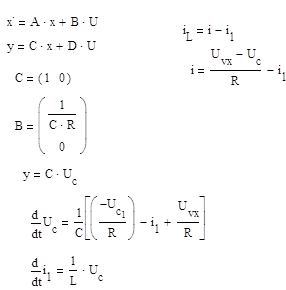
Составляем матрицу A:
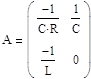
Составляем матрицу единичную матрицу Ep:
![]()
Выражение для передаточной функции:
![]()
Составляем матрицу из алгебраического дополнения:
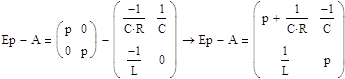
Составляем транспонированную матрицу:
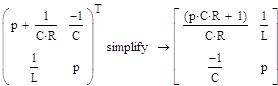
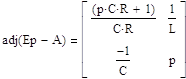
Находим определитель ∆
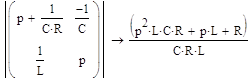
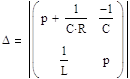
![]()
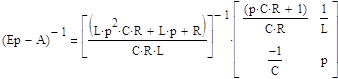
Выражение для передаточной функции:
![]()
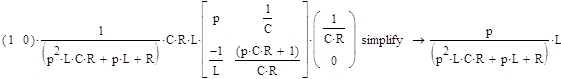
При подстановке данных, получаем:
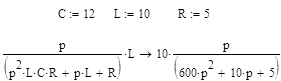
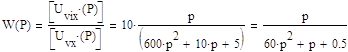
Дискретная форма.
Передаточная функция равна:
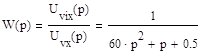
Находим корни корни характеристического уравнения:
![]()
Из таблицы оригиналов и значений:
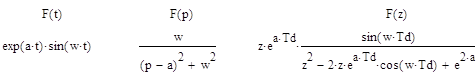
Произведем подстановку данных:
![]()
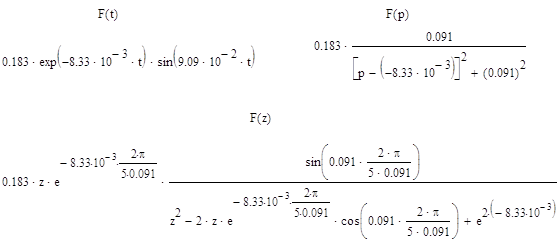
Разделим числитель и знаменатель на z в max степени:
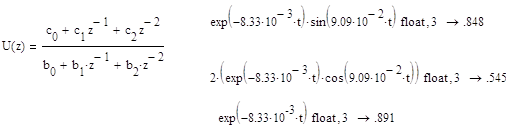
Следовательно:
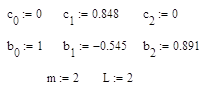
где m- максимальная степень z, L- максимальная степень z в знаменателе:
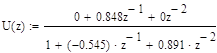
Находим, целю часть:
![]()
Следовательно:
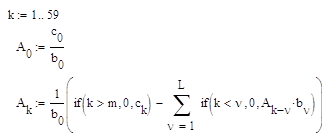
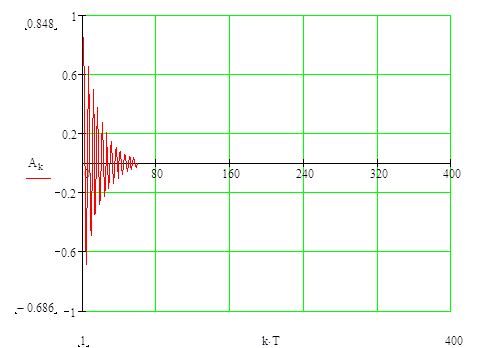
График дискретной функции :
Похожие работы
... цепи для передачи и преобразования электрической энергии и цепи для передачи и преобразования информации. Основные понятия и элементы линейных пассивных электрических цепей Электрический ток и напряжение - основные величины, характеризующие состояние электрических цепей. Электрический ток в проводнике есть упорядоченное перемещение электрических зарядов. Ток оценивают интенсивностью или ...
... к расчету. ¨ В оглавлении указываются названия разделов и номера страниц, соответствующие началам разделов. ¨ Во введении кратко рассматривается общенаучное значение теории электрических цепей (ТЭЦ) для изучения электромагнитных явлений и их практического приложения. Описываются связи ТЭЦ с соответствующими разделами математики и физики, а также с различными ...
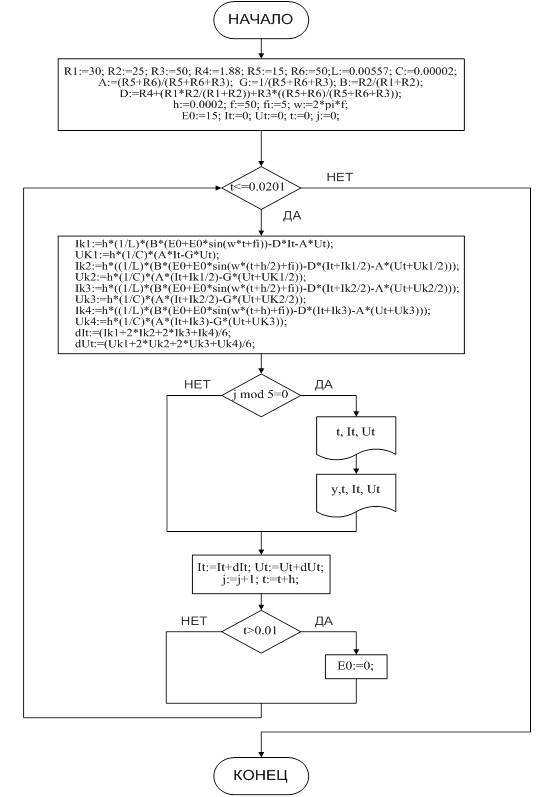
... колебаний Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Ом - резистор Гц - линейная частота с. - текущее время с. - текущее время Рад - фаза 1.3 Описание работы электрической цепи В начальный момент времени ключ находится в положении . При этом цепь разомкнута, напряжение на конденсаторе и ток на катушке равны нулю . Происходит первое переключение ключа, ...
... i(t) либо постоянная величина i0, либо синусоидальные токи in, то для их определения применяют известные методы расчета цепей постоянного и переменного синусоидального токов. Рассчитать формы и спектры сигналов при нелинейных преобразованиях Исходные данные: U0=0,5 В, U1=1 В, Um=1,5 В, S=16 мА/В, T=11 мкс 1. Рассчитаем угол отсечки θ в радианах и градусах cos θ= ...
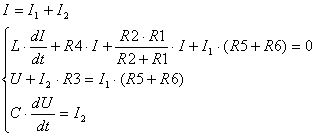

0 комментариев