Навигация
5.3. Анотації
На останніх сторінках автореферату розміщують анотації українською, російською й англійською мовами. На вибір здобувача анотація англійською чи російською мовою повинна бути розгорнутою інформацією, обсягом 2 сторінки машинописного тексту (до п'яти тисяч друкованих знаків), про зміст і результати дисертаційної роботи, а дві інші – обсягом до 0,5 сторінки машинописного тексту (до 1200 друкованих знаків) – ідентичного змісту інформація про основні ідеї та висновки дисертації. Анотації складаються за формою, яка має такий зміст: прізвище та ініціали здобувача; назва дисертації;
вид дисертації (рукопис, монографія) І науковий ступінь; спеціальність (шифр і назва); установа, де відбудеться захист; місто, рік;
основні ідеї, результати та висновки дисертації. Викладення матеріалу в анотації повинно бути стислим і точним. Належить використовувати синтаксичні конструкції, притаманні мові ділових документів, уникати складних граматичних зворотів. Необхідно використовувати стандартизовану термінологію, уникати маловідомих термінів і символів,
Після кожної анотації наводять ключові слова відповідною мовою. Ключовим словом називається слово або стійке словосполучення із тексту анотації, яке з точки зору інформаційного пошуку несе смислове навантаження. Сукупність ключових слів повинна відображувати поза контекстом основний зміст наукової праці. Загальна кількість ключових слів має бути не меншою трьох і не більшою десяти.
Ключові слова подають у називному відмінку, друкують у рядок, через кому.
5.4. Оформлення автореферату
Примірники автореферату, які здобувач подає до спеціалізованої вченої ради разом з іншими документами та дисертацією, друкують за тими самими правилами, встановленими цим додатком для друкування дисертацій, із урахуванням певних особливостей.
За обсягом автореферат (без обкладинки й анотацій) не може бути меншим 1,3 авторського аркуша, а також перевищувати 1,9 авторського аркуша для докторської та, відповідно, не менше ніж 0,7 авторського аркуша та не перевищувати 0,9 авторського аркуша для кандидатської дисертації при друкуванні через 1,5 інтервалу на друкарській машині або з одинарним інтервалом із використанням текстового редактора Word з розміщенням від 40 до 44 рядків на сторінці.
На лицьовій стороні обкладинки автореферату подаються; назва організації, спеціалізована вчена рада якої прийняла дисертацію до захисту; індекс УДК; прізвище, ім'я, по батькові здобувача; назва дисертації; шифр І найменування спеціальності за переліком спеціальностей наукових працівників; підзаголовок "Автореферат дисертації на здобуття наукового ступеня доктора (кандидата) (галузь науки)"; місто, рік. (форма 6).
На зворотному боці обкладинки автореферату вказується організація, в якій виконане дисертаційне дослідження; науковий ступінь, вчене звання, прізвище й ініціали наукового керівника і (або) консультанта, його місце роботи та посада; наукові ступені, вчені звання, місця роботи, посади, прізвища й ініціали офіційних опонентів; дата, час проведення захисту, шифр спеціалізованої вченої ради та адреса організації, при якій Ті створено; бібліотека, в якій можна ознайомитися з дисертацією; дата розсилання автореферату; підпис вченого секретаря спеціалізованої вченої ради (форма 7). Серед учених звань наукового керівника й опонентів не рекомендується згадувати їх членство в громадських (не державних) академіях наук.
Автореферат не має титульного аркуша.
Номери сторінок проставляються в центрі верхнього поля сторінки. Нумерація починається з цифри 1 на першій сторінці, де міститься загальна характеристика роботи.
Структурні частини автореферату не нумерують, їх назви друкують великими літерами симетрично тексту.
5.5. Видання автореферату
Автореферат дисертації виготовляють друкарським способом і видають у вигляді брошури тиражем 100 примірників.
Формат видання 145x215 мм (формат паперу і частка аркуша 60x90/16) з друкуванням тексту на обох боках аркуша.
На авторефераті повинні бути вказані випускні дані друкарні або іншої установи, де друкувався автореферат, згідно з міждержавним стандартом. Відповідальність за наявність випускних даних та за обов'язкове розсилання авторефератів несе спеціалізована вчена рада.
2. Особливості математичного моделювання в економіці
Мистецтво побудови економіко-математичної моделі полягає в тому, щоб узгоджувати якомога більшу лаконічність у її математичному описі з достатньою адекватністю та точністю модельного відтворення тих сторін аналізованої економічної реальності, які, власне, і цікавлять дослідника згідно з цілями та взятими гіпотезами.
Якщо йдеться про математичну модель, що описує механізм функціонування певної гіпотетичної економічної чи соціально-економічної системи, то таку модель називають економіко-математичною чи просто економічною.
Моделювання економіки як науковий напрям сформувався у 60-ті роки ХХ століття, хоча має давню й багату передісторію. У його основу, окрім економічних, покладено низку фундаментальних дисциплін (математику, теорію ймовірностей, теорію систем, інформатику, статистику, теорію автоматичного управління тощо).
Під економіко-математичною моделлю розуміють концентроване вираження найсуттєвіших економічних взаємозв’язків досліджуваних об’єктів (процесів) у вигляді математичних функцій, нерівностей і рівнянь.
Наголосимо, що математична модель – це об’єкт, котрий створюється системним аналітиком для отримання нових знань про об’єкт-оригінал і відбиває лише суттєві (з погляду системного аналітика) властивості об’єкта-оригіналу. Аналізуючи сутність зазначеного вище, можна зробити, зокрема, такі висновки:
а) будь-яка модель є суб’єктивною, вона несе в собі характерні риси індивідуальності системного аналітика;
б) будь-яка модель є гомоморфною, тобто в ній відбиваються (віддзеркалюються) не всі, а лише суттєві властивості об’єкта-оригіналу виходячи з цілей дослідження, узятої системи гіпотез тощо;
в) можливе існування множини моделей одного й того самого об’єкта-оригіналу, які відрізняються цілями дослідження, ступенем адекватності тощо.
Модель вважається адекватною об’єкту-оригіналу, якщо вона з достатнім ступенем наближення, на рівні розуміння системним аналітиком модельованого процесу відображає закономірності процесу функціонування реальної економічної системи у зовнішньому щодо об’єкта дослідження середовищі.
Проникання математики в економічну науку пов’язане з подоланням значних труднощів. У цьому частково була "винна" математика, яка розвивалась упродовж декількох століть здебільшого з огляду на потреби фізики і техніки. Але головні причини криються все ж у природі економічних процесів, у специфіці економічної науки. Більшість об’єктів, що їх вивчає економічна наука, можуть бути охарактеризовані поняттям "складна система". Найпоширенішим є розуміння системи як сукупності елементів, що перебувають у взаємодії та утворюють певну цілісність, єдність. Важливою якістю будь-якої системи є емерджентність – наявність таких властивостей, які не притаманні жодному з її елементів, які складають систему. Тому у вивченні економічної системи недостатньо користуватися методом поділу її на елементи з наступним вивченням цих елементів окремо. Одна з труднощів економічних досліджень полягає у тому, що майже не існує економічних об’єктів, які можна було б розглядати як окремі (несистемні) елементи.
Складність системи визначається кількістю її елементів, зв’язками між цими елементами, а також зв’язками між системою і середовищем. Економіка країни має всі ознаки дуже складної системи. Вона об’єднує величезну кількість елементів, відзначається різноманітністю внутрішніх зв’язків і зв’язків з іншими системами (природне середовище, економіка іншої країни тощо). У народному господарстві взаємодіють природні, технологічні, соціальні процеси, діють об’єктивні й суб’єктивні чинники, домінуючий вплив справляють культура, система етичних цінностей, ментальність тощо.
Складність економіки інколи розглядалась як обґрунтування неможливості її моделювання, вивчення засобами математики. Але така думка в принципі помилкова. Моделювати можна об’єкти будь-якої природи і складності. І якраз складні об’єкти становлять найбільший інтерес для моделювання; саме тут моделювання може принести результати, котрі не можна одержати іншими способами дослідження.
І хоча не можна вказати абсолютні межі формалізованості економічних проблем, завжди існуватимуть ще неформалізовані проблеми, а також ситуації, де на даному етапі розвитку науки математичне моделювання є недостатньо ефективним.
Під моделюванням розуміють процес побудови, вивчення й використання моделей. Він тісно поєднаний з такими категоріями, як абстракція, аналогія, гіпотеза тощо.
Процес моделювання включає три системотвірних елементи:
· суб’єкт дослідження (системний аналітик);
· об’єкт дослідження;
· модель, яка опосередковує відносини між об’єктом, який вивчається, та суб’єктом, який пізнає (системним аналітиком).
Головним гальмом для практичного застосування математичного моделювання в економіці є проблема наповнення розроблених моделей конкретною та якісною інформацією. Точність і повнота первинної інформації, реальні можливості її збору й опрацювання справляють визначальний вплив на вибір типів прикладних моделей. З другого боку, завдання моделювання економіки висувають нові вимоги до системи інформації.
Залежно від модельованих об’єктів і призначення моделей використовувана в них вихідна інформація має суттєво відмінний характер і походження. Вона може бути розподіленою на дві категорії: щодо минулого розвитку та сучасного стану об’єктів (економічне спостереження й опрацювання) і про майбутній розвиток об’єктів, які включають дані про очікувані зміни, їхні внутрішні параметри та зовнішні умови (прогнози). Друга категорія інформації є результатом самостійних досліджень, які також можуть проводитися за допомогою моделювання.
Методи економічних спостережень і використання результатів цих спостережень розробляються економічною статистикою. З огляду на це варто визначити лише специфічні проблеми економічних спостережень, які стосуються моделювання економічних процесів. В економіці чимало процесів, які є масовими: вони характеризуються закономірностями, які не проявляються на підставі лише одного чи кількох спостережень. Тому моделювання в економіці має спиратися на масові спостереження.
Друга проблема породжується динамічністю економічних процесів, мінливістю їхніх параметрів і структурних відношень. Унаслідок цього економічні процеси доводиться постійно вивчати, здійснювати їх моніторинг, бо необхідно мати постійно приплив нових даних. Оскільки спостереження за економічними процесами й опрацювання емпіричних даних звичайно забирають досить багато часу, то, будуючи математичні моделі економіки, необхідно коригувати вихідну інформацію з урахуванням того, що вона надходить із запізненням на деякий інтервал часу.
Дослідження кількісних відношень економічних процесів і явищ спирається на економічні виміри. Точність проведення вимірювань значною мірою впливає на точність кінцевих результатів кількісного аналізу. Тому необхідною умовою використання математичного моделювання є вдосконалення вимірювачів. Застосування математичного моделювання загострило проблему вимірювання і кількісного зіставлення різних аспектів і явищ соціально-економічного розвитку та повноти одержуваних даних, захист їх від навмисних і технічних викривлень (деформації).
У процесі моделювання виникає взаємодія "первинних" і "вторинних" економічних вимірювань. Будь-яка модель народного господарства спирається на певну систему економічних вимірювачів (продукції, ресурсів тощо). Одночасно одним із важливих результатів народногосподарського моделювання є одержання нових (вторинних) економічних вимірювачів – економічно обґрунтованих цін на продукцію різних галузей, оцінки ефективності різноякісних природних ресурсів, вимірювачів суспільної корисності продукції. Однак ці вимірювачі чутливі до недостатньо обґрунтованих (деформованих) первинних вимірювачів, що спонукає розробляти особливу методику коригування первинних вимірювачів для господарських моделей.
З погляду "інтересів" моделювання економіки сьогодні найбільш актуальними проблемами вдосконалення економічних вимірювачів є: оцінка результатів інтелектуальної діяльності (особливо в царині науково-технічних розробок, індустрії інформатики); побудова узагальнюючих показників соціально-економічного розвитку; вимірювання ефектів зворотних зв’язків (вплив господарських і соціальних механізмів на ефективність виробництва).
Для методології планування важливе значення має поняття невизначеності економічного розвитку. В дослідженнях з економічного прогнозування і планування розрізняють два типи невизначеності: "істинну", зумовлену властивостями економічних процесів, і інформаційну, пов’язану з неповнотою і неточністю наявної інформації про ці процеси. Істинну невизначеність не можна плутати з об’єктивним існуванням різних варіантів економічного розвитку і можливості свідомого вибору з-поміж них ефективних варіантів. Ідеться про принципову неможливість точного вибору єдиного оптимального варіанта.
У розвитку економіки невизначеність викликається двома головними причинами. По-перше, перебіг планованих і керованих процесів, а також зовнішній вплив на ці процеси не можуть бути точно передбаченими через вплив випадкових чинників і обмеженість людського пізнання в кожний момент. Особливо характерно це для прогнозування науково-технічного прогресу, потреб суспільства, економічної поведінки. По-друге, загальнодержавне планування й управління не лише не всеохоплюючі, але і не всесильні, а наявність множини самостійних економічних суб’єктів з особливими інтересами не дозволяє точно передбачити результати їх взаємодії. Неповнота і неточність інформації про об’єктивні процеси й економічну поведінку підсилює істинну невизначеність.
На перших етапах дослідження з моделювання економіки застосовувались в основному моделі детермінованого типу. У цих моделях усі параметри вважалися точно відомими. Однак детерміновані моделі не можна сприймати механічно й ототожнювати з моделями, які позбавлені всіх ступенів вибору (можливості вибору) і мають єдиний допустимий розв’язок. Класичним прикладом жорстко детермінованих моделей є оптимізаційна модель народного господарства, застосовувана для визначення найкращого варіанта економічного розвитку серед множини допустимих варіантів.
Унаслідок накопичення досвіду використання жорстко детермінованих моделей були створені реальні можливості успішного застосування більш досконалої методології моделювання економічних процесів, які враховують стохастику і невизначеність. Тут можна виокремити два основних напрями дослідження. По-перше, вдосконалюється методика використання моделей жорстко детермінованого типу: проведення багатоваріантних розрахунків і модельних експериментів з варіацією конструкції моделі та її вихідних варіантів; визначення стійкості та надійності одержуваних рішень, виокремлення зони невизначеності; включення в модель змінних щодо резервів, застосування прийомів, які підвищують пристосовуваність економічних рішень до ймовірних і непередбачуваних ситуацій. По-друге, формують моделі, які безпосередньо відображають стохастику і невизначеність економічних процесів і використовують відповідний математичний апарат: теорію ймовірностей і математичну статистику, теорію гри і статистичних рішень, теорію масового обслуговування, стохастичне програмування, теорію випадкових процесів, теорію нечітких множин тощо.
Математичні моделі економічних процесів і явищ коротко можна назвати економіко-математичними моделями. Для класифікації цих моделей використовують різні класифікаційні ознаки.
За цільовим призначенням економіко-математичні моделі поділяються на теоретико-аналітичні, що використовуються під час дослідження загальних властивостей і закономірностей економічних процесів, і прикладні, що застосовуються у розв’язанні конкретних економічних задач (моделі економічного аналізу, прогнозування, управління).
Економіко-математичні моделі можуть призначатися для дослідження різних сторін функціонування народного господарства (зокрема, його виробничо-технологічної, соціальної, територіальної структури) і його окремих частин. У класифікації можна виокремити моделі народного господарства загалом і його підсистем – галузей, регіонів тощо; комплекси моделей виробництва, споживання, формування і розподілу доходів, трудових ресурсів, ціноутворення, фінансових зв’язків тощо.
Спинімося більш докладно на характеристиці таких класів економіко-математичних моделей, що мають особливості методології і техніки моделювання.
Відповідно до загальної класифікації математичних моделей вони поділяються на функціональні та структурні, а також проміжні форми (структурно-функціональні). У дослідженнях на народногосподарському рівні частіше застосовуються структурні моделі, оскільки для планування та управління велике значення мають внутрішні залежності між елементами систем. Типовими структурними моделями є моделі міжгалузевих зв’язків. Функціональні моделі широко застосовуються в економічному регулюванні, коли на поведінку об’єкта ("вихід") впливають шляхом зміни "входу". Прикладом може слугувати модель поведінки споживачів в умовах товарно-грошових відносин. Один і той самий об’єкт може описуватись одночасно і структурною, і функціональною моделями. Наприклад, для планування окремої галузевої системи використовується структурна модель, а на народногосподарському рівні кожна галузь може бути подана функціональною моделлю.
Моделі поділяють на дескриптивні та нормативні. Дескриптивні моделі відповідають на запитання: як це відбувається чи як це найімовірніше може розвиватися далі? Іншими словами, вони лише пояснюють факти, які спостерігалися, чи дають прогноз. Нормативні моделі відповідають на запитання: як це має бути? Тобто передбачають цілеспрямовану діяльність. Типовим прикладом нормативних моделей є моделі оптимального (раціонального) планування, що формалізують у той чи інший спосіб мету економічного розвитку, можливість і засоби її досягнення.
Застосування дескриптивного підходу в моделюванні економіки пояснюється необхідністю емпіричного виявлення суттєвих залежностей в економіці, встановлення статистичних закономірностей економічної поведінки соціальних груп, вивчення ймовірних шляхів розвитку якихось процесів за незмінних умов чи таких, що відбуваються без зовнішніх впливів. Прикладом дескриптивних моделей є виробничі функції та функції купівельного попиту, побудовані на підставі опрацювання статистичних даних.
Чи є економіко-математична модель дескриптивною або нормативною – це залежить не лише від її математичної структури, а й від характеру використання моделі. Наприклад, модель міжгалузевого балансу є дескриптивною, якщо вона використовується для аналізу пропорцій минулого періоду. Але ця сама математична модель стає нормативною, якщо застосовується для розрахунків збалансованих варіантів розвитку народного господарства, які задовольняють кінцеві потреби суспільства за умови планових нормативів виробничих витрат.
Багато економіко-математичних моделей поєднують ознаки дескриптивних і нормативних моделей. Типовою є ситуація, коли нормативна модель складної структури об’єднує окремі блоки, котрі є частковими дескриптивними моделями. Наприклад, міжгалузева модель може включати функції купівельного попиту, які описують поведінку споживачів за зміни доходів. Подібні приклади характеризують тенденцію ефективного поєднання дескриптивного і нормативного підходів. Дескриптивний підхід широко застосовується в імітаційному моделюванні.
За характером відображення причинно-наслідкових аспектів розрізняють моделі жорстко детерміновані і моделі, що враховують випадковість і невизначеність. Треба розрізняти невизначеність, яка описується ймовірнісними законами, і невизначеність, для опису котрої закони теорії ймовірностей застосовувати не можна. Другий тип невизначеності набагато складніший для моделювання: мається на увазі теорія нечітких множин та нечітка логіка.
За способами відображення чинника часу економіко-математичні моделі поділяються на статичні й динамічні. У статичних моделях усі залежності відносять до одного моменту чи періоду часу. Динамічні моделі характеризують зміни економічних процесів у часі. За тривалістю розглянутого періоду розрізняють моделі короткотермінового (до року), середньотермінового (до 5 років), довготермінового (10–15 і більше років) прогнозування і планування. Час в економіко-математичних моделях може змінюватися неперервно або дискретно.
Моделі економічних процесів надзвичайно різноманітні за формою математичних залежностей. Важливо виокремити клас лінійних моделей, що набули великого поширення завдяки зручності їх використання. Відмінності між лінійними і нелінійними моделями є суттєвими не лише з математичної точки зору, а й у теоретико-економічному відношенні, бо багато залежностей в економіці мають принципово нелінійний характер: ефективність використання ресурсів за зростання виробництва, зміни попиту і споживання населення, збільшення виробництва, зміни попиту населення зі зростанням доходів тощо. Теорія "лінійної економіки" істотно відрізняється від теорії "нелінійної економіки". Від того, чи вважаються множини виробничих потужностей підсистем (галузей, підприємств) опуклими чи неопуклими, суттєво залежать висновки про можливість поєднання централізованого планування й господарської самостійності економічних підсистем.
За співвідношенням екзогенних і ендогенних змінних, які включаються в модель, вони поділяються на відкриті і закриті. Повністю відкритих моделей не існує; модель повинна містити хоча б одну ендогенну (таку, що визначається за допомогою моделі) змінну. Повністю закриті економіко-математичні моделі, тобто такі, що не містять екзогенних змінних, надзвичайно рідкісні; побудова їх потребує повного абстрагування від "середовища", тобто серйозного огрублення економічних систем, які завжди мають зовнішні зв’язки. Переважна більшість економіко-математичних моделей посідає проміжну позицію і розрізняється за ступенем відкритості (закритості).
Для моделей народногосподарського рівня важливим є поділ на агреговані та деталізовані. Залежно від того, містять народногосподарські моделі просторові чинники й умови чи не містять, розрізняють моделі просторові і точкові.
Зазначимо, що під математичним моделюванням мається на увазі також процес установлення відповідності для деякої даної реальної системи S з деякою, що відповідає наведеним вище вимогам, математичною моделлю М і дослідження цієї моделі (М), що дозволяє отримати як характеристики, так і оцінки поведінки реальної системи в певних інтервалах значень її показників і параметрів.
Класифікація видів математичних моделей може проводитися й за такими ознаками: аналітичне та комп’ютерне моделювання (рис. 1).
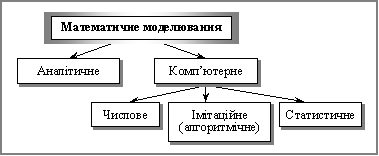
Рис. 1. Аналітичне та комп’ютерне моделювання
Для аналітичного моделювання характерним є те, що процеси функціонування елементів системи записують у вигляді деяких математичних співвідношень (алгебраїчних, інтегро-диференційних, кінцево-різницевих тощо) чи логічних умов.
Аналітична модель може досліджуватися такими методами:
а) аналітичним, коли прагнуть у загальному вигляді отримати деякі залежності для шуканих характеристик;
б) числовим;
в) якісним, коли, не маючи явного розв’язку, все ж знаходять деякі властивості рішень.
Комп’ютерне моделювання характеризується тим, що математична модель системи (використовуючи основні співвідношення аналітичного моделювання, – на цьому необхідно зробити наголос) подається у вигляді деякого алгоритму та програми, придатної для її реалізації на комп’ютері, що дозволяє проводити з нею обчислювальні експерименти. Залежно від математичного інструментарію (апарату), що використовується в побудові моделі, та способу організації обчислювальних експериментів можна виокремити три взаємопов’язані види моделювання: числове, алгоритмічне (імітаційне) та статистичне.
За числового моделювання для побудови комп’ютерної моделі використовуються методи обчислювальної математики, а обчислювальний експеримент полягає в числовому розв’язанні деяких математичних рівнянь за заданих значень параметрів і початкових умов.
Алгоритмічне (імітаційне) моделювання (може бути як детермінованим, так і стохастичним) – це вид комп’ютерного моделювання, для якого характерним є відтворення на комп’ютері (імітація) процесу функціонування досліджуваної складної системи. Тут імітуються (з використанням аналітичних залежностей і моделей) елементарні явища, що становлять процес, зі збереженням їхньої логічної та семантичної структури, послідовності плину в часі, що дозволяє отримати нову інформацію про стан системи S у задані моменти часу.
Статистичне моделювання – це вид комп’ютерного моделювання, який дозволяє отримати статистичні дані відносно процесів у модельованій системі S.
Зазначимо, що все частіше (і це логічно) в економіці використовується комбіноване моделювання, системотвірним елементом якого є аналітичні моделі.
У побудові та використанні комбінованих моделей попередньо проводять декомпозицію процесу функціонування моделі на складові елементи.
З розвитком економіко-математичних досліджень ускладнюється й проблема класифікації моделей, що використовуються. Разом із виникненням нових типів моделей (особливо змішаних типів) і нових ознак їх класифікації здійснюється процес інтеграції моделей різних типів у більш складні модельні конструкції.
Основні етапи процесу моделювання розглядалися вище. Зауважимо, що в різних галузях знань, зокрема в економіці, вони набувають специфічних рис. Проаналізуймо послідовність і зміст етапів одного циклу економіко-математичного моделювання.
1. Постановка економічної проблеми та її якісний аналіз. Головне тут – чітко сформулювати сутність проблеми (цілі дослідження), припущення, які приймаються, і ті питання, на які необхідно одержати відповіді. Цей етап включає виокремлення найважливіших рис і властивостей об’єкта, що моделюється, і абстрагування від другорядних; вивчення структури об’єкта і головних залежностей, що поєднують його елементи; формулювання гіпотез (хоча б попередніх), що пояснюють поведінку і розвиток об’єкта.
2. Побудова математичних моделей. Це – етап формалізації економічної проблеми, вираження її у вигляді конкретних математичних залежностей і відношень (функцій, рівнянь, нерівностей тощо). Спочатку зазвичай визначається основна конструкція (тип) математичної моделі, а потім уточнюються деталі цієї конструкції (конкретний перелік змінних і параметрів, форма зв’язків). Таким чином, побудова моделі має кілька стадій. Неправильно думати, що чим більше чинників ураховує модель, тим краще вона "працює" і ліпші дає результати. Те саме можна сказати й про такі характеристики складності моделі, як використовувані форми математичних залежностей (лінійні та нелінійні), урахування чинників випадковості й невизначеності тощо. Надмірна складність і деталізованість моделі утруднює процес дослідження. Треба не лише враховувати реальні можливості інформаційного і математичного забезпечення, а й порівнювати витрати на моделювання з одержуваним ефектом (зі зростанням складності моделі приріст витрат може перевищити приріст ефекту). Однією з важливих особливостей математичних моделей є потенційна можливість їх використання для вирішення різноманітних проблем. Тому, навіть зустрічаючись з новою економічною задачею, не треба намагатися "винаходити" модель; спочатку необхідно спробувати застосувати для розв’язання цієї задачі вже відомі моделі (адаптувати їх до задачі).
У процесі побудови моделі здійснюється зіставлення двох систем наукових знань – економічних і математичних. Звичайно, треба прагнути того, щоб одержати модель, яка належить до добре вивченого класу математичних задач. Часто це вдається зробити шляхом деякого спрощення вихідних положень моделі, які не спотворюють суттєві риси модельованого об’єкта. Однак можлива й така ситуація, коли формалізація економічної проблеми приводить до невідомої раніше математичної структури. Проблеми економічної науки і практики в середині ХХ ст. сприяли розвиткові математичного програмування, теорії гри, функціонального аналізу, обчислювальної математики. Цілком імовірно, що в майбутньому розвиток економічної науки стане важливим стимулом для створення нових розділів математики.
3. Математичний аналіз моделі. Метою цього етапу є з’ясування загальних властивостей моделі. Тут часто застосовують математичні прийоми дослідження. Найважливіший момент – доведення існування рішень у сформованій моделі (теорема існування). Якщо поталанить довести, що математична задача не має рішення, то необхідність у наступній роботі за первісним варіантом моделі відпадає; слід скоригувати чи постановку економічної задачі, чи модифікувати її математичну формалізацію. В аналітичному дослідженні моделі можуть постати такі питання, як, наприклад: чи взагалі є та чи єдине рішення; які змінні (невідомі) можуть входити у рішення; які будуть співвідношення між ними; в яких межах і залежно від яких вихідних умов вони змінюються; якими є тенденції цих змін тощо. Аналітичне дослідження моделі порівняно з емпіричним (числовим) має ту перевагу, що одержувані висновки зберігають свою силу за різноманітних конкретних значень зовнішніх і внутрішніх параметрів моделі. Знання загальних властивостей моделі має настільки велике значення, що часто задля доведення подібних властивостей дослідники свідомо йдуть на ідеалізацію первинної моделі. І все-таки моделі складних економічних об’єктів з великими труднощами піддаються аналітичному дослідженню. У тих випадках, коли аналітичними методами не вдається з’ясувати загальні властивості моделі, а спрощення моделі спричиняється до недопустимих (неадекватних) результатів, переходять до числових методів дослідження.
4. Підготовка вихідної інформації. Моделювання висуває жорсткі вимоги до системи інформації. Водночас реальні можливості одержання інформації обмежують вибір моделей, які пропонуються до практичного використання. Разом з тим береться до уваги не лише принципова можливість підготовки інформації (за певний період), але й витрати на підготовку відповідних інформаційних масивів. Ці витрати не повинні перевищувати ефект від використання додаткової інформації.
У процесі підготовки інформації широко використовуються методи теорії ймовірностей, теоретичної і математичної статистики. У статистичному економіко-математичному моделюванні результуюча інформація, використовувана в одних моделях, є вихідною для функціонування інших моделей.
5. Числові розв’язки. Цей етап включає розробку алгоритмів для числового розв’язування задачі, складання програм на ЕОМ і безпосереднє проведення розрахунків. Труднощі цього етапу зумовлені передусім великою розмірністю економічних задач, необхідністю опрацювання значних масивів інформації. Звичайно розрахунки на підставі використання економіко-математичної моделі мають багатоваріантний характер. Завдяки високій швидкодії сучасних ЕОМ вдається проводити числові "модельні" експерименти, вивчаючи "поведінку" моделі при різних значеннях деяких умов. Дослідження, які проводяться за допомогою числових методів, можуть стати суттєвим доповненням до результатів аналітичного дослідження. Зазначимо, що клас економічних задач, які можна розв’язувати числовими методами, значно ширший, ніж клас задач, доступних аналітичному дослідженню.
6. Аналіз числових результатів та їх використання. На цьому, завершальному, етапі циклу виникає питання про правильність і повноту результатів моделювання, про рівень практичного застосування останніх.
Математичні методи перевірки можуть виявляти некоректність підходу до побудови моделі і тим самим звужувати клас потенційно правильних моделей. Неформальний аналіз теоретичних висновків і числових результатів, які одержують за допомогою моделі, зіставлення їх із знаннями, якими володіємо, і фактами дійсності також дозволять знаходити недоліки постановки економічної задачі, сконструйованої математичної моделі, її інформаційного і математичного забезпечення.
Взаємозв’язки етапів. Звернімо увагу на зворотні зв’язки етапів, які виникають унаслідок того, що в процесі дослідження виявляються недоліки попередніх етапів моделювання.
Уже на етапі побудови моделі може з’ясуватися, що постановка задачі суперечлива і призводить до надто складної математичної моделі. Відповідно до цього постановка економіко-математичної задачі коригується. Подальший математичний аналіз моделі (етап 3) може показати, що невелика модифікація постановки задачі чи її формалізації дає корисний аналітичний результат.
Найчастіше необхідність повернення до попередніх етапів моделювання виникає під час підготовки вихідної інформації (етап 4). Може виявитися, що необхідна інформація відсутня чи затрати на її підготовку занадто великі. Тоді доводиться повертатися до постановки задачі та її формалізації, змінюючи їх так, щоб пристосуватися до наявної інформації.
Оскільки економіко-математичні задачі можуть бути складними за своєю структурою, мати велику розмірність, то часто трапляється, що відомі алгоритми і програми для комп’ютерів не дозволяють розв’язати задачу у первісному вигляді. Якщо неможливо за короткий термін розробити нові алгоритми і програми, то вихідну постановку задачі та відповідну модель спрощують: знімають і об’єднують умови, кількість чинників, нелінійні співвідношення замінюють лінійними тощо.
Недоліки, які не вдається виправити на проміжних етапах моделювання, усуваються в наступних циклах. Але результати кожного циклу мають і цілком самостійне значення. Почавши дослідження від побудови простої моделі, можна швидко одержати корисні результати, а потім перейти до створення більш досконалої моделі, яка доповнюється новими умовами, котрі включають уточнені математичні залежності.
З розвитком і ускладненням економіко-математичного моделювання деякі його етапи виокремлюються у спеціалізовані сфери дослідження, підсилюються відмінності між теоретико-аналітичними і прикладними моделями, відбувається диференціація моделей за рівнями абстракції та ідеалізації.
Теорія математичного аналізу математичних моделей економіки розвинулась в особливу гілку сучасної науки – математичну економіку. Моделі, які вивчаються в межах математичної економіки, часто втрачають безпосередній зв’язок з економічною реальністю; вони мають справу з виключно ідеалізованими економічними об’єктами та ситуаціями. У побудові таких моделей головним принципом є не стільки наближення до реальності, скільки одержання якомога більшої кількості аналітичних ресурсів за допомогою аналітичних доведень. Цінність цих моделей для економічної теорії і практики полягає у тому, що вони слугують теоретичною базою для моделей прикладного типу.
Досить самостійними царинами дослідження стають підготовка й опрацювання економічної інформації та розробка математичного забезпечення економічних задач (створення баз даних і банків інформації, програм автоматизованої побудови моделей і програмного сервісу для економістів-користувачів). На етапі практичного використання моделей провідну роль мають відігравати фахівці у відповідній галузі економічного аналізу, планування, управління. Головною ділянкою роботи системних аналітиків залишається постановка та формалізація економічних задач і синтез процесу економіко-математичного моделювання.
Список літератури
1. fingal.com.ua/content/view/888/39/1/0
2. Вітлінський В.В. Моделювання економіки: Навч. посібник. – К.: КНЕУ, 2003. – 408 с.
Похожие работы
... ічного університету, доктором технічних наук, професором М-П.Зборщиком. Висновок установи, в якій виконано дисертацію, с першою і дуже важливою її експертизою з точки зору відповідності дисертації вимогам “Порядку”. Висновок затверджується ректором (директором) або проректором (заступником директора) з наукової роботи, які несуть персональну відповідальність за якість, об'єктивність і строки пі ...
... всіма, чия робота безпосередньо пов’язана зі здійсненням валютних операцій. СПИСОК ОСНОВНИХ ПРАЦЬ ЗА ТЕМОЮ ДИСЕРТАЦІЇ 1. Козловський С.В. Прогнозування валютного курсу в Україні на основі нечіткої логіки // Вісник ВПІ. - 2007. - № 3 (42). - С.39-49. 2. Козловський С.В. Застосування новітніх методів моделювання стану валютного ринку України // Вісник Тернопільської академії народного ...
... в тексті подвійний варіант він / вона, зрештою, це може дратувати. Таким чином, краще обминати займенникові форми, щоб нікого не образити й дотримуватися офіційного стилю. Не прикрашають науковий текст і неточності, розмиті визначення, захоплення епітетами „надзвичайний”, „неймовірний”, „катастрофічний”, „добрий”, „гарний”, „рідкий”, „значний” і т.д. Виразність викладу, чіткість передачі і ...
... ін одним з перших став попереджати про можливу екологічну кризу. Він довів, що історичний розвиток людства пов’язаний із регіональними відмінностями територій і, навпаки, по мірі ускладнення соціально-економічної структури суспільства географічний фактор його розвитку збільшує свій вплив (наприклад, зростає залежність економіки від природних ресурсів через збільшення обсягів їх використання). Дію ...
0 комментариев