Навигация
Корпорація М(1) = 0,6*9,5+0,4*(-2) = 4,9 млн. грн.;
1 корпорація М(1) = 0,6*9,5+0,4*(-2) = 4,9 млн. грн.;
2 корпорація М(2) = 0,7*13,5+0,3*(-2) = 8,85 млн. грн.;
створення асоціації М(А) = 0,3*26,5+0,7*(-2,5) = 6,2 млн. грн.
Отже, входження до другої корпорації має найбільше очікуване значення прибутку.
Обчислимо для кожного варіанту злиття показники варіації прибутку фірми: дисперсію, середньоквадратичне відхилення та коефіцієнт варіації.
1) входження до першої корпорації:
дисперсія D(1) = 0,6*(9,5–4,9)2+0,4*(-2–4,9)2 = 31,74;
середньоквадратичне відхилення ![]() млн. грн.;
млн. грн.;
коефіцієнт варіації ![]() .
.
2) входження до другої корпорації:
дисперсія D(2) = 0,7*(13,5–8,85)2+0,3*(-2–8,85)2 = 50,4525;
середньоквадратичне відхилення ![]() млн. грн.;
млн. грн.;
коефіцієнт варіації ![]() .
.
3) створення асоціації:
дисперсія D(А) = 0,3*(26,5–6,2)2+0,7*(-2,5–6,2)2 = 176,61;
середньоквадратичне відхилення ![]() млн. грн.;
млн. грн.;
коефіцієнт варіації ![]() .
.
Коефіцієнту варіації має такий зміст: це величина ризику відхилень, що припадає на одиницю очікуваного прибутку.
Отже, найменший ризик у абсолютному вимірі (середньоквадратичне відхилення) має входження у першу корпорацію. Але у відносному вимірі (коефіцієнт варіації) найменший ризик має входження до другої корпорації. Враховуючи, що крім цього входження до другої корпорації має найбільше очікуване значення прибутку, то слід обрати варіант входження до другої корпорації.
Завдання 3Підприємство має 12 філій, розташованих в різних районах області. Керівництво має дослідити, яким чином впливають торгівельна площа, середньоденна інтенсивність потоку покупців та середньоденний дохід на річний товарообіг філії. Статистичні дані наведені в таблиці:
| № філії | Річний товарообіг, млн. грн. | Торгівельна площа, тис. м2 | Середньоденна інтенсивність потоку покупців, тис. чол. /день | Середньоденний дохід, тис. грн. |
| У | Х1 | Х2 | Х3 | |
| 1 | 3,08 | 0,37 | 10,54 | 5,495 |
| 2 | 5,42 | 1,04 | 7,81 | 5,625 |
| 3 | 7 | 1,27 | 11,11 | 6,775 |
| 4 | 7,16 | 1,35 | 10,19 | 6,305 |
| 5 | 7,17 | 1,18 | 14,02 | 9,975 |
| 6 | 8,5 | 1,55 | 14,22 | 8,775 |
| 7 | 4,48 | 0,84 | 8,84 | 5,525 |
| 8 | 5,92 | 1 | 12,66 | 7,755 |
| 9 | 7,83 | 1,35 | 12,57 | 7,875 |
| 10 | 3,31 | 0,54 | 11,31 | 6,275 |
| 11 | 1,67 | 0,3 | 8,55 | 5,235 |
| 12 | 3,3 | 0,61 | 9,61 | 5,325 |
Обчислити парні коефіцієнти кореляції та дослідити модель на мультиколінеарність. Якщо є залежні фактори, виключити один з них (довести, чому саме цей фактор вилучено).
Побудувати діаграми розсіювання для припущення щодо вигляду залежності між показником та факторами, що залишилися в моделі. Обчислити оцінки параметрів множинної регресії. Дати інтерпретацію оцінок параметрів.
Визначити коефіцієнти кореляції, детермінації, оцінений коефіцієнт детермінації. Дати пояснення щодо отриманих результатів.
З надійністю 0,95 за допомогою критерію Фішера оцінити адекватність прийнятої математичної моделі статистичним даним та за допомогою критерію Стьюдента оцінити значимість параметрів регресії. Пояснити отримані результати.
Визначити частинні коефіцієнти еластичності та пояснити їх сенс.
Розв’язання:
Використаємо критерій ![]() для перевірки моделі на мультиколінеарність. Для цього нормалізуємо змінні
для перевірки моделі на мультиколінеарність. Для цього нормалізуємо змінні ![]() економетричної моделі за формулою
економетричної моделі за формулою
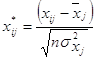 ,
,
де ![]() – кількість спостережень, (
– кількість спостережень, (![]() );
);
![]() – кількість незалежних змінних, (
– кількість незалежних змінних, (![]() );
);
![]() – середня арифметична
– середня арифметична ![]() -ї незалежної змінної;
-ї незалежної змінної;
![]() – дисперсія
– дисперсія ![]() -ї незалежної змінної.
-ї незалежної змінної.
Результати нормалізації змінних ![]() ,
, ![]() ,
, ![]() подамо в таблиці:
подамо в таблиці:
|
|
|
|
|
|
|
|
| 1 | 0,45 | 10,94 | 5,995 | -0,4207 | -0,0593 | -0,2458 |
| 2 | 1,12 | 8,21 | 6,125 | 0,0653 | -0,4515 | -0,2202 |
| 3 | 1,35 | 11,51 | 7,275 | 0,2321 | 0,0226 | 0,0059 |
| 4 | 1,43 | 10,59 | 6,805 | 0,2901 | -0,1096 | -0,0865 |
| 5 | 1,26 | 14,42 | 10,475 | 0,1668 | 0,4408 | 0,6351 |
| 6 | 1,63 | 14,62 | 9,275 | 0,4352 | 0,4695 | 0,3991 |
| 7 | 0,92 | 9,24 | 6,025 | -0,0798 | -0,3035 | -0,2399 |
| 8 | 1,08 | 13,06 | 8,255 | 0,0363 | 0,2453 | 0,1986 |
| 9 | 1,43 | 12,97 | 8,375 | 0,2901 | 0,2324 | 0,2222 |
| 10 | 0,62 | 11,71 | 6,775 | -0,2974 | 0,0514 | -0,0924 |
| 11 | 0,38 | 8,95 | 5,735 | -0,4715 | -0,3452 | -0,2969 |
| 12 | 0,69 | 10,01 | 5,825 | -0,2466 | -0,1929 | -0,2792 |
Побудуємо нову ![]() -матрицю, елементами якої є нормалізовані змінні
-матрицю, елементами якої є нормалізовані змінні ![]() , і обчислимо кореляційну матрицю:
, і обчислимо кореляційну матрицю:
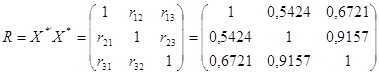 ,
,
де ![]() – матриця, транспонована до матриці
– матриця, транспонована до матриці ![]() (елементи матриці
(елементи матриці ![]() характеризують щільність зв’язку між двома незалежними змінними; (
характеризують щільність зв’язку між двома незалежними змінними; (![]() ) – парні коефіцієнти кореляції). Аналізуючи значення цих коефіцієнтів, робимо припущення, що між змінними
) – парні коефіцієнти кореляції). Аналізуючи значення цих коефіцієнтів, робимо припущення, що між змінними ![]() і
і ![]() існує сильний зв’язок.
існує сильний зв’язок.
Знайдемо визначник кореляційної матриці ![]() :
: ![]() ; потім визначимо критерій
; потім визначимо критерій ![]() :
:
![]() .
.
Для ![]() ступенів свободи і рівня значущості
ступенів свободи і рівня значущості ![]() табличне значення критерію
табличне значення критерію ![]() . Оскільки обчислене значення більше за табличне, то в моделі присутня мультиколінеарність.
. Оскільки обчислене значення більше за табличне, то в моделі присутня мультиколінеарність.
Складемо розрахункову таблицю для обчислення коефіцієнтів кореляції між факторами і показником:
| № | Y | X2 | X3 | Y2 | X22 | X32 | YX2 | YX3 |
| 1 | 3,08 | 10,54 | 5,495 | 9,4864 | 111,0916 | 30,19503 | 32,4632 | 16,9246 |
| 2 | 5,42 | 7,81 | 5,625 | 29,3764 | 60,9961 | 31,64063 | 42,3302 | 30,4875 |
| 3 | 7 | 11,11 | 6,775 | 49 | 123,4321 | 45,90063 | 77,77 | 47,425 |
| 4 | 7,16 | 10,19 | 6,305 | 51,2656 | 103,8361 | 39,75303 | 72,9604 | 45,1438 |
| 5 | 7,17 | 14,02 | 9,975 | 51,4089 | 196,5604 | 99,50063 | 100,5234 | 71,52075 |
| 6 | 8,5 | 14,22 | 8,775 | 72,25 | 202,2084 | 77,00063 | 120,87 | 74,5875 |
| 7 | 4,48 | 8,84 | 5,525 | 20,0704 | 78,1456 | 30,52563 | 39,6032 | 24,752 |
| 8 | 5,92 | 12,66 | 7,755 | 35,0464 | 160,2756 | 60,14003 | 74,9472 | 45,9096 |
| 9 | 7,83 | 12,57 | 7,875 | 61,3089 | 158,0049 | 62,01563 | 98,4231 | 61,66125 |
| 10 | 3,31 | 11,31 | 6,275 | 10,9561 | 127,9161 | 39,37563 | 37,4361 | 20,77025 |
| 11 | 1,67 | 8,55 | 5,235 | 2,7889 | 73,1025 | 27,40523 | 14,2785 | 8,74245 |
| 12 | 3,3 | 9,61 | 5,325 | 10,89 | 92,3521 | 28,35563 | 31,713 | 17,5725 |
| Сума | 64,84 | 131,43 | 80,94 | 403,848 | 1487,922 | 571,8083 | 743,3183 | 465,4972 |
| Середнє | 5,4033 | 10,9525 | 6,7450 | 33,6540 | 123,9935 | 47,6507 | 61,9432 | 38,7914 |
Обчислимо коефіцієнти кореляції:
![]() ;
;

Відповідно до обчислених коефіцієнтів кореляції, показник Y має тісніший зв’язок із змінною Х3 порівняно із змінною Х2. Тому відкинемо фактор Х2. Будемо розглядати модель Y=Y(X1, X3).
Для припущення про вигляд залежності побудуємо діаграми розсіювання між показником та факторами, що залишилися в моделі.
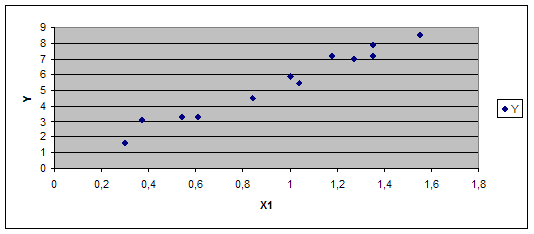
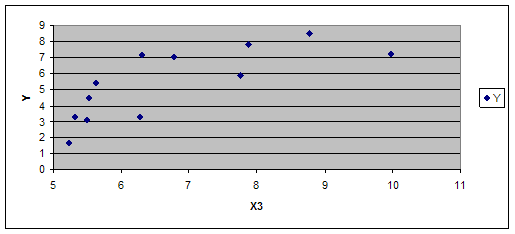
Обчислимо оцінки параметрів множинної регресії у лінійній формі:
![]() .
.
Відповідно до методу найменших квадратів (МНК) оператор оцінювання параметрів моделі має вигляд
![]() ,
,
де 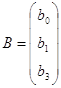 ;
; ![]() – матриця, транспонована до матриці
– матриця, транспонована до матриці ![]() . Матриця
. Матриця ![]() , крім двох векторів змінних Х1 та Х3, містить вектор одиниць. Згідно з оператором оцінювання одержимо:
, крім двох векторів змінних Х1 та Х3, містить вектор одиниць. Згідно з оператором оцінювання одержимо:
1) 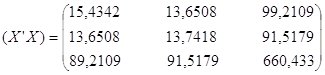 ;
;
2) 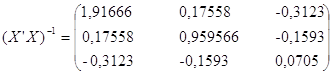 ;
;
3) 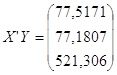 ;
;
4) 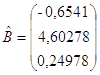 .
.
Отже, отримали таку модель лінійної множинної регресії:
![]() .
.
Оцінки параметрів моделі мають такий економічний зміст:
1) ![]() : якщо за інших рівних умов змінна Х1 збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшується (зменшується) на 4,60278. Конкретно це означає, що збільшення (зменшення) торгової площі на 1 тис. м2 приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 4,60278 млн. грн.;
: якщо за інших рівних умов змінна Х1 збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшується (зменшується) на 4,60278. Конкретно це означає, що збільшення (зменшення) торгової площі на 1 тис. м2 приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 4,60278 млн. грн.;
2) ![]() : якщо за інших рівних умов змінна Х3 збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшиться (зменшиться) на 0,24978. Конкретно це означає, що збільшення (зменшення) середньоденного доходу на 1 тис. грн. приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 0,24978 млн. грн.
: якщо за інших рівних умов змінна Х3 збільшиться (зменшиться) на одиницю, то відповідно до цієї оцінки змінна Y збільшиться (зменшиться) на 0,24978. Конкретно це означає, що збільшення (зменшення) середньоденного доходу на 1 тис. грн. приведе, за інших рівних умов, до збільшення (зменшення) річного товарообігу цієї філії на 0,24978 млн. грн.
Обчислимо суми квадратів:
![]() .
.
Визначимо коефіцієнт детермінації
![]() ,
,
оцінений коефіцієнт детермінації
![]() ,
,
коефіцієнт множинної кореляції
![]() .
.
Оскільки отримані значення є близькими до одиниці, то можна зробити висновок про тісний зв’язок між річним товарообігом і незалежними змінними. При цьому понад 98% варіації річного товарообігу пояснюється варіацією торгівельної площі та середньоденного доходу.
Обчислимо критерій Фішера
![]() .
.
Критичне значення критерію Фішера при рівні значущості ![]() і кількості ступенів свободи
і кількості ступенів свободи ![]() та
та ![]() дорівнює
дорівнює ![]() . Порівнюючи обчислене значення критерію Фішера з критичним, робимо висновок про адекватність прийнятої математичної моделі статистичним даним.
. Порівнюючи обчислене значення критерію Фішера з критичним, робимо висновок про адекватність прийнятої математичної моделі статистичним даним.
Матриця ![]() є матрицею коваріацій оцінок параметрів моделі. Діагональні елементи
є матрицею коваріацій оцінок параметрів моделі. Діагональні елементи ![]() цієї матриці використаємо для обчислення стандартних похибок параметрів моделі.
цієї матриці використаємо для обчислення стандартних похибок параметрів моделі.
Знайдемо дисперсію залишків за формулою ![]() . Таким чином,
. Таким чином, ![]() . Визначимо стандартні похибки оцінок параметрів моделі, використовуючи дисперсію залишків:
. Визначимо стандартні похибки оцінок параметрів моделі, використовуючи дисперсію залишків:
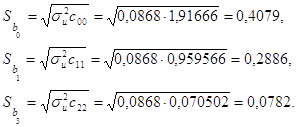
Обчислимо значення ![]() -критеріїв:
-критеріїв:
![]() ;
; ![]() ;
;  .
.
Табличне значення ![]() -критерію при
-критерію при ![]() ступенях свободи і рівні значущості α = 0,05 становить 2,262. Всі фактичні значення
ступенях свободи і рівні значущості α = 0,05 становить 2,262. Всі фактичні значення ![]() -критеріїв, окрім критерію для вільного члена, перевищують за модулем табличне значення. Отже, статистично значущими є всі параметри моделі, крім вільного члена.
-критеріїв, окрім критерію для вільного члена, перевищують за модулем табличне значення. Отже, статистично значущими є всі параметри моделі, крім вільного члена.
Визначимо коефіцієнти еластичності за формулами
![]() ,
, ![]() ,
,
де f(X) = -0,6541 + 4,60278 X1 + 0,24978 X3. – рівняння регресії, знайдене вище:
![]() ;
;
![]() .
.
Отримані коефіцієнти еластичності показують, на скільки% у середньому змінюється показник Y стосовно своєї величини при зміні відповідного фактора на 1% від свого середнього значення.
Список літератури
1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. шк., 1986.
2. Машина Н.І. Економічний ризик і методи його вимірювання. Навчальний посібник. – К: ЦУЛ, 2003. –188 с.
3. Толбатов Ю.А. Економетрика: Підручник для студентів економічних спеціальностей вищих навчальних закладів. – К.: Четверта хвиля, 1997 – 320 с.
Похожие работы
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
... прийняти міри по недопущенню подальшого погіршення фінансового стану та обрати заходи по більш раціональному управлінню капіталом підприємства з ціллю підвищення ефективності фінансово-економічної діяльності. 2. ПІДВИЩЕННЯ ЕФЕКТИВНОСТІ ДІЯЛЬНОСТІ ПІДПРИЄМСТВА ТОВ „ПОЛІПРОМІНВЕСТ” 2.1 Рекомендації та заходи з поліпшення ефективності фінансово-економічної діяльності підприємства ТОВ «Поліпром ...
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
... праць. За матеріалами міжнародної науково-практичної конференції, Київ, 27-28 березня 2007 року. - К.: КНЕУ. - 2007. С.371-372. - 0,1 друк. арк. АНОТАЦІЯ Сільченко М.В. Економіко-математичне моделювання процесу ціноутворення на ринку опціонів. - Рукопис. Дисертація на здобуття наукового ступеня кандидата економічних наук за спеціальністю 08.03.08 - економіко-математичне моделювання. - Киї ...

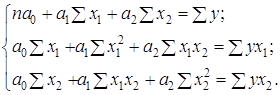
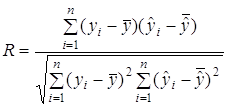
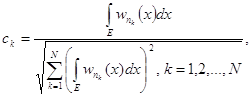
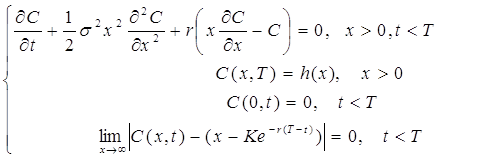
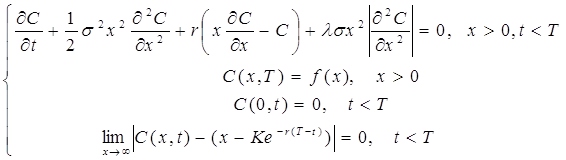
0 комментариев