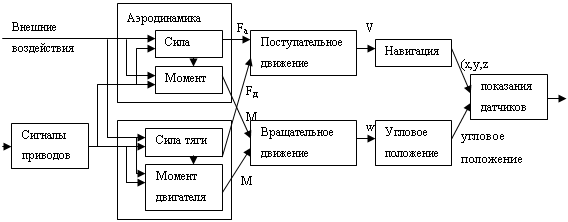
Навигация
Министерство общего и профессионального образования РФ
Кафедра «Системы управления»
КУРСОВАЯ РАБОТА ПО ИССЛЕДОВАНИЮ ОПЕРАЦИЙВариант 14
Челябинск, 2004
Содержание
1. Задача 1
2. Задача 2
3. Задача 3
4. Задача 4
Приложение
1. Задача 1
Условие:
Нефтеперерабатывающий завод получает 4 полуфабриката: x1 тыс. л. алкилата, x2 тыс. л. крекинг-бензина, x3 тыс. л. бензина прямой перегонки и x4 тыс. л. изопентана. В результате смешивания этих четырех компонентов в разных пропорциях образуется три сорта авиационного бензина: бензин А (а1:а2:а3:а4), бензин В (b1:b2:b3:b4) и бензин С (с1:с2:с3:с4).
Стоимость 1 тыс. л. бензина каждого сорта равна y1 руб., y2 руб. и y3 руб.
Определить соотношение компонентов, при котором будет достигнута максимальная стоимость всей продукции.
| № вар. | x1 | x2 | x3 | x4 | y1 | y2 | y3 | а1 | а2 | а3 | а4 | b1 | b2 |
| 1 | 400 | 250 | 350 | 100 | 120 | 100 | 150 | 2 | 3 | 5 | 2 | 3 | 1 |
| № вар. | b1 | b2 | c1 | c2 | c3 | c4 |
| 1 | 2 | 1 | 2 | 2 | 1 | 3 |
Решение:
Составим математическую модель задачи.
Обозначим через t1 количество бензина А;
через t2 количество бензина В;
через t3 количество бензина С.
Тогда, целевая функция будет
L=y1t1+ y2t2+ y3t3=120t1+100t2+150t3 →max
Система ограничений:
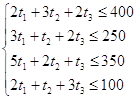
Приведем систему ограничений к виду основной задачи линейного программирования (введем новые переменные t4 , t5 ,t6 ,t7, которые входят в целевую функцию с нулевыми коэффициентами):
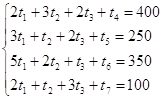
Выберем t1 , t2 ,t3 свободными переменными, а t4 , t5 ,t6 ,t7 – базисными и приведем к стандартному виду для решения с помощью симплекс-таблицы:
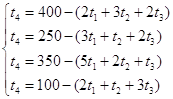
L=0-(-120t1-100t2-150t3)
Составим симплекс-таблицу.
Это решение опорное, т.к. все свободные члены положительны.
Т. к. все коэффициенты в целевой функции отрицательные, то можно взять любой столбец разрешающим (пусть t1). Выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это t7)
| b | t1 | t2 | t3 | ||||||
| L | 0 | -120 | -100 | -150 | |||||
| 6000 | 60 | 60 | 180 | ||||||
| t4 | 400 | 2 | 3 | 2 | 400/2=200 | ||||
| -100 | -1 | -1 | -3 | ||||||
| t5 | 250 | 3 | 1 | 2 | 250/3=83,3 | ||||
| -150 | -1,5 | -1,5 | -4,5 | ||||||
| t6 | 350 | 5 | 2 | 1 | 350/5=70 | ||||
| -250 | -2,5 | -2,5 | -7,5 | ||||||
| t7 | 100 | 2 | 1 | 3 | 100/2=50 | ||||
| 50 | 0,5 | 0,5 | 1,5 | ||||||
Далее меняем t2 и t1 .
| b | t7 | t2 | t3 | ||||||
| L | 6000 | 60 | -40 | 30 | |||||
| 4000 | 40 | 80 | 120 | ||||||
| t4 | 300 | -1 | 2 | -1 | 300/2=150 | ||||
| -200 | -2 | -4 | -6 | ||||||
| t5 | 100 | -1,5 | -0,5 | -2,5 | |||||
| 50 | 0,5 | 1 | -4,5 | ||||||
| t6 | 50 | -2,5 | -0,5 | -6,5 | |||||
| 50 | 0,5 | 1 | -7,5 | ||||||
| t1 | 50 | 0,5 | 0,5 | 1,5 | 50/0,5=100 | ||||
| 100 | 1 | 2 | 1,5 | ||||||
| b | t7 | t1 | t3 | |||||
| L | 10000 | 100 | 80 | 150 | ||||
| t4 | 100 | -3 | -4 | -7 | ||||
| t5 | 150 | -1 | 1 | -1 | ||||
| t6 | 100 | -2 | 1 | -5 | ||||
| t2 | 100 | 1 | 2 | 3 | ||||
Т.к. коэффициенты при переменных в целевой функции положительны, следовательно, это оптимальное решение.
Таким образом, t1 = t3 =0; t2=100; L=10000.
Т.е. для получения максимальной прибыли следует производить только бензин В (100 тыс. л.), при этом выручка составит 10000 руб.
ОТВЕТ: для получения максимальной прибыли следует производить только бензин В (100 тыс. л.), при этом выручка составит 10000 руб.
Похожие работы
... , 6) сетевого планирования и управления, 7) выбора маршрута, 8) комбинированные. Из перечисленных выше методов математического программирования наиболее развитым и законченным является линейное программирование. В его рамки укладывается широкий круг задач исследования операций. Линейное программирование Несмотря на требование линейности целевой функции и ограничений, в рамки линейного ...
... -бухгалтер должен: а) потребовать недостающие материалы у проверяемой организации; б) составить сообщение о невозможности дачи заключения; в) заявить письменное ходатайство о предоставлении ему дополнительных документов. 1. Исследование операций по заработной плате Задачей судебно-бухгалтерской экспертизы при исследовании операций по труду и заработной плате является активизация ...
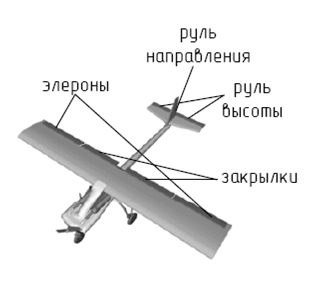
... и направление ветра, плотность воздуха и др. 4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю. Исследование операций Задача 1 Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она ...
... Лагранжа: L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13). Получим уравнения седловой точки, применяя теорему Куна-Таккера: i=1;2 Объединим неравенства в систему А, а равенства в систему В: Система А: Система В: Перепишем систему А: 6-4x1-4x2+2,5u1+3u2 <0 1,5-4x1-2x2-u1+2,5u2 <0 2,5x1-x2–7³0 3x1+2,5x2–13³0 4)Введем новые ...
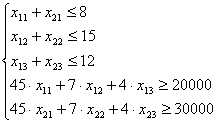
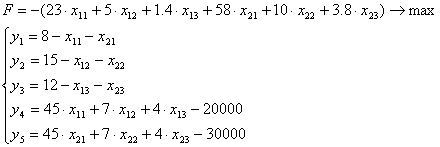
0 комментариев