Навигация
Исследование операций и теория систем
Министерство Образования Российской Федерации
Южно-Уральский Государственный Университет
Кафедра Системы Управления
КУРСОВАЯ РАБОТА
по дисциплине: Исследование операций
Вариант 8
Руководитель:
Плотникова Н.В.
«___»__________2004 г.
Автор проекта:
студентка группы
ПС – 317
Куликова Мария
«___»__________2004 г.
Проект защищен
с оценкой
«___»__________2004 г.
Челябинск
2004 г.
Содержание.
Задача 1………………………………………………………………….3
Задача 2………………………………………………………………….8
Задача 3…………………………………………………………………10
Задача 4…………………………………………………………………13
Задача 1 (№8)
Условие:
На производстве четырёх видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км. кабеля данного вида на каждой из групп операций, прибыль от реализации 1 км. каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, указаны в таблице.
Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной.
| Технологическая операция | Нормы затрат времени на обработку 1 км кабеля вида | Общий фонд рабочего времени (ч) | |||
| 1 | 2 | 3 | 4 | ||
| Волочение | а11 | а12 | а13 | а14 | А1 |
| Наложение изоляций | а21 | а22 | а23 | а24 | А2 |
| Скручивание элементов в кабель | а31 | а32 | а33 | а34 | А3 |
| Освинцовывание | а41 | а42 | а43 | а44 | А4 |
| Испытание и контроль | а51 | а52 | а53 | а54 | А5 |
| Прибыль от реализации 1 км кабеля | В1 | В2 | В3 | В4 | |
| №вар. | а11 | а12 | а13 | а14 | а21 | а22 | а23 | а24 | а31 | а32 | а33 | а34 | а41 |
| 1 | 1,5 | 1 | 2 | 1 | 1 | 2 | 0 | 2 | 4 | 5 | 5 | 4 | 2 |
| № вар. | а42 | а43 | а44 | а51 | а52 | а53 | а54 | А1 | А2 | А3 | А4 | 5 |
| 1 | 1 | 4 | 0 | 1 | 2 | 1,5 | 4 | 6500 | 4000 | 11000 | 4500 | 4500 |
| В1 | В2 | В3 | В4 |
| 1 | 2 | 1,5 | 1 |
Решение:
Составляем математическую модель задачи:
пусть x1 –длина 1-ого кабеля (км);
x2 – длина 2-ого кабеля (км);
x3 – длина 3-ого кабеля (км);
x4 – длина 4-ого кабеля (км)
тогда целевая функция L - общая прибыль от реализации изготовляемой продукции, будет иметь следующий вид
L= В1x1 + В2x2 + В3x3 + В4x4 = x1+ 2x2 + 1,5x3 + x4 → max
Получим систему ограничений:
1,5x1 + x2 + 2x3+ x4 £ 6500;
x1 + 2x2 + 0x3+2x4 £ 4000;
4x1 + 5x2 + 5x3+4x4 £11000;
2x1 + x2 +1,5x3+0x4 £ 4500;
x1 + 2x2 +1,5x3+4x4 £ 4500.
Приведём полученную математическую модель к виду ОЗЛП с помощью добавочных неотрицательных переменных, число которых равно числу неравенств:
1,5x1 + x2 + 2x3+ x4 + x5 = 6500;
x1 + 2x2 + 0x3+2x4 + x6= 4000;
4x1 + 5x2 + 5x3+4x4 + x7=11000;
2x1 + x2 +1,5x3+0x4 + x8 =4500;
x1 + 2x2 +1,5x3+4x4 + x9 =4500.
Итак, выберем x1, x2, x3, x4 - свободными переменными, а x5, x6, x7, x8, x9 - базисными переменными (каждая из них встречаются в системе лишь в одном уравнении с коэффициентом 1, а в остальных с нулевыми коэффициентами). Приведём систему к стандартному виду, выразив для этого все базисные переменные через свободные:
x5 = 6500 – (1,5x1 + x2 + 2x3+ x4 );
x6 = 4000 – ( x1 + 2x2 + 0x3+2x4);
x7 =11000 - ( 4x1 + 5x2 + 5x3+4x4);
x8 =4500 – ( 2x1 + x2 +1,5x3+0x4);
x9 =4500 – ( x1 + 2x2 +1,5x3+4x4)
L=0 –(- x1- 2x2 - 1,5x3 - x4)
Решим методом симплекс-таблиц:
Это решение опорное, т.к. все свободные члены положительны.
Выберем столбец в таблице, который будет разрешающим, пусть это будет x1, выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это x8).
| A |
|
|
|
| |
| L | 0 2250 | -1 0,5 | -2 0,5 | -1,5 2 | -1 0 |
|
| 6500 -3375 | 1,5 -0,75 | 1 -0,75 | 2 -3 | 1 0 |
|
| 4000 -2250 | 1 -0,5 | 2 -0,5 | 0 -2 | 3 0 |
|
| 11000 -9000 | 4 -2 | 5 -2 | 5 -8 | 4 0 |
| x8 | 4500 2250 | 2 0,5 | 1 0,5 | 4 2 | 0 0 |
| x9 | 4500 -2250 | 1 -0,5 | 2 -0,5 | 1,5 -2 | 4 0 |
Меняем ![]() и
и ![]()
| A | x8 |
|
|
| |
| L | 2250 1000 | 0,5 -1 | -1,5 0,5 | 0,5 -1,5 | -1 2 |
|
| 3125 -500/3 | -0,75 1/6 | 0,25 -1/12 | -1 0,25 | 1 -1/3 |
|
| 1750 -1000 | -0,5 1 | 1,5 -0,5 | -2 1,5 | 3 -2 |
|
| 2000 2000/3 | -2 -2/3 | 3 1/3 | -3 -1 | 4 4/3 |
|
| 2250 -1000/3 | 0,5 1/3 | 0,5 -1/6 | 2 0,5 | 0 -2/3 |
| x9 | 2250 -1000 | -0,5 1 | 1,5 -0,5 | -0,5 1,5 | 4 -2 |
Меняем ![]() и x9
и x9
| A | x8 |
|
|
| |
| L | 3250 250 | -0,5 0,5 | 0,5 -0,5 | -1 1 | 1 2 |
|
| 8875/3 187,5 | -7/12 0,375 | -1/12 -0,375 | -0,75 0,75 | 2/3 1,5 |
|
| 750 125 | 0,5 0,25 | -0,5 -0,25 | -0,5 0,5 | 1 1 |
|
| 2000/3 250 | -2/3 0,5 | 1/3 -0,5 | -1 1 | 4/3 2 |
|
| 5750/3 -625 | 5/6 -1,25 | -1/6 1,25 | 2,5 -2,5 | -2/3 -5 |
| x9 | 250 250 | 0,5 0,5 | -0,5 -0,5 | 1 1 | 2 2 |
| A | x8 |
| x9 |
| |
| L | 3500 | 0 | 0 | 1 | 3 |
|
| 18875/6 | -5/24 | -11/24 | 0,75 | 13/6 |
|
| 875 | 0,75 | -0,75 | 0,5 | 2 |
|
| 2750/3 | -1/6 | -1/6 | 1 | 10/3 |
|
| 3875/3 | -5/12 | 13/12 | -2,5 | -17/3 |
|
| 250 | 0,5 | -0,5 | 1 | 2 |
Видим, что коэффициенты при переменных в целевой функции положительны, значит, найденное решение будет оптимальным.
Итак, ![]() =0,
=0, ![]() =3875/3,
=3875/3, ![]() =2750/3,
=2750/3, ![]() =250, L=3500.
=250, L=3500.
Ответ: если предприятие будет изготавливать только три вида проволоки 1,2,3 причем 3875/3 км, 2750/3 км, 250 км соответственно, то общая прибыль от реализации изготовляемой продукции будет максимальной и равной 3500(ед).
Задача 2 (№28)
Условие:
С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции Q=CTx при условии Ax ³ £B,
где CT = [ c1 c2 . . . c6 ]T , ВT = [ b1 b2 . . . b6 ]T ,
XT = [ x1 x2 . . . x6]T , А= [aij] (i=1,6; j=1,3).
| № вар. | с1 | с2 | с3 | с4 | с5 | с6 | b1 | b2 | b3 | Знаки ограничений | a11 | a12 | a13 | a14 | |||
| 1 | 2 | 3 | |||||||||||||||
| 28 | -6 | 0 | 1 | -1 | -1 | 0 | 8 | 2 | 3 | = | = | = | 4 | 1 | 1 | 2 | |
| № вар. | a15 | a16 | a21 | a22 | a23 | a24 | a25 | a26 | a31 | a32 | a33 | a34 | a35 | a36 | Тип экстрем. |
| 1. 34 | 1 | 0 | 2 | -1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | max |
Решение:
Получим систему:
Похожие работы
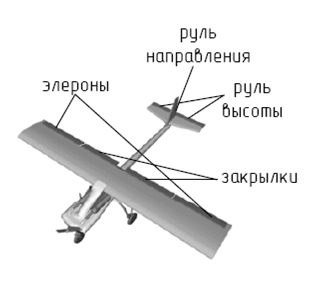
... и направление ветра, плотность воздуха и др. 4. Эквифинальность. Рано или поздно, самолет вынужден будет приземлится или разобьется. Т.о. скорости, ускорения, моменты и силы будут равны нулю. Исследование операций Задача 1 Авиакомпания «Небесный грузовик», обслуживающая периферийные районы страны, располагает А1 самолетами типа 1, А2 самолетами типа 2, А3 самолетами типа 3, которые она ...
... называют системообразующие, системоохраняющие факторы, важными среди которых являются неоднородность и противоречивость ее элементов. Коммуникативность. Эта закономерность составляет основу определения системы, предложенного В. Н. Садовским и Э. Г, Юдиным в книге «Исследования по общей теории систем». Система образует особое единство со средой; как правило, любая исследуемая система представляет ...
... буржуа. М. 1987. Гвардини Р. Конец Нового времени//"Вопросы философии", 1990. Легенда о докторе Фаусте. М. 1978. I. АНТРОПОЛОГИЧЕСКАЯ ТРАДИЦИЯ В КУЛЬТУРОЛОГИИ 1. КУЛЬТУРОЛОГИЯ - ИНТЕГРАЦИЯ ЗНАНИЙ О КУЛЬТУРЕ Антропологическая традиция в культурологии — традиция исследования культуры в культурной и социальной антропологии. Культурология как интегративная наука формируется на стыке целого ряда ...
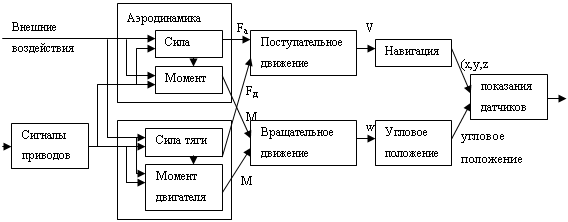
... damn(t)/dt =[daij(t)/dt] 1.3 ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА. Физический объект - физическое устройство, характеризуемое некоторым числом свойств, соответствующих целям его использования. В теории систем существенным является не физическое, а математическое описание свойств объекта и соотношений между ними. В теории систем объектом А является абстрактный объект, связанный с множеством ...
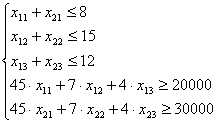
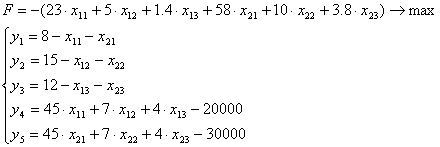
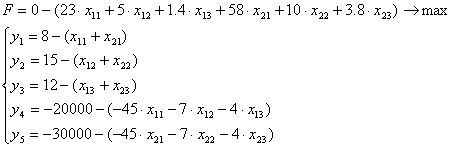




0 комментариев