Навигация
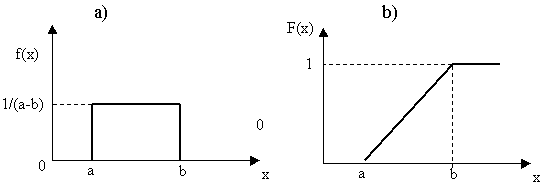
Построение гистограммы распределения
3. Построение гистограммы распределения.
4.Вычисление статист. по критерию Х² Пирсона.
5.Проверка гипотезы о равномерном распределении чисел от 0,1,2,..g, полученных генератором случайных чисел.
Таблица1
Критические точки распределения
| Число степеней свободы r | Уровень значимости ά | |||||
| 0.01 | 0.025 | 0.05 | 0.95 | 0.975 | 0.99 | |
| 1 | 6.6 | 5.0 | 3.8 | 0.0039 | 0.00089 | 0.00016 |
| 2 | 9.2 | 7,4 | 6,0 | 0,103 | 0.051 | 0.20 |
| 3 | 11.3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 |
| 4 | 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 |
| 5 | 15,1 | 12,8 | 11,1 | 0,115 | 0,831 | 0,554 |
| 6 | 16,8 | 14,4 | 12,6 | 0,164 | 1,24 | 0,872 |
| 7 | 18,5 | 16,0 | 14,1 | 0,217 | 1,69 | 1,24 |
| 8 | 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 |
| 9 | 21,7 | 19,0 | 16,9 | 3,33 | 2,70 | 2,09 |
| 10 | 23,2 | 20,5 | 18,3 | 3,94 | 3,21 | 2,56 |
| 11 | 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 |
| 12 | 26,2 | 23,3 | 20,0 | 5,23 | 4,40 | 3,57 |
| 13 | 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 |
| 14 | 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 |
| 15 | 30,6 | 27,5 | 25,0 | 7,26 | 6,26 | 5,23 |
| 16 | 32,0 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 |
| 17 | 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 |
| 18 | 34,8 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 |
| 19 | 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 |
| 20 | 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 |
| 21 | 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,90 |
| 22 | 40,3 | 36,8 | 33,9 | 12,3 | 11,0 | 9,54 |
| 23 | 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 |
| 24 | 43,0 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 |
| 25 | 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 |
| 26 | 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 |
| 27 | 47,0 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 |
| 28 | 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 |
| 29 | 49,6 | 45,7 | 42,6 | 17,7 | 16,02 | 14,3 |
| 30 | 50,9 | 47,0 | 43,8 | 18,5 | 16,8 | 15,0 |
Таблица 2
Варианты заданий к лабораторной работе
| q | m | n | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
| 1 | 3 | 3 | 5 | 0 | 1 | 2 | 1 | 1 | - | - |
| 2 | 2 | 3 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 3 | 2 | 5 | 7 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 4 | 3 | 2 | 5 | 1 | 1 | 1 | 1 | 1 | - | - |
| 5 | 2 | 4 | 7 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 6 | 3 | 3 | 5 | 0 | 0 | 0 | 1 | 1 | - | - |
| 7 | 3 | 3 | 6 | 0 | 1 | 2 | 1 | 2 | 0 | - |
| 8 | 3 | 4 | 6 | 1 | 1 | 1 | 2 | 2 | 2 | - |
| 9 | 3 | 5 | 6 | 1 | 1 | 1 | 0 | 0 | 2 | - |
| 10 | 2 | 3 | 7 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 11 | 2 | 6 | 7 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 12 | 2 | 2 | 7 | 0 | 1 | 0 | 1 | 0 | 2 | 0 |
| 13 | 3 | 3 | 5 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 14 | 2 | 2 | 6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 15 | 3 | 4 | 5 | 1 | 2 | 1 | 0 | 1 | 2 | 2 |
Интерфейс программы
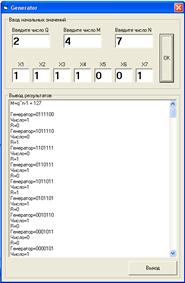
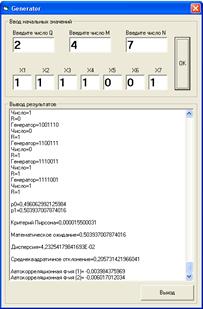
Введённые значения: q-2, M-4, N-7
X1-1, X2-1, X3-1, X4-1, X5-0, X6-0, X7-1
Листинг программы
Public m, n, q, r, xe As Integer
Private Sub Command2_Click()
End
End Sub
Private Sub ok_Click()
list.Clear
If tm.Text = "" Or tn.Text = "" Or tq.Text = "" Or tx(0).Text = "" Or tx(1).Text = "" Or tx(2).Text = "" Or tx(3).Text = "" Or tx(4).Text = "" Then
MsgBox ("Сначала введите все значения")
Exit Sub
Else
Call fun
End If
End Sub
Private Sub fun()
Dim reg, regt As String
Dim xi(6), yi(100000), p(2), p0, p1, p2 As Integer
Dim xe As Double
n = CInt(tn.Text)
m = CInt(tm.Text)
q = CInt(tq.Text)
For i = 0 To (n - 1)
reg = reg & CStr(tx(i).Text)
Next
mg = q ^ n - 1
list.AddItem ("M=q^n-1 = " & mg)
list.AddItem ("")
For i = 1 To mg
yi(i) = Right(reg, 1)
r = CInt(Mid(reg, m, 1)) + CInt(Right(reg, 1))
If r >= q Then
r = r - q
Else
End If
If r = 0 Then p0 = p0 + 1
If r = 1 Then p1 = p1 + 1
If r = 2 Then p2 = p2 + 1
regt = reg
reg = CStr(r) & Mid(regt, 1, (n - 1))
list.AddItem ("Генератор=" & reg)
list.AddItem ("Число=" & yi(i))
list.AddItem ("R=" & r)
Next
list.AddItem ("")
p(0) = p0 / mg
p(1) = p1 / mg
p(2) = p2 / mg
For w = 0 To q - 1
list.AddItem ("p" & w & "=" & p(w))
Next w
For j = 0 To q - 1
xe = xe + ((1 / q) - p(j)) ^ 2
Next
xe = (1 / q) * xe
list.AddItem ("")
list.AddItem ("Критерий Пирсона=" & Round(xe, 12))
Dim mx, dx, kr, k As Double
mx = 0
For j = 1 To mg
mx = mx + CInt(yi(j))
Next
mx = mx / mg
list.AddItem ("")
list.AddItem ("Математическое ожидание=" & mx)
For j = 1 To mg
dx = (CInt(yi(i)) - mx) ^ 2
Next
dx = dx / (n - 1)
list.AddItem ("")
list.AddItem ("Дисперсия=" & dx)
list.AddItem ("")
list.AddItem ("Среднеквадратичное отклонение=" & Sqr(dx))
list.AddItem ("")
For i = 1 To q
For j = 1 To (mg - i)
k = k + ((CInt(yi(j)) - mx) * (CInt(yi(j + i)) - mx))
Next
kr = k / (mg - i - 1)
list.AddItem ("Автокорреляционная ф-ия (" & i & ")= " & Round(kr, 12))
Next
End Sub
Список используемой литературы
1. Ли И. Т., Лабораторный практикум. Имитационное моделирование экономических процессов, Душанбе 2008 год
Похожие работы
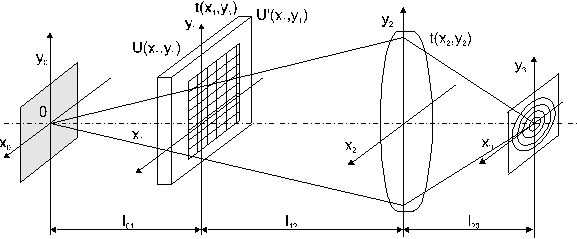
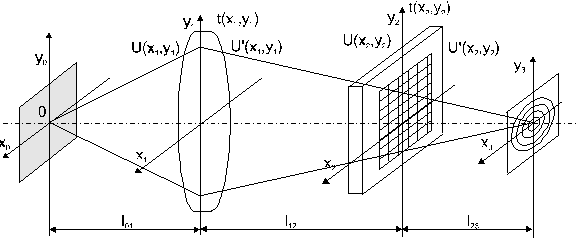
... -ным законом распределения ширины щелей и стенок может быть представ-лен следующим выражением: (2.16). Наибольший интерес для практической реализации в оптических системах КОС для автоматизации контроля статистических характеристик пространственной структуры ЛЗ представляет второе слагаемое выражения (2.16), содержащее функциональную взаимосвязь этих характеристик. Пос-кольку это слагаемое ...
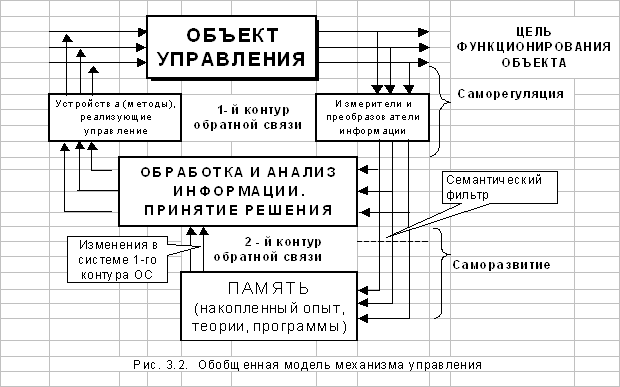
... Возникшие потребности в научно обоснованных методах и средствах управления нашли свое выражение в кибернетике - науке об управлении и системном анализе, особым предметом исследования которых являются сложные и очень сложные системы окружающего мира. 4.4 Организационные системы Традиционно современная кибернетика рассматривала, в основном, простые и сложные управляемые системы, для которых ...
... на ЭВМ, колеблется в достаточно широких пределах в зависимости от класса объекта моделирования, вида оцениваемых характеристик, необходимой точности и достоверности результатов моделирования. Для метода статистического моделирования на ЭВМ характерно, что большое число операций, а соответственно большая доля машинного времени расходуются на действия со случайными числами. Кроме того, результаты ...
... итерационного процесса, состоящего из последовательно реализуемых шагов, удовлетворяющих направлению: s → 0, Cpk -> Ср. 4. ИСПОЛЬЗОВАНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ АНАЛИЗА ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ Рассмотрим применение вышеизложенных статистических методов контроля качества производственных процессов на нескольких примерах. 4.1 Контроль технологической точности Пример 4.1.1. ...
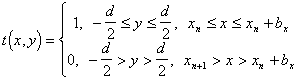



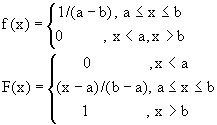
0 комментариев