Навигация
Зв’язок арифметичного матеріалу з геометричним
3. Зв’язок арифметичного матеріалу з геометричним
„Арифметика надає геометрії різноманітні послуги, дістаючи, у свою чергу, від цієї науки різноманітні імпульси” - так говорив німецький математик XIX ст. Л.Кронекер.
Продуктивне використання ідеї „арифметика допомагає геометрії” (і навпаки) сягає сивої давнини. Так, 2,5 тис. років тому грецький мудрець Фалес Мілетський (близько 624-548 рр. до н.е.) за допомогою тіні визначив висоту однієї з єгипетських пірамід.
У народі кажуть: „Що людина бачить, те вона і знає”. Нині графіки, діаграми, схеми, графи досить поширені в різних галузях науки і виробництва. Не випадково, мабуть, і в самому шкільному курсі вони використовуються дедалі частіше.
У підручниках математики для чотирирічної початкової школи (автор - М.В. Богданович, Л.П. Кочина, М.М. Левшин) вміщено в середньому близько 5% вправ, де різноманітні схематичні малюнки допомагають дітям виконати суто арифметичні завдання. Вони ілюструють правила, хід міркувань, умову вправи чи задачі; за ними учні складають і розв’язують приклади (рівняння, нерівності) і задачі, пояснюють, як знайшли результат дій, називають правильні твердження, читають вирази тощо.
Схематичний малюнок виконує різнопланові дидактичні функції:
- допомагає осмислити сюжет, виявити подані величини та взаємозв’язки між ними;
- „наштовхує” на здогадку про можливий початок розв’язання, допомагає збагнути його спосіб, обґрунтувати правомірність чи раціональність;
- слугує підготовчою вправою до введення правил виконання чотирьох арифметичних дій, запису різних обчислювальних алгоритмів у вигляді блок-схем;
- виступає як спосіб розв’язання задач та їх перевірки, засіб і джерело нових арифметичних знань та інше.
Розглянемо, як геометрія допомагає арифметиці, зокрема, спинимось на застосуванні графічних і графіко-обчислювальних прийомів розв’язування арифметичних задач.
Обчислювальні прийоми розв’язування задач інколи корисно замінити графічними, застосувавши схематичні малюнки. Вони або відразу приводять до потрібного результату, або значно полегшують пошук способу розв’язання; арифметичного - спрямовуючи міркування в потрібне русло, чи алгебраїчного - допомагаючи у виборі невідомого для складання рівняння.
Найбільше підходять для графічного розв’язання задач відрізки і прямокутники, оскільки на множині відрізків прямої, як і на множині прямокутників з рівними основами, визначені операції додавання і множення на невід’ємне число, тобто операції, схожі на арифметичні дії додавання і множення невід’ємних чисел.
Що ж до методики опрацювання задач у такий спосіб, то тут важливо урізноманітнювати переходи від умови до схеми, від схеми до числового виразу, а від нього знову до умови; частково змінювати схему: числовий вираз або умову з тим, щоб глибше з’ясувати залежності між величинами, відображеними в умовах.
Графічне моделювання математичного змісту задачі допомагає побачити, яких саме даних не вистачає (або які зайві). З’ясувавши потрібну залежність, легко знайти шуканий результат.
Нарешті, правильно побудовані графічні моделі умов задач у багатьох випадках дають змогу учням зробити „прикидку” очікуваної відповіді, а також перевірити правильність арифметичного розв’язання задачі.
Один з видів творчої роботи над задачею - розв’язування їх різними методами - арифметичним, алгебраїчним, геометричним. Інколи графічне розв’язання найбільш наочне, раціональне, обґрунтоване.
Часто та сама задача має кілька розв’язань. Тоді кажуть про різні способи її розв’язування.
Значну частину арифметичних вправ корисно розв’язати з учнями за допомогою різних схем, діаграм, графіків тощо: вони дедалі більше проникають у шкільну математику.
Отже, ми бачимо, що арифметика і геометрія перебувають у тісному взаємозв’язку і без цього неможлива робота на уроках математики в початкових класах.
Висновки
Часто доводиться чути нарікання, що в молодших класах учень вчився на відмінно, а в середніх „з’їхав” на трійки.
Перебуваючи на переддипломній практиці, я хотіла знайти відповідь на питання: чому виходить саме так?
І мені здається, це можна пояснити насамперед тим, що, формуючи знання, уміння і навички, класоводи передусім прагнули розвинути пам’ять дитини і менше уваги приділяли іншим важливим компонентам пізнавальної сфери, таким, як відчуття, сприймання, мислення. Тим часом, лише за умови їх гармонійного розвитку школярі успішно опановують прийомами, узагальнені способи дій, що становлять зміст навчальної діяльності.
На мою думку, більшість учителів формує у дітей просторові уявлення в курсі математики, складовою якого є геометрія. Однак з практики видно, що результат такої роботи як у початковій, так і в середній ланці та старших класах, залишають бажати кращого. Тим часом у численних дослідженнях педагогів уже не раз підтверджувалась необхідність і доцільність підготовки учнів до вивчення геометрії, а відтак - і розробки додаткового, пропедевтичного курсу для 1-4 - х класів.
Проведена мною робота дала змогу дійти висновку, що розвитку просторових уявлень молодших школярів сприяють дидактичні комп’ютерні ігри. На них передусім і зосереджується увага заслужених вчителів. Ними підбираються різні комп’ютерні ігрові програми: „Дивовижний квадрат”, „Викладання квадратів”, „Складені многокутники”, „Чарівне коло” та інші. Саме на цих іграх учні легко засвоюють графічні оператори побудови крапки, лінії, прямокутника, кола; вчаться створювати з фігур різні композиції. Молодші школярі погано розбираються в кольоровій гамі, та робота на комп’ютері (розфарбовування різних фігур) допомагає усунути й цей недолік.
Під час своєї переддипломної практики я звертала велику увагу на те, як ще вчителі формують основні знання дітей з геометрії. І я побачила, що майже весь геометричний матеріал подається дітям на основі вже їхніх знань, хоча ці знання ще зовсім маленькі. Але саме таким шляхом відбувається краще засвоєння у дітей найпотрібніших геометричних понять.
І на мою думку, це вірний шлях, тому що всім нам відомо, що краще запам’ятовується те, до чого сам додумався.
Література
1. Бантова М.О. Методика викладання математики в початкових класах. Методика вивчення геометричного матеріалу. К.: Вища школа, 1982.
2. Гора Т.П. Формування в учнів графічних навичок. //Початкова школа, 1986, № 5.
3. Гришко А.Г. Формування поняття про геометричні фігури. //Початкова школа, 1988, № 4.
4. Друзь Б.Г. Геометрія допомагає арифметиці. //Початкова школа, 1991, №4.
5. Друзь Б.Г. Геометрія допомагає арифметиці. //Початкова школа, 1991, № 6.
6. Дудко О.М. Викладання пропедевтичного курсу геометрії в початкових класах. //Початкова школа, 1991, № 11.
7. Кухар В.М. Український національний костюм на уроках математики. //Початкова школа, 1995, № 5.
ДОДАТКИ
Додаток 1
Формування поняття про геометричні фігури
За програмою з математики вже у 1 класі (ще до вивчення чисел першого десятка) вводиться поняття геометричної фігури. В цей час увага дітей зосереджується на властивостях предметів, розміщення їх на площині і в просторі, дається поняття про величину тощо, тому цілком природно вичленити геометричну форму. До того ж зробити це нескладно, бо школярі оперують достатньою кількістю різноманітних наочних посібників, дидактичним матеріалом. Наведемо приклади.
Заняття 1
Подорож у країну Геометрію
Учитель заздалегідь малює на дошці кольоровою крейдою різноманітні геометричні фігури (трикутник, прямокутник, квадрат, круг, точку, відрізок і т.п.), або виставляє на фланелографі їх кольорові макети, чи вивішує відповідну таблицю. Поки що все закрите шторкою.
- Діти! Зараз ми з вами вирушимо у цікаву подорож до країни Геометрії (відкриває шторку, учні розглядають, пізнають окремі фігури). Знайомтеся! Зображене тут - жителі цієї країни, тому й називаються геометричними фігурами. Ми їх вивчатимемо. Дізнаємося багато цікавого про них: чим схожі і чим різняться, як їх будувати. Отже, вивчатимемо геометрію - науку про властивості різних фігур.
Слово „геометрія” - грецьке, у перекладі на нашу мову означає „землемірство”. Така назва виникла тому, що геометричні знання використовувалися в давнину для вимірювання на місцевості (землі). А сьогодні такі знання потрібні кожному: водієві і художнику, механізатору і космонавту, кравчині і будівельнику. Тому геометрію вивчають усі.
Потім класовод пропонує дітям назвати відомі фігури, запам’ятати назви нових, учить порівнювати. Наприкінці заняття учні „роблять фотознімки чарівним апаратом”, і геометричні фігури назавжди залишаються на таблиці у класі.
Заняття 2
Найважливіша фігура
- Уявімо, що наша класна дошка - віконечко у незвичайний дім Геометрії. В ньому мешкають цікаві предмети, які оживають тільки в руках працьовитих і кмітливих дітей. Коли їх беруть у руки, вони швидко й вправно креслять, вимірюють усе вздовж і впоперек, угору й униз. Хочете подивитися в це віконечко і дізнатися, хто там живе? Давайте попросимо найголовнішу геометричну фігуру, щоб прочинила його. (Вчитель вивішує таблицю геометричних фігур}. А котра ж з них найголовніша? (Промовляє таємниче, майже пошепки).
Я - невидимка. В цьому суть моя
Мене лиш дотиком пера чи крейди зображають
І точкою усюди називають.
- То яка найголовніша фігура? Хто був уважним, той почув і головне про цю невидимку. (Точка). Покажіть її на таблиці. Як же зобразити точку? Так, треба доторкнутися кінчиком олівця чи ручки до паперу (кінчиком крейди до дошки). А чому вона найголовніша? От коли ви потоваришуєте з нею, запам’ятаєте її ім’я, вона щодня відкриватиме вам віконечко у невідоме. Як зараз. Повторіть, як називається ця фігура.
Учитель відкриває дошку. На ній прилади: учнівська лінійка, макет метра, косинець, циркуль, олівець, розсувний кут (малка), складаний метр. Учні називають відомі інструменти і їх призначення, а класовод показує, як ними користуватися, ознайомлює з рештою фігур. Від імені Точки дарує олівці, і діти із задоволенням вчаться зображати цю фігуру у зошитах.
Так по черзі до школярів на урок математики приходять фігури, прилади із стародавньої країни Геометрії, а з ними - знання і практичні навички. Найстаранніших Точка „відзначає” - від її імені вчитель при огляді учнівських робіт наклеює у зошит у зошит зображення сонця.
Для закріплення знань та відпрацювання навичок учні виконують вправи за поданим зразком - ставлять точку посередині клітинки, в лівому нижньому куті, у правому верхньому і т.д. Це підготовляє їх водночас до написання цифр, тренує кисть руки.
З позначенням геометричних фігур буквами поспішати не слід. Скориставшись аналогією до запису імен, прізвищ з великої літери, спочатку у 2 класі можна показати, що точку теж треба назвати якоюсь буквою. Для цього пропонуємо відповідні вправи - усні і письмові. Обов’язково звертаємо увагу дітей точка не має виміру, й усі фігури утворюються з точок, але при цьому виділяються „головні” - це кінці відрізка, вершина трикутника, прямокутника, центр кола.
Для ознайомлення з відрізком пропонуємо на довільній прямій позначити дві точки і повідомляємо, що частина прямої між ними називається відрізком, а самі точки - його кінцями. Відрізок позначаємо великими буквами на кінцях або малою - посередині.
Доцільно провести практичну роботу: відкласти довгий відрізок за допомогою шнура, натертого крейдою. Цим способом користуються столярі. Прикріплюють шнур на протилежних кінцях дошки, потім, тримаючи посередині, трохи його відтягують і різко відпускають. Шнур відбиває відрізок потрібної довжини.
Під час введення поняття про кут важливо запобігти виникненню в учнів неправильного уявлення, що ця фігура розміщується тільки горизонтально. Для цього показуємо дітям кути різного виду і в різному положенні: на предметах у класі, на роздатковому лічильному матеріалі тощо. Щоразу пояснюємо: в кожного кута є сторони та вершина. Коли дві суміжні сторони прямокутника (трикутника) сходяться, вони теж утворюють кут. Щоб сформувати правильне уявлення про кут як сукупність вершини, сторін і внутрішньої площини між ними, треба на перших порах оперувати паперовими, пластмасовими чи дерев’яними моделями цих фігур, а після цього варто показати розсувний кут -малку. До речі, діти можуть виготовити його самі з планочок, шарнірно з’єднаних шматочком пластиліну чи цвяхом.
У такий спосіб на різних моделях, малюнках поступово збагачуємо поняття про кут. Школярі наочно переконуються: його величина не залежить від довжини сторін, а лише від їх взаємного розміщення. Варто на розсувному куті ввести поняття про види цієї фігури - прямі, тупі й гострі. Запропонувати виготовити модель прямого кута з паперу: двічі перегнути навпіл аркуш довільної форми. Вчитель звертає увагу, що при цьому дві прямі (лінії згину), перетинаючись, утворюють чотири однакових кути. Вони і називаються прямими.
З аркушів паперу різної величини учні виготовляють багато таких кутів, а потім накладанням їх один на одного переконуються, що прямі кути рівні між собою. Користуючись моделлю цієї геометричної фігури, знаходять такі самі кути на різних предметах (менші або більші за прямі), прикладають до моделей кутів креслярський косинець і знову перевіряють їх величину. Учитель повідомляє: менші за прямий кути називаються гострими, а більші - тупими.
Для ознайомлення з прямокутником доцільно провести таку практичну роботу. Зобразивши два чотирикутники (один з них - прямокутник), запропонувати дітям відповісти на запитання, що спільного мають ці фігури, чим відрізняються одна від одної. Розглянувши їх, учні легко встановлять, що обидва - чотирикутні, а скориставшись моделлю прямого кута, з’ясують: у першої фігури всі кути різні, а в другої - прямі. Як інакше можна назвати другий чотирикутник? Якщо вихованці не зможуть відповісти, вчитель сам повідомляє: „Чотирикутник, у якого всі кути прямі, називається прямокутником’1.
Після цього - ознайомлення з ознаками прямокутника за допомогою вимірювання сторін. Учні мають переконатися, що протилежні сторони у цієї фігури рівні.
Щоб підкреслити суттєві ознаки прямокутника, класовод на дошці або фланелографі розміщує різної величини і кольору фігури й запитує, що спільного в них і чим вони відрізняються. Учні цілком спроможні дати обґрунтовану відповідь. Спільне - всі фігури прямокутники. Відрізняються матеріалом, величиною, кольором. Класовод наголошує: для геометричної фігури важливі дві перші ознаки - наявність прямих кутів та рівність протилежних сторін, а решта -матеріал, колір, величина - неістотні.
Аналогічно вводяться поняття про квадрат як окремий вид прямокутника.
З різновидами многокутників молодші школярі ознайомлюються у процесі формування поняття про число. Під час вивчення числа і цифри 3 вводимо поняття про трикутник, 4 - чотирикутник і т.д. Поступово діти переконуються, що назва многокутника залежить від кількості його елементів, наприклад, три кути - трикутник, чотири кути - чотирикутник і т.д.
Після тренувальних вправ на визначення фігур можна запропонувати складніші завдання.
Додаток 2
Український національний костюм на уроках математики
Задумаймося, що може бути спільного між вивченням українського національного костюма та уроками математики в початкових класах. Мабуть, нічого - скажете Ви. Але це тільки на перший погляд.
Як показали спостереження, використання матеріалів про український національний костюм, виготовлення його елементів на уроках математики забезпечують вирішення ряду важливих завдань, а саме:
- Якісно збагачується, урізноманітнюється програмовий матеріал. Учні охочіше розв’язують завдання про свою сім’ю, родину, своє село.
- Використовуючи на уроці математики етнографічні матеріали, ми повертаємось до життєдайного джерела народної мудрості, досвіду, народних знань, зокрема й математичних. Підводимо школяра до розуміння, що без знання математики люди не змогли б виготовити те чи інше знаряддя праці, створити елемент костюма, купити чи продати необхідну річ.
- У ході такої роботи вивчаємо історію, мову народу, звичаї, побут, усну народну творчість, формуємо естетичну культуру, виховуємо повагу до праці, бережливість, охайність.
Як же поєднати етнографічні матеріали і програмові завдання з математики? Очевидно, тут потрібні зміни в змісті предмета, доборі матеріалу до уроків, необхідна система творчих завдань, котра б спонукала учнів до незалежного мислення, оригінальних прийомів виконання вправ.
Використанню на уроках математики етнографічних матеріалів про костюм передує певна підготовча робота. Учні ознайомлюються з бойківським костюмом, який, крім спільних загальнонаціональних рис, має регіональні особливості, з процесами виготовлення його окремих елементів вдома, під час етнографічних експедицій, зустрічей з народними умільцями, на уроках народознавства. Спираємося на дібрані учнями матеріали на здобуті ними знання, їх досвід.
Використання на уроках математики в початкових класах етнографічних матеріалів про костюм потребує певної системи. Доречно виділити такі розділи, при опрацюванні програмового матеріалу яких доцільно використовувати народознавчі дані про костюм:
І. Вивчення кольорів (1 клас).
II. Просторові уявлення (1 клас).
III. Робота з групами предметів (1 клас).
IV. Вивчення ряду натуральних чисел першого десятка (1 клас).
V. Геометричний матеріал (1-4 клас).
VI. Арифметичні задачі (1-4 клас).
Вивченню геометричного матеріалу в початкових класах допоможе використання етнографічних матеріалів про український національний костюм.
Ряд елементів бойківського костюма мають правильну геометричну форму: „убрус” (головний убір) - прямокутник, хустка - квадрат, а складена навпіл - два трикутники і т.д.
Викрійки, що використовувались для виготовлення взуття, одягу, побудовані з об’єднаних в одне ціле геометричних фігур. Для бойківських вишивок домінуючим є геометричний орнамент, який розміщали на елементах одягу у вигляді прямокутних смужок.
Отже, при вивченні геометричного матеріалу пропоную виділити такі частини:
1. Робота з орнаментом.
2. Робота з викрійками окремих елементів в одягу.
1. Робота з орнаментом.
Для учнів початкових класів рекомендую фрагменти орнаментів сорочок „півок”, виконані технікою „хрестик”, „висьорків”, „ланок” виготовлених із різнокольорового бісеру технікою „силяння”. Добираємо фрагменти орнаментів, які не перевантажені додатковими деталями. Найскладніші за кольором і будовою вишивки рукавів. Тому використовуємо простіші фрагменти орнаментів „дудів” (манжетів), „обшивок” (бейок), а також фрагменти того орнаменту, який складається з окремих вишитих смужок на „півках”, деяких жіночих сорочках (див. рис. 1).
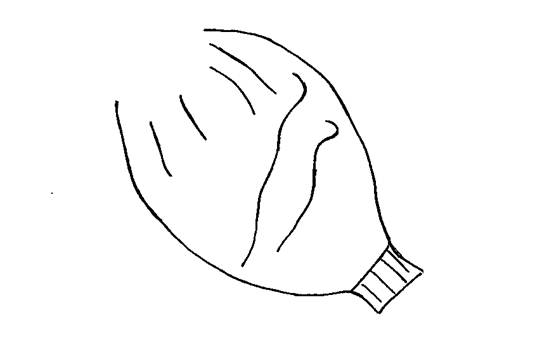
Рис.1
Відносно „ланок” і „висьорків”, ми намагаємося дібрати той фрагмент орнаменту, на якому чітко видно якусь геометричну фігуру. Як унаочнення до завдань, подаю:
а) стилізовані фрагменти орнаменту, виконані на папері в клітинку;
б) фрагменти орнаменту у вигляді кругів і хрестиків, перенесених на такий же папір;
в) побутові речі, виконані майстрами.
При використанні такого унаочнення доречно демонструвати поряд з фрагментом весь виріб або його зображення.
2. Робота з викрійками окремих елементів одягу
Кращому аналізу геометричних фігур, практичній роботі над вивченням кутів, вершин, сторін сприяє ознайомлення школярів з викрійками окремих елементів костюма, котрі мають форму геометричних фігур. Розглядаємо викрійки з полотна, для ляльки відповідних розмірів, попередньо обрублені.
Використовуємо також ілюстрації з зображенням з’єднань деталей одягу.
Виділяють такі етапи роботи:
1 етап. Аналіз викрійок з полотна як геометричних фігур.
2 етап. Показ етапів роботи з викрійками в процесі виготовлення одягу і наступний їх аналіз.
3 етап. Однаковий для всіх видів робіт з викрійками. В кінці кожного виду роботи ще раз пригадуємо зі школярами розглянути геометричні фігури, їх властивості.
Похожие работы
... . В ході нашого дослідження ми також виконали поставлені нами завдання. Вивчення психолого-педагогічних, а також і методичних аспектів використання комп’ютерних ігор у процесі навчання молодших школярів на уроках математики дало змогу проаналізувати шляхи такого використання, на основі чого створити свої. Підбір навчальних ігор для уроків математики в початковій школі дав змогу зробити певні на
... ію, інтуїцію, волю, пам'ять, вчить напружувати зусилля, керувати собою, дотримуватися правил поведінки. Розділ ІІ. Методичні основи застосування дидактичної гри на уроках математики в початковій школі 2.1 Суть дидактичної гри як методу навчання математики в початкових класах Підвищення ефективності навчального процесу обумовлено, головним чином, удосконаленням методики навчання (навчає ...
... 1. У ряді чисел 0 має стояти перед числом 1. Далі учні вчаться записувати число нуль цифрою. 1.2 Психолого-педагогічні основи використання комп’ютера при вивченні змістової лінії „Властивості та відношення предметів. Лічба” Сучасні реалії обумовлюють часткову заміну традиційних засобів навчання новими ІКТ. Використання Інтернету, різних комп'ютерних програм дозволяє одержувати різноманітну ...
... виникненням деякого задоволення, то воно й перетворюється на приємне здивування. За непродуманої ситуації може бути й навпаки: виникнути неприємне здивування. Тому важливо на початковій стадії організації позакласної роботи з математики створювати ситуації для приємного здивування. Треба враховувати, що здивування викликає у дітей більш гостру, зосереджену увагу. Здивування повинно межувати з заці ...




0 комментариев