Навигация
2.3 Описание схемы алгоритма
Алгоритмы сортировки очень сильно зависят от структуры данных.. В данной работе рассматривается сортировка массивов. Тип данных «массив» удобен тем, что хранится во внутренней памяти и имеет случайный доступ к элементам, то есть более быстрый, чем у последовательности. Поэтому массивы целесообразно использовать для хранения небольших, часто используемых множеств
Из выше сказанного следует, что в процессе работы потребуются следующие переменные:
n – количество элементов массива;
A – сортируемый массив;
j – переменная;
x – i-й ключ (переносимый элемент);
r – номер последнего обмена при просмотре входной последовательности слева-направо.
l - номер последнего обмена при просмотре входной последовательности справа -
налево.
Все переменные целого типа.
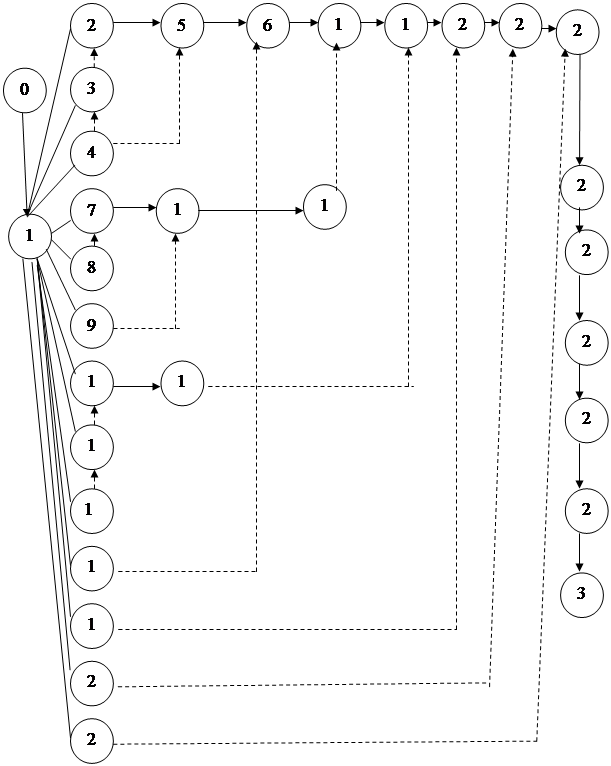
Описание схемы алгоритма. Блок-схема данного алгоритма изображена на рис. 1 в Приложении.
Алгоритм работает следующим образом. Сначала вводятся исходные данные: длина массива и его элементы (блок 1, 2) , затем организуется цикл по всей длине массива, во время которого (блоки 3 -7) и проводится сравнение элементов а[j-1]>a[j] и их обмен при проходе справа-налево . Номер последнего обмена l запоминается. Далее организуется цикл, в котором проводится проверка условия а[j-1]>a[j] при проходе массива слева-направо (блоки 8 - 12).
2.4 Контрольный пример
Рассмотрим пример работы алгоритма сортировки Шейкер.
Задан массив A, состоящий из 8 элементов: 44, 55, 12, 42, 94, 18, 6, 67.
Шаг 1. l = 2, r = 8
Таблица 2
| l | 2 | 3 | 3 | 4 | 4 |
| r | 8 | 8 | 7 | 7 | 4 |
| Направление | ↑ | ↓ | ↑ | ↓ | ↑ |
| j=1 | 44 | 6 | 6 | 6 | 6 |
| j = 2 | 55 | 44 | 44 | 12 | 12 |
| j= 3 | 12 | 55 | 12 | 44 | 18 |
| j = 4 | 42 | 12 | 42 | 18 | 42 |
| j = 5 | 94 | 42 | 55 | 42 | 44 |
| j = 6 | 18 | 94 | 18 | 55 | 55 |
| j = 7 | 6 | 18 | 67 | 67 | 67 |
| j = 8 | 67 | 67 | 94 | 94 | 94 |
1) j = r =8
2) A[7]<A[8] , j = j -1 =7
3) A[6]>A[7], x=18, A[6]=6, A[7]=x=18 ; j=6
4) A[5]>A[6], A[5] =6, A[6] = 94
5) A[4]>A[5], A[4] =6, A[5] =42
6) A[3]>A[4], A[3] =6, A[4] =12
7) A[2]>A[3], A[2] =6, A[3] = 55
8) A[1]>A[2], A[1] =6, A[2] = 44
9) l=3.
Шаг 2. A[7]<A[8] , j = j -1 =7
1) A[1]>A[2]; j=6
2) A[2]>A[3], A[1] =, A[2] = 44, j= 4
3) A[3]>A[4], A[2] =6, A[3] =12, j=5
4) A[4]>A[5], A[3] =6, A[4] =12, j=6
5) A[5]>A[6], j =7
6) A[6]>A[7], A[5] =6, A[6] = 18 , j=8
7) r =7.
Шаг 3.
1) A[7]>А[8] , j = j -1 =7
2) A[6]>A[7], x=18, A[6]=6, A[7]=x=18 ; j=6
3) A[5]>A[6], A[5] =6, A[6] = 94; j=5
4) A[4]>A[5], A[4] =6, A[5] =42; j=4
5) A[3]>A[4], A[3] =6, A[4] =12; j=3
6) A[2]>A[3], A[2] =6, A[3] = 55; j=2
7) A[1]>A[2], A[1] =6, A[2] = 44; j=1
8) l=3.
Шаг 4.
1) A[1]>A[2], x=18, A[6]=6, A[7]=x=18 ; j=6
2) A[2]>A[3], A[1] =, A[2] = 94, j= 4
3) A[3]>A[4], A[2] =6, A[3] =42, j=5
4) A[4]>A[5], A[3] =6, A[4] =12, j=6
5) A[5]>A[6], j =7
6) A[6]>A[7], A[5] =6, A[6] = 44 , j=8 ,
7) r =7. → конец алгоритма.
Таким образом, мы получили исходный массив, отсортированный методом Шейкер:
6, 12, 18, 42, 44, 55, 67, 94.
3 АЛГОРИТМ ПОКРЫТИЯ: ПОСТРОЕНИЕ ОДНОГО КРАТЧАЙШЕГО ПОКРЫТИЯ
3.1 Математическое описание задачи и методов её решения
Пусть ![]() -опорное множество. Имеется множество
-опорное множество. Имеется множество
подмножеств![]() множества B (
множества B (![]() ). Каждому подмножеству
). Каждому подмножеству![]() сопоставлено число
сопоставлено число ![]() , называемой ценой. Множество
, называемой ценой. Множество ![]() называется решением задачи о покрытии, или просто покрытием, если выполняется условие
называется решением задачи о покрытии, или просто покрытием, если выполняется условие ![]() , при этом цена
, при этом цена ![]() . Термин «покрытие» означает, что совокупность множеств
. Термин «покрытие» означает, что совокупность множеств ![]() содержит все элементы множества В, т.е. «покрывает» множество B
содержит все элементы множества В, т.е. «покрывает» множество B
Безизбыточным называется покрытие, если при удалении из него хотя бы одного элемента оно перестает быть покрытием. Иначе - покрытие избыточно.
Покрытие Р называется минимальным, если его цене ![]() - наименьшая среди всех покрытий данной задачи.
- наименьшая среди всех покрытий данной задачи.
Покрытие Р называется кратчайшим, если l - наименьшее среди всех покрытий данной задачи.
Удобным и наглядным представлением исходных данных и их преобразований в задаче о покрытии является таблица покрытий. Таблица покрытий - это матрица Т отношения принадлежности элементов множеств ![]() опорному множеству В. Столбцы матрицы сопоставлены элементам множества В, строки - элементам множества
опорному множеству В. Столбцы матрицы сопоставлены элементам множества В, строки - элементам множества
А: 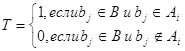
Нули в матрице T не проставляются.
Имеются следующие варианты формулировки задачи о покрытии:
Похожие работы
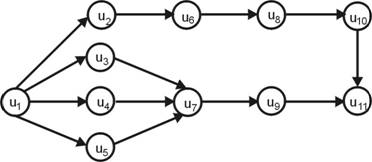
... не повторяются. Простой путь – путь, в котором дуги не повторяются. Маршрут – последовательность ребер, составляющих, как и путь, цепочку. Длина пути взвешенного графа определяется как сумма весов – его дуг. Если граф не взвешен, то можно считать веса дуг равными 1. Кратчайшим путем между выделенной парой вершин хн и хк называется путь, имеющий наименьшую длину среди всех возможных путей между ...
... единицы сравниваемых средств контроля, руб.; Т ,Т - сроки службы сравниваемых средств контроля, годы. 3 ПРОЕКТИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И СИСТЕМ РЕМОНТНОГО ПРОИЗВОДСТВА. Цель проектирования ТП – установление оптимальной последовательности и способов выполнения отдельных технологических операций ремонта изделия; подбор необходимого оборудования, оснастки и инструмента; определение ...
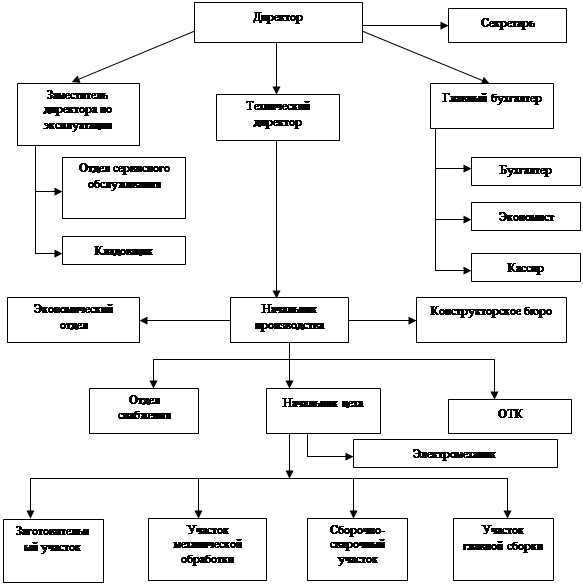
... распределения материальных благ и развития промышленного производства (сельского хозяйства, здравоохранения, связи и т. п.). Рис. 8.3. Структура системы управления общественным производством В реализации задачи инновационный менеджмент занимает специфическую и важную роль в установлении критериев и путей развития. 1 – Сбор данных и выделение ошибок. 2 – Анализ последствий ...
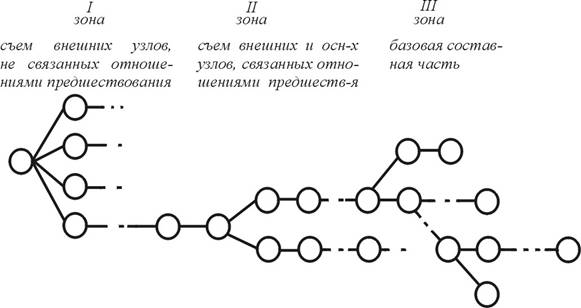
... телеги, микропроцессорные системы и т.д. В данном дипломном проекте поставлена задача оптимизировать сборку телеги, а также выявить экономический эффект за счет инноваций технологии и экономии ресурсов. Рассмотрим основные составляющие телеги: - Полка ТМ.201.01.03 – 24 шт. – Лист Б-О-ПН-2,0 ГОСТ 19903-74/12Х18Н10Т ГОСТ 5582-75; - Заглушка ТМ.201.01.09 – ...
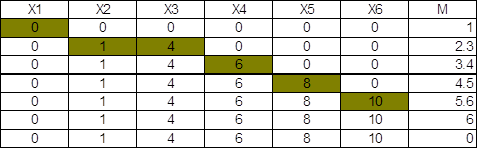

0 комментариев