Навигация
3.6 Пример работы алгоритма
Пусть задана таблица покрытий (см. Таб. 3). Рассмотрим пример работы алгоритма.
|
| B | B1 | B2 | B3 | B4 | B5 | B6 |
| А1 | 1 | 1 | 1 | |||
| А2 | 1 | 1 | 1 | |||
| A3 | 1 | 1 | 1 | |||
| А4 | 1 | 1 | 1 |
2. Множество антиядерных строк пустое .
3. Вычеркиваем столбцы В1, В3, В5, В6 как поглощающие
4. Вычеркиваем строку А2 как поглощенную.
Теперь таблица покрытий будет иметь вид
(см. Таб .4)
Таб. 4.
| В2 | В4 | |
| А1 | ||
| А3 | 1 | |
| А4 | 1 |
1. Множество ядерных строк Р={A3, A4}.
2. Множество антиядерных строк А={А1}.
3. Множество поглощающих столбцов пустое.
4. Множество поглощаемых строк пустое.
Теперь таблица покрытий примет вид (см. Таб 5)
| В2 | В4 | |
| А3 | 1 | |
| А4 | 1 |
Таким образом кратчайшее покрытие {A3, A4} Таб. 5.
4 АЛГОРИТМ НАХОЖДЕНИЯ КРАТЧАЙШЕГО ПУТИ В ГРАФЕ
4.1 Математическое описание задачи и методов её решения
Графом (G, X) называется совокупность двух конечных множеств: множества точек, которые называются вершинами (X = {Х1,...,Хn}), и множества связей в парах вершин, которые называются дугами, или ребрами ( (Хi, Хj) Î G ) в зависимости от наличия или отсутствия направленности связи.
Ребром называются две встречные дуги (Хi, Хj) и (Хj, Хi). На графе они изображаются одной линией без стрелки. Ребро, или дуга, конечные вершины которого совпадают, называется петлей.
Если на каждом ребре задается направление, то граф (G, Х) называется ориентированным. В противном случае граф называется неориентированным.
Две вершины, являющиеся конечными для некоторого ребра или некоторой дуги, называются смежными. Соответственно этот граф может быть представлен матрицей смежности либо матрицей инцидентности.
Матрицей инцидентности называется прямоугольная матрица с числом строк, равным числу вершин графа, и с числом столбцов, равным количеству ребер (дуг) графа. Элементы матрицы а задаются следующим образом: “1” ставится в случае если вершина vi, инцидентна ребру uj; “0” - в противном случае.
Вершина и ребро (дуга) называются инцидентными друг другу, если вершина является для этого ребра (дуги) концевой точкой.
Путь из начальной вершины хн к конечной вершине хк - последовательность дуг, начинающаяся в вершине хн Î Х, заканчивающаяся в вершине хк Î Х, и такая, что конец очередной дуги является началом следующей:
(хн, хi1)( хi1, хi2)( хi2… хik)( хik, xk) = (xн, хк).
Элементарный путь – путь, в котором вершины не повторяются.
Простой путь - путь, в котором дуги не повторяются.
Маршрут - последовательность ребер, составляющих, как и путь, цепочку.
Длина пути взвешенного графа определяется как сумма весов - его дуг. Если граф не взвешен, то можно считать веса дуг равными 1 .
Кратчайшим путем между выделенной парой вершин хн и хк называется путь, имеющий наименьшую длину среди всех возможных путей между этими вершинами.
Таким образом, нахождение кратчайшего пути – это поиск множества вершин, составляющих этот путь.
4.2 Словесное описание алгоритма и его работы
0. Инициализация кратчайших путей от вершины s до каждой вершины графа ∞, а все вершины 0, v=s.
1. Для каждой вершины u, смежной v, проверяем, отмечена ли она и какова длина пути между u и v. Если меньше, то запоминаем длину пути и текущую вершину u.
2. t= ∞, v=0. Для каждой вершины графа проверяем, отмечена ли она, и меньше ли путь от нее до s, чем t. Если так, то запоминаем её v=u, и её путь t=T[u] .
3. Если v=0, то пути нет, иначе если v=f, то путь найден и конец алгоритма.
4. Помечаем вершину v. Переход в п.1.
4.3 Выбор структур данных
Пусть p – количество вершин. Поскольку граф взвешен, то его представим в форме матрицы длин дуг:
С: array[1..p,1..p].
Используются следующие переменные и массивы:
s, f – вершины, между которыми следует найти кратчайший путь;
u, v – переменные циклов по вершинам;
T: array[1..p] of real – вектор, если вершина v лежит на кратчайшем пути от s к t, то T[v] – длина кратчайшего пути от s к v;
H: array[1..p] of 0..p – вектор, H[v] – вершина, непосредственно предшествующая v на кратчайшем пути;
X: array[1..p] of 0..1 – вектор меток вершин.
4.4 Описание схемы алгоритма
Блок-схема данного алгоритма изображена на рис. 4 в Приложении.
В блоке 1 происходит ввод графа в форме матрицы длин дуг, а также номеров вершин s и f. Далее организуется цикл по вершинам графа (блок 2). В нем инициализируются массив кратчайших путей и массив меток (блок 3): поскольку пути не известны, то они инициализируются бесконечностью, а метки – нулем. Далее отмечается вершина s, кратчайший путь от неё до неё же самой равен 0, и ей никто не предшествует; текущей вершиной v становится s (блок 5). Далее организовывается цикл по смежным с текущей вершинам (блок 6). В блоке 7 происходит проверка смежны ли вершины. В блоке 8 сравнивается уже имеющийся путь с путем между u и v. Если текущий меньше, то он и номер вершины запоминаются (блок 9).
В остальных блоках происходит поиск конца кратчайшего пути. Изначально его длина не известна (равна ∞), и вершина, оканчивающая его также не известна (блок 11). В блоке 12 организуется цикл по всем неотмеченным вершинам. В блоке 13 производиться сравнение уже имеющегося кратчайшего пути t с текущим T[u]. Если текущий меньше, то запоминаем его и вершину (блок 14). Далее производится анализ полученного конца пути. Если v=0 (блок 16), то не была найдена вершина конца кратчайшего пути, и, следовательно, нет такого пути (блок 17). Если же v=f (блок 18), то есть конец совпадает с заданной вершиной, то между ними существует кратчайший путь (блок 19). В обоих случаях конец алгоритма.
Если же не достигнута заданная вершина f, то текущая вершина v помечается (блок 20) и переход в блок 6.
Алгоритм работает, пока не будет вершина t либо пока не станет ясно, что пути из s в f нет.
4.5 Контрольный пример решения задачи с помощью алгоритма поиска кратчайшего пути
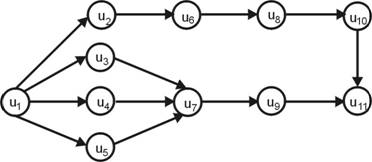
Пусть задан граф, изображенный на рис. 1. Рассмотрим на этом примере работу алгоритма.
0. for v=1..p
T[v]=∞;
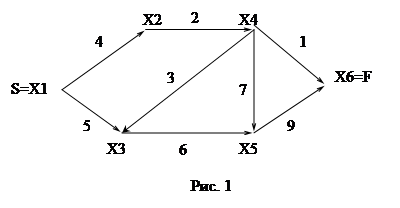 X[v]=0;
X[v]=0;
H[s]=0;
T[s]=0;
X[s]=1;
v=s;
1. X2 ? G(1) →
X[2]=0&(∞>0+4) →
T[2]=T[1]+C[1,2]=4;
H[2]=1;
X3 ? G(1) →
X[3]=0&(∞>0+5) →
T[3]=T[1]+C[1,3]=5;
H[3]=1;
2. t=∞; v=0;
for u=1..p
X[2]=0&T[2]=4<∞ →
v=2; t=T[2]=4;
X[3]=0&T[3]=5!< ∞
3. v=2≠0;
v=2≠f=6;
4. X[2]=1 → п.1;
1. X4 ? G(2) →
X[4]=0&(∞>0+2) →
T[4]=T[2]+C[2,4]=6;
H[4]=2;
2. t=∞; v=0;
for u=1..p
X[4]=0&T[4]=6<∞ →
v=4; t=T[4]=6;
3. v=4≠0;
v=4≠f=6;
4. X[4]=1 → п.1;
1. X3 ? G(4) →
X[3]=0&(5!>6+3)
X5 ? G(4) →
X[5]=0&(∞>0+7) →
T[5]=T[4]+C[4,5]=13;
H[5]=4;
X6 ? G(4) →
X[6]=0&(∞>0+1) →
T[6]=T[4]+C[4,6]=7;
H[6]=4;
2. t=∞; v=0;
for u=1..p
X[3]=0&T[3]=5<∞ →
v=3; t=T[3]=5;
X[5]=0&T[5]=13!< 5
X[6]=0&T[6]=1<5 →
v=5; t=T[5]=7;
3. v=6≠0;
v=6=f=6; → конец алгоритма.
ЗАКЛЮЧЕНИЕ
В данной работе разработаны алгоритмы сортировки, поиска кратчайшего пути в графе и поиска покрытия, близкого к кратчайшему. Алгоритмы исполнены с нужной степенью детализации, необходимой для понимания их работы. Рассмотрены пути улучшения эффективности каждого алгоритма учитывая требования конкретной задачи.
Большое внимание уделено сравнению возможного использования нескольких структур данных, проведён анализ эффективности работы алгоритма в зависимости от используемой структуры.
Рассмотрена сложность каждого алгоритма, её зависимость от условий данной задачи, методы упрощения и облегчения понимания алгоритма.
ЛИТЕРАТУРА
1. Вирт Н. Алгоритмы и структуры данных. – С.-П.: Невский диалект, 2001. – 350 с.
2. Новиков Ф.А. Дискретная математика для программистов. – С.-П.: Питер, 2003.–292 с.
3. Шендрик Е.В. Конспект лекций по дисциплине «Теория алгоритмов». – Одесса, 2003.
Похожие работы
... не повторяются. Простой путь – путь, в котором дуги не повторяются. Маршрут – последовательность ребер, составляющих, как и путь, цепочку. Длина пути взвешенного графа определяется как сумма весов – его дуг. Если граф не взвешен, то можно считать веса дуг равными 1. Кратчайшим путем между выделенной парой вершин хн и хк называется путь, имеющий наименьшую длину среди всех возможных путей между ...
... единицы сравниваемых средств контроля, руб.; Т ,Т - сроки службы сравниваемых средств контроля, годы. 3 ПРОЕКТИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И СИСТЕМ РЕМОНТНОГО ПРОИЗВОДСТВА. Цель проектирования ТП – установление оптимальной последовательности и способов выполнения отдельных технологических операций ремонта изделия; подбор необходимого оборудования, оснастки и инструмента; определение ...
... распределения материальных благ и развития промышленного производства (сельского хозяйства, здравоохранения, связи и т. п.). Рис. 8.3. Структура системы управления общественным производством В реализации задачи инновационный менеджмент занимает специфическую и важную роль в установлении критериев и путей развития. 1 – Сбор данных и выделение ошибок. 2 – Анализ последствий ...
... телеги, микропроцессорные системы и т.д. В данном дипломном проекте поставлена задача оптимизировать сборку телеги, а также выявить экономический эффект за счет инноваций технологии и экономии ресурсов. Рассмотрим основные составляющие телеги: - Полка ТМ.201.01.03 – 24 шт. – Лист Б-О-ПН-2,0 ГОСТ 19903-74/12Х18Н10Т ГОСТ 5582-75; - Заглушка ТМ.201.01.09 – ...
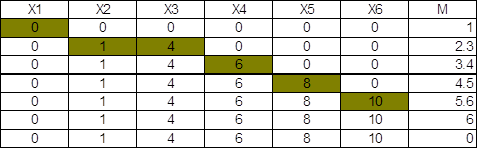

0 комментариев