Навигация
Метод початкових параметрів
5. Метод початкових параметрів
Аналіз попередніх рішень показує, що при деякім перетворенні диференціальні рівняння можна скласти так, що вони будуть придатні при будь-якому виді завантаження. Зосереджені сили P1, Р2? …, розташовані на відстанях l1, l2, l3, … від початку координат, у рівняннях прогинів запишуться так:
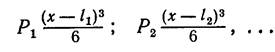 (48)
(48)
Зосереджені моменти М1, М2,... з тими ж відстанями від початку координат дадуть у рівнянні
![]() (49)
(49)
Рівномірно розподілені навантаження q1, q2,..., що починаються у відстанях l1, l2, … від початку координат і розташовані далі неперервно, дають вираження
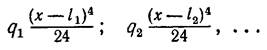 (50)
(50)
Помітимо, що коефіцієнт у знаменниках (84)... (50) не що інше, як
24 = 1 • 2 • 3. 4 = 4!
6 = 1 • 2 • 3 = 3!
2 = 1 • 2 = 2!
1 = 1 = 1! (51)
Довільні постійні при прийнятому вище порядку складання виражень М(х) і порядку інтегрування будуть на всіх ділянках однакові і можуть бути замінені через збільшені в EJ раз прогин у0 і кут повороту q0 на початку координат (звідси і метод початкових параметрів).
Розташовуючи члени рівнянь по висхідним ступенях х, заміняючи l1, l2, … через l0 і підсумовуючи всі однотипні члени, можемо скласти наступні загальні рівняння пружної лінії:
рівняння кутів повороту
![]() (52)
(52)
рівняння прогинів
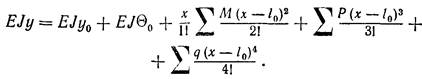 (53)
(53)
Якщо в перетині балки, що збігає з початком координат, діє сила P0 і момент М0, то їх прийнято називати статичними, початковими параметрами Для випадку декількох моментів і сил, а також декількох ділянок розподіленого навантаження універсальне рівняння пружної лінії записують у наступній формі:
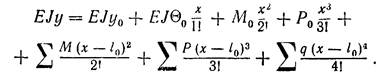 (54)
(54)
Рівняння кутів повороту завжди може бути отримано безпосереднім диференціюванням рівняння пружної лінії на відповідній ділянці балки. Таким чином, визначення переміщень по методу початкових параметрів зводиться в першу чергу до визначення значень початкових параметрів у0, q0, Р0, М0.
Необхідно пам'ятати, що закон Гука справедливий не тільки для матеріалу, але і для всієї балки в цілому: прогини і кути повороту прямо пропорційні навантаженням. Ця обставина дозволяє у випадку складного навантаження одержувати рівняння вигнутої осі як суму ординат кривих, що відповідають приватним навантаженням. Особливо це спрощується при обчисленні найбільшого прогину.
6. Диференціальні залежності при вигині
У розділі про вигин балки встановлені наступні диференціальні залежності:
для суцільного навантаження
![]() (55)
(55)
для поперечної сили
 (56)
(56)
для згинаючого моменту
![]() (57)
(57)
для кута повороту перетину
![]() (58)
(58)
Ці залежності можна розташувати послідовно:
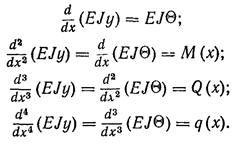 (59)
(59)
Отже, знаючи навантаження q (х) і пристрій опор балки, можна послідовним інтегруванням одержати Q (х}, М (х), EJq, EJy, а знаючи рівняння вигнутої осі, можна шляхом послідовного диференціювання по х з функції EJy одержати EJq, М (х), Q (х) і q (х).
Для графічного зображення цих залежностей умовимося позитивні значення перерахованих значень відкладати нагору, вісь х — вправо, поворот перетину — проти вартовий стрілки.
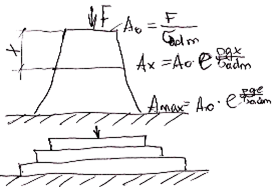
7. Балки перемінного перетину. Бруси рівного опору вигину
Дотепер розглядалися балки з постійними розмірами поперечних переріз по всій довжині. В більшості випадків на балку діють навантаження так, що згинальні моменти в перетинах балки перемінні і змінюються за законом чи прямої кривої.
Розміри поперечного переріза балки підбираються по формулі
 (60)
(60)
Отже, у балках постійного перетину матеріал витрачається неекономно. Щоб уникнути цього необхідно розміри поперечних переріз балки підбирати відповідно до М (х) і допустимим напруженням [s], тобто щоб у всіх поперечних перерізах smax, виникаючі під впливом зовнішніх сил, що діють на балку, не перевершували що допускаються
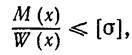 (61)
(61)
звідкіля
 (62)
(62)
тобто W (х) для кожного перетину повинний мінятися пропорційно М (х).
Умови (61) і (62) справедливі і для перетину з найбільшим згинальним моментом Мmax, де W (х) = W0;
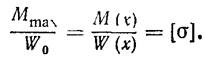 (63)
(63)
Ці вимоги можуть бути задоволені, якщо перетин балок робити перемінним. Такі балки легше по вазі, вони більш гнучкі. Ці властивості особливо необхідні пластинчастим пружинам, ресорам і ін. Балки рівного опору вигину розраховуються з умов міцності і твердості Найбільше поширення одержали балки рівного опору у виді прямокутника — з перемінною шириною b (х) і постійною висотою h чи з постійною шириною і перемінною висотою (ресори, плоскі пружини й ін.). Часто зустрічаються балки рівного опору вигину (вали, осі я ін.) круглого перетину.

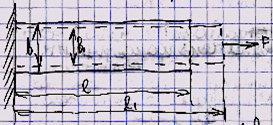
Мал. 9
Розглянемо балку прямокутного перетину з b = b (х) і h = const (мал. 9)
Диференціальне рівняння вигнутої осі має вид
![]() (64)
(64)
де
![]() (65)
(65)
Значення b(х) визначимо з умов (63) з обліком того, що момент опору в перетині на відстані х від вільного кінця буде ![]() , а М (х) = -Pх; момент опору опорного перетину
, а М (х) = -Pх; момент опору опорного перетину ![]() , а найбільший згинальний момент в опорному перетині Мmax = -Рl, тоді
, а найбільший згинальний момент в опорному перетині Мmax = -Рl, тоді
![]() (66)
(66)
З (65) з обліком (66) знайдемо
![]() (67)
(67)
де j0 - момент інерції опорного перетину.
Таким чином, рівняння (64) буде мати вид
![]() (68)
(68)
Інтегруючи, одержимо
![]()
Постійні визначаємо з граничних умов: при х = l у' = 0 відкіля ![]() ; при х = l у = 0, відкіля
; при х = l у = 0, відкіля ![]()
Тоді
![]() (69)
(69)
Максимальні деформації рівні будуть при х = 0 на вільному кінці балки.
![]() (70)
(70)
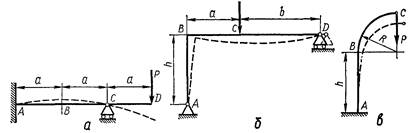
Мал. 10
Порівнюючи ці значення q і f значеннями для балки постійного перетину, бачимо, що деформації (70) q у два, а у в 1,5 рази більше, ніж у брусів постійного перетину.
Таким чином, балки перемінного перетину мають більшу гнучкість у порівнянні з балками постійної твердості при однаковій з ними міцності. Саме тому, а не заради економії матеріалу їх і застосовують у таких конструкціях, як ресори, пружини й ін.
8. Потенційна енергія деформації при вигині
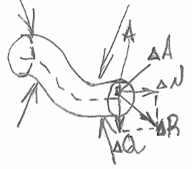
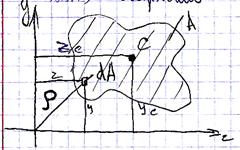
Крім розглянутих способів обчислення у і q перетинів балок існує більш загальний метод, заснований на застосуванні закону збереження енергії і придатний для визначення деформацій будь-яких пружних конструкцій (систем). Під пружною системою будемо розуміти систему стрижнів, чи шарнірно жорстко зв'язаних між собою (мал. 10).
При статичній дії навантажень відбувається перетворення потенційної енергії з одного виду в іншій. Повне перетворення енергії з одного виду в іншій має місце тільки тоді, коли деформація відбувається без порушення рівноваги системи. Закон збереження енергії при деформації пружних систем приймає вид
![]() (71)
(71)
Рівність (71) показує, що при переміщеннях без порушення рівноваги сума робіт усіх сил, прикладених до крапок тіла, дорівнює нулю і що потенційна енергія деформації U численно дорівнює роботі зовнішніх сил Ар, проробленої ними при цій деформації,
![]() (72)
(72)
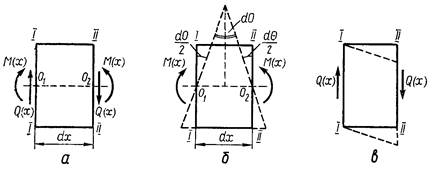
Мал. 8.11
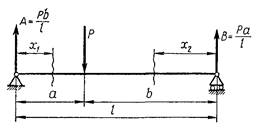
Мал. 12
При обчисленні потенційної енергії будемо припускати, що деформації пропорційні навантаженням і ростуть постійно разом з ними. Аналогічно, як і при розтяганні, зрушенні, крутінні, обчислимо потенційну енергію при чистому вигині
 (73)
(73)
тобто потенційна енергія деформації дорівнює половині добутку сили (розтягання, зрушення) чи пари сил (крутіння, вигин) па переміщення крапки додатка цієї сили по напрямку сили. Умовимося називати терміном «узагальнена сила» усяке навантаження, яке викликає відповідне навантаженню переміщення, тобто зосереджену силу чи пару сил; переміщення, що відповідає цій силі, будемо називати «узагальненою координатою». Тоді формула для потенційної анергії при різних видах деформації узагальнюється
![]() (74)
(74)
де Р — узагальнена сила; d — узагальнена координата.
У загальному випадку вигину згинальний момент М (х) — значення перемінне. У будь-якому перетині йому буде супроводжувати поперечна сила Q (х) Тому розглядати випливає не всю балку в цілому, а лише нескінченно малий елемент балки довжиною dx При дії згинаючих зусиль перетину елемента повертаються й утворять між собою кут d (мал. 11). Дотичні зусилля прагнуть викликати перекіс елемента. Звичайно робота дотичних зусиль виявляється малої в порівнянні з роботою нормальних зусиль, тому нею зневажаємо. Елементарна ж робота нормальних зусиль дорівнює
![]() (75)
(75)
Уся потенційна енергія виходить підсумовуванням по довжині балки
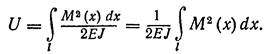 (76)
(76)
У тих випадках, коли маємо дві і більш ділянки для М (х), інтеграл (8.76) розбиваємо на суму інтегралів
 (77)
(77)
Як приклад розглянемо балку на двох опорах (мал. 12) із зосередженою силою. Обчислимо за допомогою потенційної енергії прогин під силою Р. Епюра моменту має дві ділянки, тому і потенційну енергію (77) обчислимо по формулі
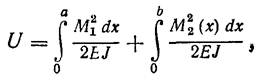
де

і тоді
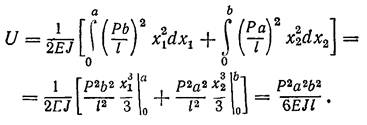 (78)
(78)
Відповідно до формул (72) і (75) з обліком того, що з зовнішніх сил тільки сила Р робить роботу при деформації балки,
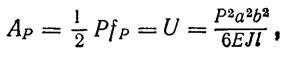
одержимо прогин під цією силою
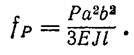 (79)
(79)
Якщо сила прикладена посередині  , то одержимо уже
, то одержимо уже
відоме вираження прогину
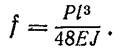
Похожие работы
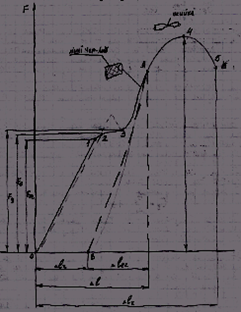
... дбувається за рахунок так званого „внутрішнього тертя”. Т 4 відповідає границі міцності матеріалу σu = Fu/Ao σu – границя міцності матеріалу – найб норм напруга до руйнування. 8. Метод розрахунків в ОМ. Основні види задач ОМ Статично невизначена задача визначення силового стану конструкції розв’язують розглядаючи 4 сторони задачі: 1 – статична сторона задачі: складають всі ...
... лише в деяких випадках, то практичне значення має зміна С за рахунок зміни закріплення країв пластини. Зміну товщини чи схеми кріплення плати можна здійснити практично завжди. 2.9 Віброзахист обчислювальної техніки Всі види радіоелектронної апаратури зазнають зовнішніх або внутрішніх механічних дій. Механічні дії передаються кожному елементу і викликають їх вібрації. Викликані вібрації ...
... Через отримані точки проводимо плавну криву. Відкладаємо значення діаметрів находимо точки В і Н, проводимо вхідну кромку канатки робочого колеса. 2.9. КІНЕМАТИЧНИЙ ТА СИЛОВИЙ РОЗРАХУНОК ПРИВОДУ Визначаємо параметри на валу ротора насосу =0,98 – ККД витрат в муфті = 0,99 – ККД витрат в підшипниках 2.10. РОЗРАХУНОК І ВИБІР МУФТ ТА ГАЛЬМА Визначаємо номінальний момент, який ...
... технічних забезпеченість експедицій та залежність від існуючої тоді командно-адміністративної системи. Але незважаючи на це, в ці роки відбулися яскраві події, які заклали міцний фундамент для подальшого розвитку гідроархеології Дніпра – підйом носової частини парусно-гребного човна в 1971 році [8],[3]. Авторитет запорізьких гідроархеологів був таким великим, що саме в Запоріжжі в 1987 році було ...

0 комментариев