Метод Брауна

1.3.3. Метод Брауна

Метод Брауна основан на использовании адаптивных моделей разного порядка. Адаптивные модели первого порядка основаны на использовании экспоненциальной средней, отличие состоит в выборе . Начальные условия для расчета:

(1.19)

где

, где

 — это шаг.

Расчет производится по следующим формулам:

	(1.20)
	(1.21)

Прогноз следующего значения ряда вычисляется по следующей формуле:

(1.22)

Для построения графических зависимостей пользуются столбцами значений: х и .

1.3.4. Метод среднего темпа

При использовании этого метода в расчете учитывается вся информация ряда. Расчет базируется на предпосылке о том, что сумма фактических уровней динамического ряда или суммарный рост за период должен быть равен сумме уровней, полученных расчетным путем исходя из начального уровня ряда и среднего темпа роста ().

Он производится по формуле:

(1.23)

Расчет уровня ряда:

,

(1.24)

где .

Расчет проводится путем подбора  при соблюдении следующего условия:

(1.25)

Когда определено значение , при котором , найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок.

Высчитывается по формуле:

(1.26)

2. Статистический показатель расчетов

временных рядов (корреляция)

 

Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайная величина называется дискретной, если ее возможные значения можно пронумеровать. Основными формами задания дискретной случайной величины являются: 1) ряд распределения; 2) функция распределения (интегральная функция распределения).

Математическое ожидание дискретной случайной величины Х называется значение, рассчитанное по формуле

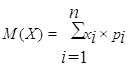. (2.1)

Математическое ожидание обозначается также m_x. Оно приближенно равно среднему возможному значению случайной величины.

Случайная величина называется непрерывной, если ее возможные значения сплошь заполняют некоторый интервал. Основными формами задания непрерывной случайной величины являются:

·           интегральная функция распределения F(x);

·           функция плотности вероятности f(x).

Интегральная функция распределения для непрерывной случайной величины Х определяется так же, как и для дискретной F(x) = P(X < x).

Плотность вероятности (дифференциальной функцией распределения) случайной величины Х называется функция

f(x) = F^´(x). (2.2)

Для непрерывной случайной величины Х функция распределения F(x) непрерывна на всей оси Ох, а плотность вероятности f(x) существует везде, за исключением, может быть, конечного числа точек.

Математическим ожиданием m_x непрерывной случайной величины Х, для которого функция f(x) является плотностью вероятности, называется величина несобственного интеграла

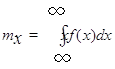, (2.3)

если он сходится.

Дисперсией называется значение несобственного интеграла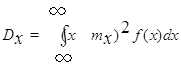

, (2.4)

если он сходится.

При вычислении дисперсии иногда удобна формула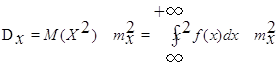

. (2.5)

Кроме математического ожидания для характеристики положения центра распределения случайной величины часто используют моду и медиану. Модой называется то значение случайной величины, которому соответствует наибольшая плотность вероятности ее распределения.

Медианой называется значение случайной величины, для которой интегральная функция распределения F(x) = 0,5.

Для того чтобы рассчитать значения моды и медианы, необходимо вначале определить модальный и медиальный интервал. Модальный интервал на гистограмме отвечает наибольшей частоте попадания случайной величины. Моду рассчитывают по формуле

, (2.6)

где Х_Мо– нижняя граница модального интеграла; С – величина интервала (разность между верхней и нижней границами); Δ₁ – разность числа попаданий случайной величины в модальный интервал и предыдущий интервал; Δ₂ – разность попаданий случайной величины в модальный интервал и последующий интервал.

Медиальный интервал определяется по формуле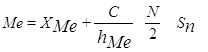

, (2.7)

где Х_Ме – нижняя граница медиального интервала С; h_Ме – количество попаданий случайной величины в медиальный интервал; N – общее количество опытов; S_n – сумма исходов, соответствующих попаданию случайной величины в интервалы, не превышающие количество N/2.

 

Корреляция

Существуют две категории связей или зависимостей между признаками: функциональные и корреляционные. При функциональной зависимости каждому значению одной переменной соответствует одно значение другой переменной.

Связь случайной величины всегда носит вероятностный характер. Следовательно одному значению одной случайной величины соответствует несколько значений другой случайной величины. Такая зависимость называется корреляционной.

Самым простым случаем вероятностной связи является корреляция двух факторов — парная корреляция. Наглядное представление о парной корреляции дает корреляционное поле — графическое изображение точек, координаты которых соответствуют значениям случайных величин.

Различают положительную и отрицательную корреляции. При положительной корреляции зависимость между случайными величинами прямая, т. е. при увеличении значений одной случайной величины увеличиваются и значения второй случайной величины. При отрицательной корреляции увеличению значений одной случайной величины соответствует уменьшение значений второй случайной величины.

Связь двух факторов тем больше, чем теснее располагаются точки около некоторой линии, отображающей график зависимости одной случайной величины от другой. Если все точки корреляционного поля попадают на эту линию, то теснота связи окажется максимальной, и получается функциональная зависимость двух случайных величин. Для количественного определения тесноты связи между двумя случайными величинами в случае линейной корреляции используют коэффициент корреляции, который может быть определен по двум следующим формулам:

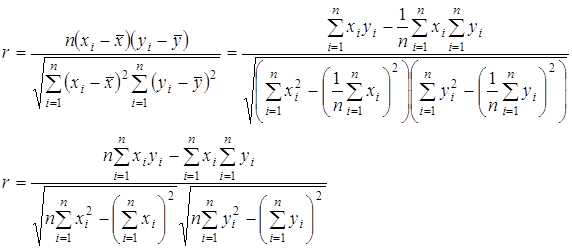, (2.8)

где x_i, y_i — текущие значения случайных величин;

 — средние значения случайных величин.

Если r = 0, то случайные величины не связаны между собой. В этом случае точки, составляющие корреляционное поле располагаются по кругу от усредняющей линии регрессии, которая параллельна оси Ох. Если r = 1, то имеем положительную функциональную зависимость, все точки которой принадлежат одной прямой; если r = -1 — отрицательную. Чаще всего r равно промежуточному значению. В этом случае между переменными существует корреляционная зависимость, а все точки располагаются в виде эллипса вокруг линии регрессии. Чем теснее связь между случайными величинами, тем ближе |r| к единице.

ЗАКЛЮЧЕНИЕ

Задачей данного курсового проекта является проведение статистического анализа и прогнозирование результатов выпуска изданий (Беларуси и России).

В процессе выполнения курсового проекта мы ознакомились с основными понятиями теории вероятностей, которыми являются случайный эксперимент, события и вероятности, и математической статистики, занимающиеся восстановлением закономерностей и подчиняющие массовые однородные случайные явления на основе изучения статистических данных — результатов наблюдений; а также изучили современные методы линейного программирования и теории статистических игр.

В курсовой работе был проведен статистический анализ и прогнозирование деятельности издательств России и Беларуси с помощью следующих четырех методов:

-           метод экспоненциального сглаживания;

-           метод скользящего среднего;

-           метод среднего темпа;

-           метод Брауна.

В результате расчетов был получен прогноз деятельности издательств на 2003 год.

Из таблиц в приложениях можно сделать вывод, что метод экспоненциального сглаживания дает более точный прогноз.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1.         Губарев А. А. Моделирование и оптимизация технологических процессов редакционно-издательских технологий. – Мн., 2005.

2.         Пен Р. З. Статистические методы моделирования и оптимизации процессов целлюлозно-бумажного производства.— Красноярск, 1982.

3.         Саркисяна С.А. Теория прогнозирования и принятия решений [Текст]/ Под ред. С. А. Саркисяна.— М., 1977.

4.         Четыркин Е. М. Статистический метод прогнозирования.— М., 1977.