Навигация
Формы собственных колебаний здания
3.2 Формы собственных колебаний здания
Величина ![]() - смещение точек динамической системы отвечает уравнению собственных (свободных) колебаний. В практических расчетах уравнение
- смещение точек динамической системы отвечает уравнению собственных (свободных) колебаний. В практических расчетах уравнение ![]() аппроксимируют в виде тригонометрических полиномов. Для определения коэффициента формы колебаний в формулу (2.3) подставляют не абсолютные смещения точек, а лишь их отношения. Например, формы трех тонов свободных колебаний многоэтажных зданий:
аппроксимируют в виде тригонометрических полиномов. Для определения коэффициента формы колебаний в формулу (2.3) подставляют не абсолютные смещения точек, а лишь их отношения. Например, формы трех тонов свободных колебаний многоэтажных зданий: ![]() , (2.4)
, (2.4)
где ![]() - безразмерная координата точки j.
- безразмерная координата точки j.
Относительные координаты форм свободных колебаний даны в табл. 2.1 для трех ортонормированных функций.
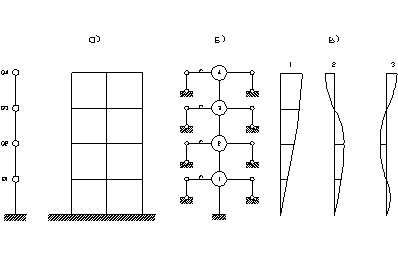
Рис. 3.3- К динамическому расчету 4-этажного здания:
а – условная схема здания; б – расчетная схема при определении периодов и форм свободных колебаний горизонтальных колебаний; в – три ортонормированные функции, аппроксимирующие формы свободных колебаний.
3.3 Оценка влияния продольных сил в сечении колонн на динамические характеристики каркаса
Изгибная жесткость рамы:
Во =EbAL2/2=16500∙0,4 ∙0,4∙152/2 =2970∙105 кН∙м2, (3.8)
где L= 15 м- расстояние между осями крайних колонн.
Характеристика жесткости рамы при учете влияния продольных сил в сечении колонн, по формуле ![]() . (3.9)
. (3.9)
Следовательно, учитывать влияние продольных сил в сечении колонн на динамические характеристики рамного каркаса не требуется.
3.4 Усилия в сечениях элементов рамы от сейсмической нагрузки
Так как расчетные сейсмические нагрузки по п. 2.3 [10] принимаются, действующими в горизонтальном направлении, вертикальная составляющая сейсмических сил не учитывается. Так же не учитывают по п. 2.4 [10] вертикальную сейсмическую нагрузку для рам пролетом менее 24 м. Расчетные значения поперечных сил и изгибающих моментов в сечениях элементов рамы по п. 2.10 [10] следует определить по формулам:
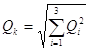 и
и 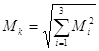 ;
;
в которых Qi и Mi — усилия в рассматриваемом сечении, вызываемые сейсмическими нагрузками, соответствующими форме колебаний i.
В приближенном расчете многоэтажных рам на горизонтальные нагрузки учитывают уменьшение жесткости крайних колонн, так как они имеют меньшую степень защемления в узлах, чем средние колонны.
Погонные жесткости элементов рамы 1-го этажа:
ригеля ![]()
где![]()
колонны 2-го этажа ![]()
где ![]()
колонны 1-го этажа ![]()
Табличный коэффициент ![]()
При отношении погонных жесткостей ригелей и колонн ![]()
согласно табл. XV.1 [1], общая жесткость колонн рамы (принимая за единицу жесткость средней колонны):
на 1-ом этаже ∑i = 1+2∙0,9 = 2,8; на других этажах ∑i = 1+2∙(0,54+0,54)-2 = 1,16;
Поперечные силы в сечениях средних колонн рамы:
на 1-м этаже ![]() 2,8=(242,44+39,30+68,58)/2,8=125,11;
2,8=(242,44+39,30+68,58)/2,8=125,11;
со 2-го по 5-й этаж ![]() 1,16= (86,59+14,04+24,49)/1,16=107,86;
1,16= (86,59+14,04+24,49)/1,16=107,86;
Изгибающие моменты в сечениях средних колонн:
на 1-м этаже в сечении под ригелем рамы М1=2∙Q1l/3;
в сечении по с 2-го по 4-й этаж Мk=Q1l/2; где l- расчетная длина колонн, равная высоте этажа.
Поперечные силы (кН) и изгибающие моменты (кН∙м) в сечениях средних колонн рамы подсчитаны в таблице 4.1 для трёх форм колебаний.
4 Определение сейсмических нагрузок и усилий от них
Коэффициенты форм колебаний ηik для трех тонов подсчитаны в табл. 3.2 с использованием относительных координат форм свободных колебаний, приведенных в табл. 4.1. по формуле:
![]() ; (4.1)
; (4.1)
где![]() - смещение точек здания при собственных колебаниях по
- смещение точек здания при собственных колебаниях по ![]() -му тону в рассматриваемой точке k и во всех точках j расположения ярусных нагрузок
-му тону в рассматриваемой точке k и во всех точках j расположения ярусных нагрузок ![]() .Расчетную сейсмическую нагрузку
.Расчетную сейсмическую нагрузку ![]() в выбранном направлении действия, приложенную к точке k и соответствующую
в выбранном направлении действия, приложенную к точке k и соответствующую ![]() -му тону свободных, т.е. собственных колебаний здания, определяют по формуле п. 2.5[10]:
-му тону свободных, т.е. собственных колебаний здания, определяют по формуле п. 2.5[10]: ![]() , (4.2)
, (4.2)
Таблица 4.1
| Этажи |
|
кН |
|
|
|
кН |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0,241 | 1125,09 | 0,3698 | 0,1368 | 416,10 | 153,89 | 0,463 |
| 2 | 0,483 | 1125,09 | 0,6872 | 0,4723 | 773,20 | 531,36 | 0,860 |
| 3 | 0,724 | 1125,09 | 0,9072 | 0,8230 | 1020,65 | 925,90 | 1,135 |
| 4 | 1,000 | 772,45 | 1,0000 | 1,0000 | 772,45 | 772,45 | 1,251 |
| Итого | 2982,39 | 2383,60 | |||||
| 1 | 0,241 | 1125,09 | 0,9072 | 0,8230 | 1020,65 | 925,90 | 0,302 |
| 2 | 0,483 | 1125,09 | 0,7634 | 0,5828 | 858,91 | 655,70 | 0,254 |
| 3 | 0,724 | 1125,09 | -0,2647 | 0,0701 | -297,84 | 78,85 | -0,088 |
| 4 | 1,000 | 772,45 | -1,0000 | 1,0000 | -772,45 | 772,45 | -0,333 |
| Итого | 809,27 | 2432,89 | |||||
| 1 | 0,241 | 1125,09 | 0,2361 | 0,0557 | 265,65 | 62,72 | 0,111 |
| 2 | 0,483 | 1125,09 | -0,7761 | 0,6023 | -873,16 | 677,64 | -0,364 |
| 3 | 0,724 | 1125,09 | 0,7434 | 0,5526 | 836,35 | 621,71 | 0,349 |
| 4 | 1,000 | 772,45 | 1,0000 | 1,0000 | 772,44 | 772,44 | 0,469 |
| Итого | 1001,28 | 2134,52 |
где ![]() - коэффициент, учитывающий допускаемые повреждения зданий и принимаемый по табл. 3 [10],
- коэффициент, учитывающий допускаемые повреждения зданий и принимаемый по табл. 3 [10], ![]() - для зданий и сооружений, в конструкциях которых могут быть допущены остаточные деформации и повреждения, затрудняющие нормальную эксплуатацию, при обеспечении безопасности людей и сохранности оборудования, возводимые с железобетонным каркасом с диафрагмами или связями;
- для зданий и сооружений, в конструкциях которых могут быть допущены остаточные деформации и повреждения, затрудняющие нормальную эксплуатацию, при обеспечении безопасности людей и сохранности оборудования, возводимые с железобетонным каркасом с диафрагмами или связями; ![]() - коэффициент, учитывающий характеристики конструкций и принимаемый по табл. 6 [10],
- коэффициент, учитывающий характеристики конструкций и принимаемый по табл. 6 [10], ![]() для каркасных зданий, стеновое заполнение которых не оказывает влияния на их деформативность;
для каркасных зданий, стеновое заполнение которых не оказывает влияния на их деформативность; ![]() - коэффициент, учитывающий расчетную сейсмичность площадки строительства и определяемый по п. 2.5 [10],
- коэффициент, учитывающий расчетную сейсмичность площадки строительства и определяемый по п. 2.5 [10], ![]() при сейсмичности 9 баллов;
при сейсмичности 9 баллов; ![]() - коэффициент динамичности, определяемый по п. 2.6* [10];
- коэффициент динамичности, определяемый по п. 2.6* [10]; ![]() - коэффициент, зависящий от формы деформации здания при свободных колебаниях по
- коэффициент, зависящий от формы деформации здания при свободных колебаниях по ![]() -му тону и от места расположения нагрузки k и определяемый по п.2.7 [10]:
-му тону и от места расположения нагрузки k и определяемый по п.2.7 [10]: ![]() , (2.3)
, (2.3)
где![]() - смещение точек здания при собственных колебаниях по
- смещение точек здания при собственных колебаниях по ![]() -му тону в рассматриваемой точке k и во всех точках j расположения ярусных нагрузок
-му тону в рассматриваемой точке k и во всех точках j расположения ярусных нагрузок ![]() .
.
![]()
![]()
Таблица 4.2
| Э т а ж и |
|
кН | Первая форма колебаний с
| Вторая форма колебаний с
| Третья форма колебаний с |
| ||||||||||||||||
|
|
|
|
|
|
|
| ||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| |||||||||||||
| 4 | 1,000 | 772,45 | 1,251 | 62,793 | -0,333 | -37,51371 | 0,469 | 52,90263 |
| |||||||||||||
| 3 | 0,724 | 1125,09 | 1,135 | 82,97 | -0,088 | -14,46462 | 0,349 | 57,27951 |
| |||||||||||||
| 2 | 0,483 | 1125,09 | 0,860 | 62,854 | 0,254 | 41,712734 | -0,364 | -59,8004 |
| |||||||||||||
| 1 | 0,241 | 1125,09 | 0,463 | 33,825 | 0,302 | 49,567386 | 0,111 | 18,19347 |
| |||||||||||||
| Этаж k | Первая форма колебаний | Вторая ф࠾рма к࠾࠻еба࠽ий | Третья форма колебаний | ||||||||||||||||||||
| S1k | ∑S1k | Qk | Мk | S2k | ∑S2k | Qk | Мk | S3k | ∑S3k | Qk | Мk | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||||||||||
| 4 | 62,79 | 62,79 | 54,13 | 94,73 | -37,51 | -37,51 | -32,34 | -56,59 | 52,90 | 52,90 | 45,61 | 79,81 | |||||||||||
| 3 | 82,97 | 145,76 | 125,66 | 219,90 | -14,46 | -51,98 | -44,81 | -78,42 | 57,28 | 110,18 | 94,98 | 166,22 | |||||||||||
| 2 | 62,85 | 208,62 | 179,84 | 314,72 | 41,71 | -10,27 | -8,85 | -15,49 | -59,80 | 50,38 | 43,43 | 76,01 | |||||||||||
| 1 | 33,83 | 242,44 | 86,59 | 101,02 | 49,57 | 39,30 | 14,04 | 16,38 | 18,19 | 68,58 | 24,49 | 28,57 | |||||||||||
| M= | 202,04 | M= | 32,75 | M= | 160,01 | ||||||||||||||||||
Находим значение сейсмических сил по формуле:
![]() (4.3)
(4.3)
![]()
![]()
![]()
![]()
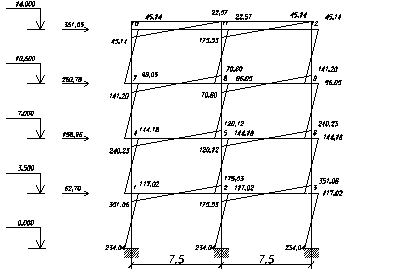
4.1 – К расчету поперечной рамы на горизонтальную нагрузку
Ярусные поперечные силы:
4-й этаж ![]()
3-й этаж ![]()
2-й этаж ![]()
1-й этаж ![]()
Изгибающие моменты в стойках:
4-й этаж ![]()
3-й этаж ![]()
2-й этаж ![]()
1-й этаж ![]()
![]()
Изгибающие моменты в ригелях:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
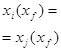
0 комментариев