Навигация
Определение размеров сечения ригеля
1. Определение размеров сечения ригеля.
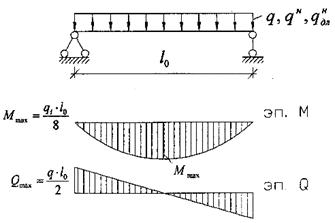
Для уточнения предварительно принятых размеров сечения ригеля вычисляется требуемая высота на основании упрощенного расчета. Опорный момент приближенно принимаем равным: М=(0,6…0,7)*М0, где М0=Рпер*L2/8–изгибающий момент в ригеле, вычисленный как для однопролетной балки.
М0=126.428*6.42/8=647.309 кН*м.
М=0,7*647.309=453.117 кН*м.
Примем бетон ригеля марки B25, с расчетным сопротивлением сжатию: Rb=14.5 МПа, тогда рабочая высота ригеля:
h0=![]() =(453.117/(0.2888*14.5*0.3*1000))0,5=0.6006 м=60.06 см,
=(453.117/(0.2888*14.5*0.3*1000))0,5=0.6006 м=60.06 см,
где А0опт=ξопт*(1-0,5*ξопт)=0.35*(1-0,5*0.35)=0.2888 м2.
Высота ригеля: hр=h0+as=60.06+7=67.06 см.
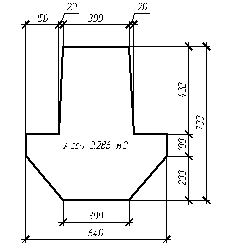
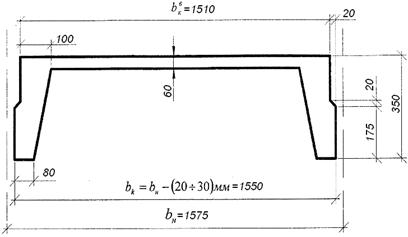
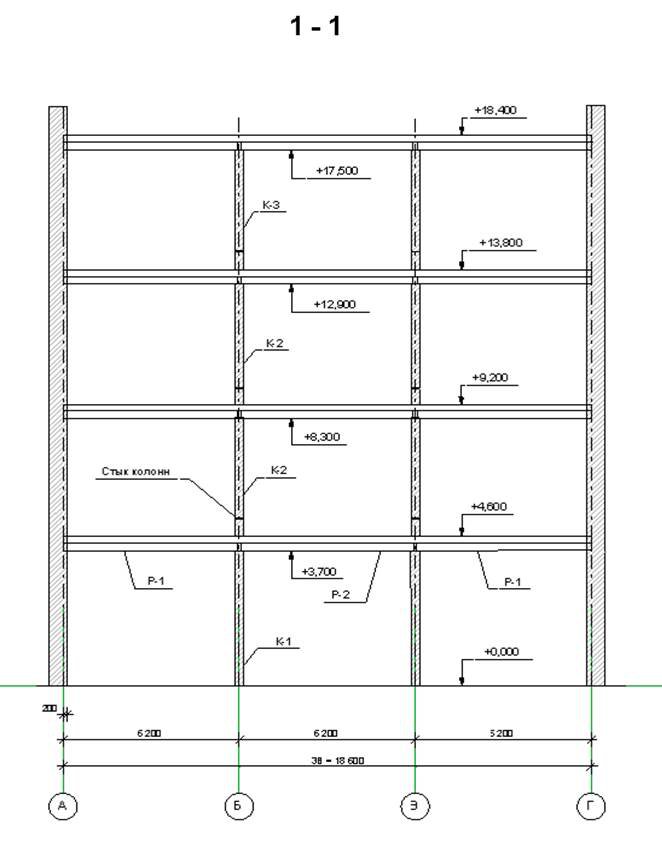
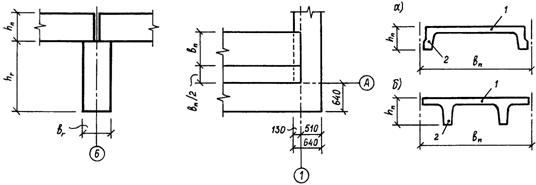
Принимаем ригель высотой hр=70 см и шириной bр=30 см из бетона класса B25 (Рис. 2.2.)
2. Определение размеров сечения колонн.
Нагрузка на среднюю и крайнюю колонны нижнего этажа:
Nср=Pпок*L+Pпер*L*(nэт-1)=44.564*6.4+126.428*6.4*(6-1)=4330.891 кН;
Nкр=Nср/2=4330.891/2=2165.445 кН.
Примем бетон средней колонны марки B30, с расчетным сопротивлением сжатию Rb=17 МПа, крайней – B30 (Rb=17 МПа) тогда требуемая площадь сечения средней и крайней колонн нижнего этажа:
Асртр=(1,1…1,5)*Nср/(γb2*Rb)=1.1*4330.891/0.9*17=3113.712 см2;
Акртр=(1,1…1,5)*Nкр/(γb2*Rb)=1.1*2165.445*10/0.9*17=1556.856 см2.
Задаемся шириной колонны bcol=40 см, тогда требуемая высота сечения колонн нижнего этажа:
hср сolтр=Асртр/bcol=3113.712/40=77.84 см;
hкр сolтр=Акртр/bcol=1556.856/40=38.92 см.
Учитывая, что кроме бетона нагрузку воспринимает арматура, примем следующие сечения колонн:
- средних – bср col*hср сol=400*600 мм из бетона класса B30.
- крайних – bкр col*hкр сol=400*400 мм из бетона класса B30.
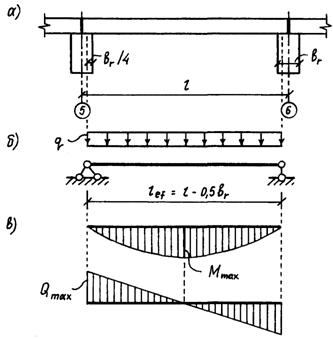
Расчетные пролеты ригелей (расстояния между осями колонн):
- в крайних пролетах l01=L-hкр сol/2=6400-400/2=6200 мм;
- в средних пролетах l02=L=6400 мм.
2.1.4 Определение жесткостей элементов рамыДлину стоек, вводимых в расчет, принимаем равной высоте этажа hэт=3.3 м.
Средняя расчетная длина ригелей:
l0=(l01+l02)/2=(6200+6400)/2=6300 мм=6.3 м.
Расстояние от центра тяжести сечения до нижней грани сечения ригеля:
y=S/Ap=0.090/0.286=0.3147 м,
где Ap=bp*hp=0.3*0.7=0.286 м2.
S=bp*hp2/2+2*0,02*hпл*0,5*(hp-hпл+hпл/3)+2*0,17*0,1*(hp-hпл-0,05)+2*0,17*(hp-hпл-0,1)2*0,5*2/3=0.3*0.72/2+2*0,02*0.4*0,5*(0.7-0.4+0.4/3)+2*0,17*0,1*(0.7-0.4-0,05)+2*0,17*(0.7-0.4-0,1)2*0,5*2/3=0.090 м3 –
статический момент относительно нижней грани сечения.
Определим жесткости ригеля (1), средних стоек (2) и крайних стоек (3), а также их соотношения.
1) Момент инерции сечения ригеля относительно центра тяжести:
Ip=bp*hp3/12+bp*hp*(hp/2-y)2=0.3*0.73/12+0.3*0.7*(0.7/2-0.3147)2=0.00884 м4.
Погонная жесткость ригеля (ригель из бетона класса B25, бетон подвергнут тепловой обработке, Eb=27000 МПа):
ip=Eb*Ip/l0=27*103*0.00884/6.3=37872 кН*м.
2) Момент инерции сечения средней стойки:
Iсрs3=bсрcol*hсрcol3/12=0.4*0.63/12=0.0072 м4.
Погонная жесткость средних стоек (колонна из бетона класса B30, бетон подвергнут тепловой обработке Eb=29000 МПа):
i3s=i’3s=Eb*Iсрs3/hэт=29000*103*0.0072/3.3=63273 кН*м.
Соотношение жесткостей:
η3=(i3s+1,5*i’3s)/ip=(63273+1,5*63273)/37872=4.177.
3) Момент инерции сечения крайней стойки:
Iкрs4=bкрcol*hкрcol3/12=0.4*0.43/12=0.00213 м4.
Погонная жесткость крайних стоек (колонна из бетона класса B30, бетон подвергнут тепловой обработке Eb=29000 МПа):
i4s=i’4s=Eb*Iкрs4/hэт=29000*103*0.00213/3.3=18747 кН*м.
Соотношение жесткостей:
η4=(i4s+1,5*i’4s)/ip=(18747+1,5*18747)/37872=1.238.
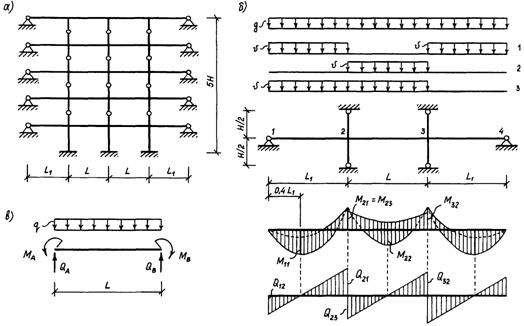
2.2 Расчетная схема и статический расчет поперечной рамыРасчетная схема поперечной рамы изображена на рис. 2.3.
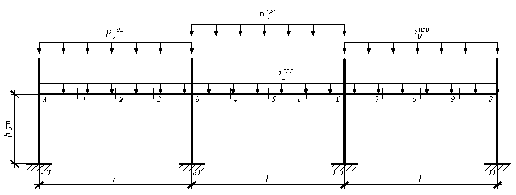
Статический расчет поперечной рамы проведем в программе RAMA2. Исходные данные для выполнения расчета сведены в таблицу 2.
Таблица 2. Исходные данные для программы RAMA2.| Величина | l01 | l02 | Pgпер | PVпер | η3 | η4 |
| Обозначение в программе | L01 | L02 | Pgпер | Pvпер | K1 | K2 |
| Значение | 6.2000 | 6.4000 | 30,6830 | 94.5400 | 4.1770 | 1.2380 |
╔═══════════════════════════════════════════════════════════════════════╗
║ Исходные данные ║
╠═══════════╦═══════════╦═══════════╦═══════════╦═══════════╦═══════════╣
║ L01 ║ L02 ║ Pgper ║ Pvper ║ K1 ║ K2 ║
║ [м] ║ [м] ║ [кН/м] ║ [кН/м] ║ ║ ║
╠═══════════╬═══════════╬═══════════╬═══════════╬═══════════╬═══════════╣
║ 6.2000║ 6.4000║ 30.6830║ 94.5400║ 4.1770║ 1.2380║
╚═══════════╩═══════════╩═══════════╩═══════════╩═══════════╩═══════════╝
╔═════════════════════════════════════════════════════════════════════╗
║ Изгибающие моменты в ригеле [кН/м] ║
╠═════╦═══════╦═══════╦═══════╦═══════╦═══════╦═══════╦═══════╦═══════╣
║ ║ M A ║ M1 ║ M2 ║ M3 ║ M BL ║ M BP ║ M4 ║ M5 ║
╠═════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╣
║ 1+2 ║-370.04║ 84.93║ 239.04║ 92.31║-355.27║-195.84║ -78.01║ -38.74║
╠═════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╣
║ 1+3 ║ -57.79║ 12.03║ 8.15║ -69.46║-220.78║-386.36║ 94.49║ 254.78║
╠═════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╣
║ 1+4 ║-307.31║ 95.20║ 196.87║ -2.31║-502.35║-497.22║ -16.36║ 143.93║
╚═════╩═══════╩═══════╩═══════╩═══════╩═══════╩═══════╩═══════╩═══════╝
╔═══════════════════════════════════════════════════════╗
║ Поперечные силы в ригеле [кН] ║
╠═════════════╦═════════════╦═════════════╦═════════════╣
║ Q A ║ Q BL ║ Q BP ║ Q CL ║
╠═════════════╬═════════════╬═════════════╬═════════════╣
║ 390.5728║ -385.8098║ 98.1856║ -98.1856║
╠═════════════╬═════════════╬═════════════╬═════════════╣
║ 68.8292║ -121.4054║ 400.7136║ -400.7136║
╠═════════════╬═════════════╬═════════════╬═════════════╣
║ 356.7342║ -356.7342║ 400.7136║ -400.7136║
╚═════════════╩═════════════╩═════════════╩═════════════╝
╔═══════════════════════════════════════════════════════════════════════╗
║ Изгибающие моменты в колоннах [кН/м] ║
╠═════╦══════════╦══════════╦══════════╦══════════╦══════════╦══════════╣
║ ║ M AB ║ M AH ║ M A0 ║ M BB ║ M BH ║ M B0 ║
╠═════╬══════════╬══════════╬══════════╬══════════╬══════════╬══════════╣
║ 1+2 ║ 148.0145║ -222.0217║ 111.0108║ -63.7738║ 95.6606║ -47.8303║
╠═════╬══════════╬══════════╬══════════╬══════════╬══════════╬══════════╣
║ 1+3 ║ 23.1171║ -34.6757║ 17.3379║ 66.2340║ -99.3509║ 49.6755║
╠═════╬══════════╬══════════╬══════════╬══════════╬══════════╬══════════╣
║ 1+4 ║ 122.9247║ -184.3871║ 92.1936║ -2.0516║ 3.0774║ -1.5387║
╚═════╩══════════╩══════════╩══════════╩══════════╩══════════╩══════════╝
Способ выравнивания – Луговой
╔══════════════════════════════════════════════════╗
║ Выравненные изгибающие моменты в ригеле [кН/м] ║
╠═════╦════════╦════════╦════════╦════════╦════════╣
║ ║ M A ║ M2 ║ M BL ║ M BP ║ M5 ║
╠═════╬════════╬════════╬════════╬════════╬════════╣
║ 1+2 ║ -370.04║ 239.04║ -355.27║ -195.84║ -38.74║
╠═════╬════════╬════════╬════════╬════════╬════════╣
║ 1+3 ║ -57.79║ 8.15║ -220.78║ -386.36║ 254.78║
╠═════╬════════╬════════╬════════╬════════╬════════╣
║ 1+4 ║ -307.31║ 254.86║ -386.36║ -386.36║ 199.35║
╚═════╩════════╩════════╩════════╩════════╩════════╝
2.3 Перераспределение усилий, построение огибающих эпюр
Рис. 2.4. Эпюры изгибающих моментов и поперечных сил в упругой стадии для различных комбинаций загружения ригелей.
Выравнивание для сочетания нагрузок 1+2.1) Условия MBL>MA, MBL>M2 не выполняются, перераспределение невозможно.
Выравнивание для сочетания нагрузок 1+3.1) ∆М=0.5*(MBP-М5)=0.5*(368.36-254.78)=56.79 кН*м.
2) 0,3*MBP=0,3*368.36=110.508 кН*м.
3) Принимаем ∆М=56.79 кН*м.
Выравнивание для сочетания нагрузок 1+4.Максимальный момент в Мmax=502.35 кН*м первом пролете.
Перераспределение начнем с первого пролета:
1) ∆М=0.75*(502.35-307.31)=146.28 кН*м.
2) 0,3*Мmax=0,3*502.35=150.705 кН*м.
3) Принимаем в первом пролете ∆М=146.28 кН*м.
4) Принимаем во втором пролете ∆М=141.15 кН*м.

Нагрузка от собственной массы крайней и средней колонн:
Nсcolкр=bcolкр*hcolкр*ΣHcol*ρcol*g*γf*γn=0.4*0.4*19.8*2.5*9,81*1.1*0.95=81.191 кН,
Nсcolср=bcolср*hcolср*ΣHcol*ρcol*g*γf*γn=0.4*0.6*19.8*2.5*9,81*1.1*0.95=121.787 кН,
где ΣHcol=hэт*nэт=3.3*6=19.8 м – суммарная высота колонны,
ρcol=2.5 т/м3 – плотность бетона колонны.
Нагрузка от остекления:
Nост=lост*ΣHост*ρост*γf*γn=5.8*7.2*0.4*1,1*0,95=17.456 кН,
lост=B=5.8 м – шаг рам,
ΣHост=1,2*nэт=1,2*6=7.2 м суммарная высота остекления,
ρост=0.4 кН/м2 – вес 1 м2 остекления.
Нагрузка от навесных стеновых панелей:
Nп=bп*lп*ΣHп*ρп*g*γf*γn=0.3*5.8*12.6*9,81*1*1,2*0,95=245.185 кН,
где bп=0.3 м – толщина стеновой панели,
lп=B=5.8 м – длина панели (шаг рам),
ΣHп=ΣHcol-ΣHост=19.8-7.2=12.6 м – суммарная высота стеновых панелей,
ρп=1 т/м3 – плотность бетона стеновой панели.
Суммарная нагрузка от навесных стеновых панелей и остекления:
Nст=Nп+Nост=245.185+17.456=252.385 кН.
Продольная сила, действующая соответственно на крайнюю и среднюю колонны:
Nкрcol=Nсcolкр+Pпок*l01/2+(nэт-1)*Pпер*l01/2+Nст=81.191+44.564*6.2/2+(6-1)*126.428*6.2/2+252.385=2431.352 кН,
Nсрcol=Nсcolср+Pпок*(l01+l02)/2+(nэт-1)*Pпер*(l01+l02)/2=
=121.787+44.564*(6.2+6.4)/2+(6-1)*126.428*(6.2+6.4)/2=4385.008 кН.
3 Проектирование панели перекрытия 3.1 Назначение размеров и выбор материалов. Сбор нагрузок на продольные ребра. Расчетная схема. Определение усилий
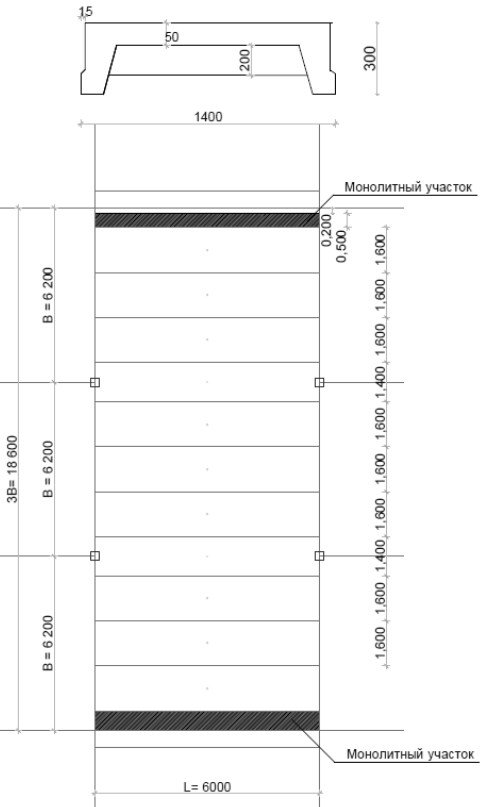
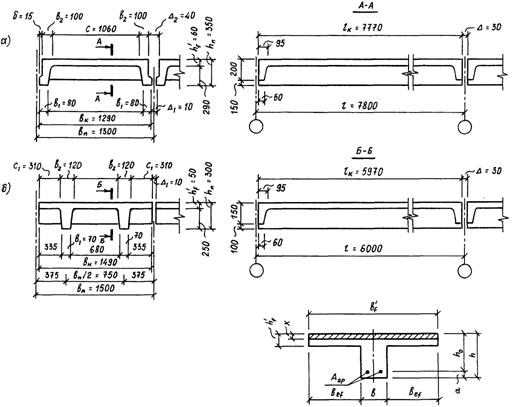
Проектируем ребристую панель перекрытия с предварительно напряженной арматурой.
Продольное ребро свободно опирается на ригель и рассматривается как балка, свободно опертая на двух опорах и загруженная равномерно распределенной нагрузкой.
Принимаем следующие размеры:
- зазор между гранью ригеля и торцом плиты принимаем d=30 мм;
- длина площадки опирания: lоп=100 мм;
- длина плиты lпл=B-bp-2*d-2*d=5800-300-2*30-2*20=5400 мм;
- высота продольного ребра – 400 мм;
- ширина продольного ребра внизу –70 мм;
- ширина продольного ребра вверху –100 мм;
- ширина поперечных ребер внизу – 50 мм;
- ширина поперечных ребер вверху – 70 мм;
- толщина полки hf’=50 мм.
- конструктивная ширина основной панели:
bf=(L-n*d)/n=(6400-4*30)/4=1570 мм,
где n=4 шт – количество плит в пролете,
d=30 мм – зазор между гранями продольных ребер панелей.
- номинальная ширина панелей:
а) основной bf’=bf+d=1600 мм,
б) доборной bf’доб=bf’/2=800 мм.
Материалы плиты:
- тяжелый бетон класса B25; γb2=0.9; Rb=14.5 МПа, Rbt=1.05 МПа, Rb,ser=18.5 МПа, Rbt,ser=1.6 МПа, Eb=27000 МПа, подвергнут тепловой обработке;
- напрягаемая арматура класса A800: Rs=680 МПа, Rs,ser=785 МПа, Es=190000 МПа;
- ненапрягаемая продольная арматура класса A400: 2 каркаса, диаметры ds=dsc=8 мм, As=Asc=100.5 мм2, Rs=Rsс=355 МПа, Rs,ser=390 МПа, Es=Esс=200000 МПа;
- ненапрягаемая поперечная арматура класса B500, Rsw=260 МПа, Rs,ser=395 МПа, Es=170000 МПа;
- полка панели армируется сетками из арматуры класса B500, Rs=260 МПа, Rs,ser=395 МПа, Es=170000 МПа.
Способ напряжения арматуры – электротермический на упоры формы.
Расчетный пролет панели:
lр=lпл-lоп=5400-100=5300 мм.
Полная нормативная погонная нагрузка на панель перекрытия:
Pn=gперn*bf’=18.214*1.6=29.142 кН/м.
Полная расчетная погонная нагрузка на панель перекрытия:
P=gпер*bf’=20.534*1.6=32.855 кН/м.
Временная расчетная погонная нагрузка на панель перекрытия:
Pv=ΣVпер*bf’=16.3*1.6=26.080 кН/м.
Максимальные усилия:
Мmax=P*lр2/8=32.855*5.32/8=115.361 кН*м;
Qmax=P*lр/2=32.855*5.3/2=87.065 кН.
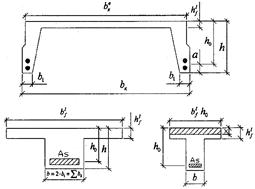
3.2 Расчет панели на прочность по нормальному сечениюВ расчет вводится приведенное тавровое сечение с полкой в сжатой зоне (Рис 3.2.).
Ширина полки приведенного таврового сечения bf’=1.6 м.
Толщина полки hf’=0.05 м.
Ширина ребра при расчете по предельным состояниям первой группы:
b1=2*bребниз+d=(2*70+30)/1000=0.17 м.
Ширина ребра при расчете по предельным состояниям второй группы:
b2=bребниз+bребвер+d=(70+100+30)/1000=0.2 м.
Высота таврового сечения h=0.4 м.
Расстояние от центра напрягаемой арматуры до нижней грани аsp=0.05 м.
Рабочая высота сечения h0=h-аsp=0.4-0.05=0.35 м.
Расчет ведем в предположении, что сжатой ненапрягаемой арматуры не требуется:
Rb*bf’*hf’*(h0-0.5*hf’)=14500*1.6*0.05*(0.35-0.5*0.05)=377 кН*м > Mmax=115.361 кН*м,
т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b=bf’=1.6 м.
Определим значение am:
am=Mmax/(Rb*b*h02)=115.361/(14500*1.6*0.352)=0.0406
Определим значение xR.
При подборе напрягаемой арматуры, когда неизвестно значение ssp, рекомендуется принимать σsp/Rs=0.6, тогда при классе арматуры A800 xR=0.41.
aR=xR*(1-xR/2)=0.41*(1-0.41/2)=0.326>am=0.0406,
т.е. сжатой арматуры действительно не требуется, тогда:
x=1-(1-2*am)0.5=1-(1-2*0.0406)0.5=0.041,
gs3=1,25-0,25*x/xR=1,25-0,25*0.041/0.41=1.22>1,1 => примем коэффициент условий работы gs3=1.1.
Тогда при Аs=100.5 мм2:
Asp=(x*Rb*b*h0-Rs*Аs)/(gs3*Rsp)=
=(0.041*14.5*1.6*0.35*106-355*100.5)/(1.1*680)=402.26 мм2.
Принимаем продольную напрягаемую арматуру: 2Æ18 A800 (Asp=508.9 мм2).
3.3 Вычисление геометрических характеристик приведенного сечения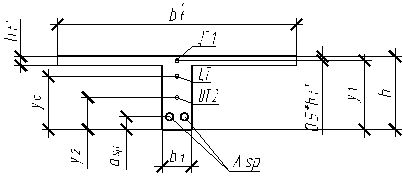
Ординаты центров тяжести:
y1=h-0.5*hf’=40-0.5*5=37.5 см;
y2=0.5*(h-hf’)=0.5*(40-5)=17.5 см.
Площадь приведенного сечения:
Ared=A+α*Asp=1395+7.037*5.089=1430.81 см2,
где A=A1+A2=800+595=1395 см2– площадь бетонной части поперечного сечения панели;
A1=hf’*bf’=5*160=800 см2;
A2=(h-hf’)*b1=(40-5)*17=595 см2;
a=Еs/Еb=190000/27000=7.037 – коэффициент приведения арматуры к бетону.
Статический момент площади сечения бетона относительно растянутой грани:
Sred=A1*y1+A2*y2+α*Asp*asp=800*37.5+595*17.5+7.037*5.089*5=40591.6 см3.
Расстояние от центра тяжести приведенного сечения до растянутой грани:
y0=Sred/Ared=40591.6/1430.81=28.37 см.
Момент инерции приведенного сечения относительно его центра тяжести:
Ired=I1+I2+α*Isp+A1*(y0-y1)2+A2*(y0-y2)2+α*Asp*(y0-аsp)2=
=bf’*(hf’)3/12+bf’*(h-hf’)3/12+α*π*dsp4/64+A1*(y0-y1)2+A2*(y0-y2)2+α*Asp*(y0-аsp)2=
=160*(5)3/12+160*(40-5)3/12+7.037*π*1.84/64+800*(28.37-37.5)2+595*(28.37-17.5)2+7.037*5.089*(28.37-5)2=729886.0 см4.
Момент сопротивления приведенного сечения по нижней и по верхней зонам:
Wred=Ired/y0=729886.0/28.37=25727.8 см3,
Wred’=Ired/(h-y0)=729886.0/(40-28.37)=62756.5 см3.
3.4 Определение потерь предварительного напряжения и усилия обжатияПредварительные напряжения без потерь ssp=0.9*Rsp.ser=0.9*785=706.5 МПа.
Первые потери:
1. Потери от релаксации напряжений арматуры при электротермическом способе натяжения для арматуры классов А800:
Dssp1=0,03*ssp=0,03*706.5=21.195 МПа.
2. Изделие при пропаривании нагревается вместе с формой и упорами, поэтому температурный перепад между ними равен нулю и, следовательно, Dssp2=0 МПа.
3. Потери от деформации стальной формы при электротермическом способе натяжения арматуры Dssp3=0 МПа.
4. Потери от деформации анкеров при электротермическом способе натяжения арматуры Dssp4=0 МПа.
Суммарные первые потери
Dssp(1)=Dssp1+Dssp2+Dssp3+Dssp4=21.195 МПа.
Усилие обжатия с учетом первых потерь:
P(1)=Asp*(ssp-Dssp(1))=508.9*(706.5-21.195)/103=348.78 кН.
Максимальное сжимающее напряжение бетона sbp от действия усилия P(1):
sbp=P(1)/Ared+P(1)*е0р1*уs/Ired=(348.78/1430.81+348.78*23.37*28.370/729886.0)*10=5.61 МПа < 0,7*Rb=10.15 МПа,
где e0p1=ysp=y0-аsp=28.37-5=23.37 см – эксцентриситет усилия Р(1) относительно центра тяжести приведенного сечения элемента,
уs=y0=28.370 см – расстояние от центра тяжести приведенного сечения до наиболее сжатой грани в стадии обжатия.
Вторые потери:
5. Потери от усадки бетона:
Dssp5=eb,sh*Es=0.0002*190000=38 МПа,
где eb,sh=0.0002 – деформация усадки бетона (для бетона класса B25).
6. Потери напряжений в напрягаемой арматуре от ползучести бетона:
Dssp6=0,8*jb,cr*a*sbp/[1+a*msp*(1+e0p1*asp*Аred/Ired)*(1+0.8*jb,cr)]=0,8*2.5*7.037*5.61/[1+7.037*msp*(1+23.37*5*1430.81/729886.0)*(1+0.8*2.5)]=64.89 МПа,
где jb,cr=2.5 – коэффициент ползучести бетона;
a=Еs/Еb=190000/27000=7.037 – коэффициент приведения арматуры к бетону;
msp=Аsp/А=5.089/1395=0.00365 – коэффициент армирования.
Суммарные вторые потери
Dssp(2)=Dssp5+Dssp6=38+64.89=102.89 МПа.
Общие потери
Dssp=Dssp(1)+Dssp(2)=21.195+102.89=124.09 МПа > 100 МПа =>
Dssp=124.09 МПа < 0.3*ssp=211.95 МПа =Dssp=124.09 МПа.
Напряжение с учетом всех потерь:
ssp2=ssp-Dssp=706.5-124.09=582.41 МПа.
Усилие обжатия от напрягаемой арматуры в растянутой зоне с учетом всех потерь напряжений:
Р=ssp2*Asp-Dssp(2)*As=582.41*508.9-102.89*100.5=286.07 кН.
3.5 Расчет панели на прочность по наклонному сечениюНаибольшая поперечная сила в опорном сечении: Qmax=87.065 кН.
Np=0,7*P=0,7*286.067=200.247 кН/м,
Nb=1,3*Rb*A1=1,3*14.5*68000=1281800 Н/м > Np=200.247 кН/м => Nb=1281.8 кН/м,
где A1=b1*h=170*400=68000 мм2 – площадь бетонного сечения без учета свесов сжатой полки.
Отношение Np/Nb=200.247/1281.8=0.156.
Определим коэффициент jn:
jn=1+3*Np/Nb-4*(Np/Nb)2=1+3*0.156-4*(0.156)2=1.371, тогда
Mb=1.5*jn*Rbt*b1*h02=1,5*1.371*1.05*170*0.352=44.97 кН*м.
q1=P-0,5*Pv=32.855-0,5*26.080=19.815 кН/м.
Qb1=2*(Mb*q1)0.5=2*(44.97*19.815)0.5=59.701 кН < 2*Mb/h0-Qmax=2*44.97/0.35-87.065=169.904 кН.
qsw=(Qmax-Qb1)/(1.5*h0)=(87.065-59.701)/(1.5*0.35)=52.121 кН/м.
jn*Rbt*b1*h0=1.371*1.05*170*0.35=85.66 кН.
Qb1=59.701 кН < jn*Rbt*b1*h0=1.371*1.05*170*0.35=85.66 кН. =>
при Qb1<jn*Rbt*b*h0 принимаем
qsw=(Qmax-Qb.min-3*h0*q1)/(1.5*h0)=(87.065-42.828-3*0.35*19.815)/(1.5*0.35)=44.631 кН/м, где
Qb,min=0,5*jn*Rbt*b*h0=0,5*1.371*1.05*170*0.35=42.828 кН.
Итак, qsw=44.631 кН/м.
qsw=44.631 кН/м < 0,25*jn*Rbt*b1=0,25*1.371*1.05*170=61.183 кН/м
Так как qsw<0,25*jn*Rbt*b тогда:
qsw=(Qmax/h0+8*q1)/1.5-[((Qmax/h0+8*q1)/1.5)2-(Qmax/(1.5*h0))2]0.5=
=(87.065/0.35+8*19.815)/1.5-[((87.065/0.35+8*19.815)/1.5)2-(87.065/(1.5*0.35))2]0.5=
=56.530 кН/м.
(Qmax/h0-3*q1)/3.5=(87.065/0.35-3*19.815)/3.5=54.089 кН/м.
qsw=56.530 кН/м >(Qmax/h0-3*q1)/3.5=54.089 кН/м => qsw=56.530 кН/м.
Окончательно получим qsw=56.530 кН/м.
Шаги хомутов у опоры S1 и в пролете S2 должны быть:
S1≤0,5*h0=0,5*350=175 мм,
S1≤300 мм,
S2≤0,75*350=0,75*350=262.5 мм,
S2≤500 мм.
Шаг хомутов, учитываемых в расчете, должен быть не более значения:
Sw.max=jn*Rbt*b1*h02/Qmax=1.371*1.05*170*0.352/87.065=344.3 мм.
Принимаем шаг хомутов у опоры S1=150 мм, в пролете S2=250 мм.
Требуемая площадь поперечной арматуры
Asw=qsw*S1/Rsw=56.530*150/260=32.61 мм2.
Принимаем в поперечном сечении 2 хомута диаметром 5 мм (Asw=39.3 мм2).
Фактические интенсивности усилий воспринимаемых хомутами у опоры и в пролете:
qsw1=Rsw*Asw/S1=260*39.3/150=68.068 кН/м;
qsw2=Rsw*Asw/S2=260*39.3/250=40.841 кН/м.
Определим длину участка с наибольшей интенсивностью хомутов qsw1.
Dqsw=0,75*(qsw1-qsw2)=0,75*(68.068-40.841)=20.420 кН/м > q1=19.815 кН/м.
Dqsw≥q1 =>
Длина участка с интенсивностью хомутов qsw1:
l1=(Qmax-(Qb.min+1.5*qsw2*h0))/q1-2*h0=(87.065-(42.828+1.5*40.841*0.35))/19.815-2*0.35=0.450 м,
где Qbmin=0,5*jn*Rbt*b1*h0=0,5*1.371*1.05*170*0.35=42.828 кН.
Принимаем длину приопорного участка с шагом хомутов S1 - l1=450 мм.
Количество шагов поперечной арматуры у опор
n1=l1/S1=450/150=3.00
Округляем количество шагов поперечной арматуры у опор n1у=4
Уточненная длина приопорного участка с шагом хомутов S1:
l1у=nу*S1=4*150=600 мм.
Примем выпуск продольной арматуры 25 мм, расстояние от края продольной арматуры до торца плиты понизу 150 мм, тогда суммарная длина приопорного участка с шагом хомутов S1 и выпуска продольной арматуры с расстоянием от края продольной арматуры до торца равно:
l1у/=600+25+150=775 мм.
Длина участка с шагом хомутов S2:
l2=lпл-2*l1у/=5400-2*775=3850 мм.
Количество шагов поперечной арматуры в середине ригеля:
n2=l2/S2=3850/250=15.4
Округляем количество шагов поперечной арматуры в середине ригеля n2у=15.
Уточненная длина приопорного участка с шагом хомутов S2:
l2у=nу2*S2=15*250=3750 мм.
Шаг доборных стержней S3=(lпл-2*l1у/-l2у)/2=(5500-2*2050-1400)=50 мм.

Нормативная длительно-действующая нагрузка:
Рnl=(gпер.n-Vпер.nкр)*bf’=(18.214-7)*1.6=17.942 кН/м.
Предельно-допустимый прогиб плиты:
fu=1/200*lp=1/200*5.3=0.0265 м.
Расчет производится на ЭВМ с помощью программы “PLITA”. Исходные данные для выполнения расчета сведены в таблицу 3.
Таблица 3. Исходные данные для программы PLITA.| N п/п | Исходная величина | Обозначение | Размерность | Значение |
| 1 | Масса 1 м2 плиты | gпл | кг | 275 |
| 2 | Расчетная погонная нагрузка | Р | кН/м | 32.855 |
| 3 | Нормативная погонная нагрузка | Рn | кН/м | 29.142 |
| 4 | Нормативная длительно-действующая нагрузка | Рnl | кН/м | 17.942 |
| 5 | Ширина ребра плиты | b | м | 0.2 |
| 6 | Ширина сжатой полки плиты | bf’ | м | 1.6 |
| 7 | Высота сжатой полки плиты | hf’ | м | 0.05 |
| 8 | Ширина растянутой полки плиты | bf | м | 0.2 |
| 9 | Высота растянутой полки плиты | bf | м | 0 |
| 10 | Высота плиты | h | м | 0.4 |
| 11 | Расчетный пролет плиты | lp | м | 5.3 |
| 12 | Длина площадки опирания плиты | Lоп | м | 0.1 |
| 13 | Расстояние от торца до места строповки петель | Lпет | м | 0,075 |
| 14 | Класс бетона | 25 | ||
| 15 | Передаточная прочность бетона | Rbp | МПа | 17.5 |
| 16 | Расчетное сопротивление напрягаемой арматуры | Rsp | МПа | 680 |
| 17 | Начальные напряжения в напрягаемой арматуре | σsp | МПа | 582.41 |
| 18 | Модуль упругости сжатой зоны | Es | МПа | 200000 |
| 19 | Модуль упругости напрягаемой арматуры | Esp | МПа | 190000 |
| 20 | Площадь сжатой арматуры | As’ | м2 | 0.0001005 |
| 21 | Площадь напрягаемой арматуры | Asp | м2 | 0.0005089 |
| 22 | Диаметр напрягаемой арматуры | D | мм | 18 |
| 23 | Расстояние от ц.т. сжатой арм. до верхней грани | А’ | м | 0.03 |
| 24 | Расстояние от центра тяжести напрягаемой арматуры до нижней грани плиты | а | м | 0.05 |
| 25 | Расстояние от центра тяжести нижнего ряда напрягаемой арматуры до нижней грани плиты | А1 | м | 0.05 |
| 26 | Предельно-допустимый прогиб плиты | fu, | м | 0.0265 |
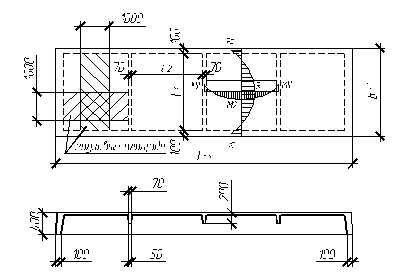
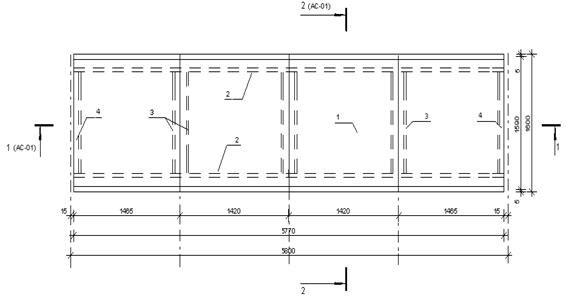
Рис. 3.4. Схема панели перекрытия
Определяем расчетный случай:
l1=bf’-2*100=1600-2*100=1400 мм;
l2=lпл/4-70=5400/4-70=1280 мм;
l1/l2=1400/1280=1.094<2; l2/l1=1280/1400=0.914<2; =>
полка работает как плита, опертая по контуру.
Таблица 4. Вычисление нагрузок на полку панели перекрытия.| №п/п | Наименование нагрузки | Нормативная нагрузка, кН/м2 | Коэффициент надежности по нагрузке, γf | Расчетная нагрузка, кН/м2 |
| 1 | 2 | 3 | 4 | 5 |
| ПЕРЕКРЫТИЕ | ||||
| I | ПОСТОЯННАЯ (gпер) | |||
| 1 | Керамические плитки ρ=1800 кг/м3, δ=13 мм 1800*0.013*9,81*0.95/1000 | 0.218 | 1.1 | 0.240 |
| 2 | Слой цементного раствора ρ=1800 кг/м3, δ=20 мм 1800*0.02*9,81*0.95/1000 | 0.336 | 1.3 | 0.436 |
| 3 | Выравнивающий слой из бетона ρ=2200 кг/м3, δ=20 мм 2200*0.02*9,81*0.95/1000 | 0.410 | 1.3 | 0.533 |
| 4 | Собственный вес полки ρ =2500 кг/м3; δ =50мм 2500*0,05*9,81*0,95/1000 | 1.1649 | 1.1 | 1.2814 |
| ИТОГО: ågпер=g1+g2+g3+g4 | 2.129 | 2.491 | ||
| II | ВРЕМЕННАЯ (Vпер) | |||
| 1 | Полезная (V1) а) кратковременная б) длительная | 14 7 7 | 1.2 1.05 | 8.4 7.35 |
| 2 | Перегородки (V2) | 0.5 | 1.1 | 0.55 |
| ИТОГО: åVпер=V1+V2 | 14.5 | 16.3 | ||
| ПОЛНАЯ: gпер=ågпер+åVпер | 16.629 | 18.791 |
Расчетная нагрузка на полосу шириной 1 м:
q=gпер*1=18.791*1=18.791 кН/м.
Изгибающие моменты в полке:
М1=МI=МI’=q*l12*(3*l2-l1)/[12*(4*l2+2.5*l1)]=
=18.791*1.42*(3*1.28-1.4)/[12*(4*1.28+2.5*1.4)]=0.869 кН*м;
МII=МII’=0,75*М1=0,75*0.869=0.652 кН*м;
М2=0,5*М1=0,5*0.869=0.434 кН*м.
Определяем площадь, подбираем диаметр и шаг рабочих стержней сетки в поперечном направлении:
А0=М1/(Rb*h02*100*γb2)=0.869*105/(14.5*352*100*0,9)=0.0489 м2.
где h0=h-as=50-15=35 мм.
Определяем h=0.9749.
Принимаем стержни из арматуры класса Вр500: Rs=360 МПа, Rsser=260 МПа, Es=170000 МПа.
Аs=М1/(Rs*h0*h)=0.869*106/(360*35*0.9749)=70.723 мм2.
Принимаем шаг стержней в поперечном направлении S1=200 мм, тогда количество рабочих стержней, приходящихся на расчетную полосу шириной 1 метр n1=1000/200+1=6;
Аs1=Аs/n1=70.723/6=11.787 мм2.
Принимаем Æ4 Вр500 (Аs1=12.566 мм2).
Аналогично определяем и шаг рабочих стержней в продольном направлении.
А0=МII/(Rb*h02*100*γb2)=0.652*105/(14.5*352*100*0,9)=0.0367 м2;
Определяем h=0.9812.
Аs=МII/(Rs*h0*h)=0.652*106/(360*35*0.9749)=52.700 мм2.
Принимаем шаг стержней в продольном направлении S2=200 мм, тогда n2=1000/200+1=6;
Аs2=Аs/n2=52.700/6=8.783 мм2.
Принимаем Æ4 Вр500 (Аs2=12.566 мм2).
Принимаем сетку С1 марки ![]() (Рис. 3.5.)
(Рис. 3.5.)
Для восприятия растягивающих напряжений от действия изгибающих моментов МI и МI’ вдоль продольных ребер укладываются сетки С1 марки ![]() с рабочими стержнями Æ4 Вр500 в поперечном направлении с шагом S=200 мм.
с рабочими стержнями Æ4 Вр500 в поперечном направлении с шагом S=200 мм.
Армирование поперечных ребер выполняется сварными каркасами КР2 с продольными стержнями диметром 8 мм из стали класса А400 с поперечными стержнями диаметром 4 мм из стали класса Вр500, устанавливаемыми с шагом S=200 мм.
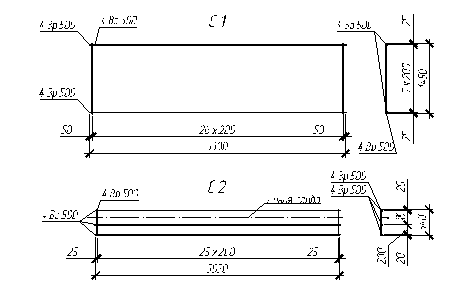
Рис. 3.5. Сварные сетки С1 и С2 для армирования полки панели.
4. Проектирование ригеля
4.1. Расчет прочности ригеля по нормальному сечению
Рассматривается ригель 1-ого пролета.
Ригель таврового сечения со свесами в растянутой зоне, с ненапрягаемой продольной рабочей арматурой (рис. 2.2.). Расчетное сечение ригеля – прямоугольное размерами: bр=300 мм, hр=700 мм. Площадь сечения консольных свесов в расчет не вводим, так как она вне сжатой зоны бетона.
Материалы ригеля:
- тяжелый бетон класса B25: gb2=0.9; Rb=14.5 МПа (с учётом gb2 Rb=13.05 МПа); Rbt=1.05 МПа (с учётом gb2 Rbt =0.945 МПа); Rb,ser=18.5 МПа; Rbt,ser=1.6 МПа; Eb=27000 МПа, бетон подвергнут тепловой обработке;
- ненапрягаемая продольная рабочая (пролетная и опорная), конструктивная и поперечная арматура класса A400:
а) диаметром 6 и 8 мм: Rs=355 МПа; Rs,ser=390 МПа; Rsw=285 МПа; Rsc=355 МПа; Es=200000 МПа,
б) диаметром от 10 до 40 мм: Rs=365 МПа; Rs,ser=390 МПа; Rsw=290 МПа; Rsc=355 МПа; Es=200000 МПа.
Целью расчета по нормальному сечению ригеля является определение диаметра и количества рабочей продольной арматуры в пролете ригеля и на его левой и правой опорах по грани колонн. Ригель перекрытия рассматривается как элемент поперечной многоэтажной рамы.
Пролетные и опорные изгибающие моменты принимаем в соответствии с огибающей эпюрой изгибающих моментов (рис. 2.5.).
СЕЧЕНИЕ В ПРОЛЕТЕ:
Расчетный момент: Мпр=245.63 кН*м.
h0=hр-as=700-50=650 мм – высота рабочей зоны.
αm=Mпр/(Rb*bр*h02)=245.63/(13.05*300*0.652)=0.148
ξr=0,8/(1+Rs/700)=0,8/(1+365/700)=0.526
αr=ξr*(1-0.5*ξr)=0.526*(1-0.5*0.526)=0.388
αm=0.148<αr=0.388.
Так как αm<αr, то сжатая арматура по расчету не требуется.
Требуемая площадь сечения растянутой арматуры:
As=Rb*bр*h0*[1-(1-2*αm)0.5]/Rs=13.05*300*0.65*[1-(1-2*0.148)0.5]/365=1126.3 мм2.
Принимаем в пролетном сечении (рис. 4.1. сечение 1-1):
- сжатую арматуру: 3Æ10 A400 (Asc=235.6 мм2) и 1Æ16 A400 (Asоп=201.1 мм2),
- растянутую арматуру: 6Æ16 A400 (Asпр=1206.4 мм2).
Коэффициент армирования:
μ=(As+Asc)/bр*h0=(1206.4+235.6)/300*650=0.0074
0.001<μ=0.0084<0.035.
СЕЧЕНИЕ НА ОПОРЕ:
Расчетный момент: Моп=370.04 кН*м.
h0=hр-asс=700-60=640 мм – высота рабочей зоны.
αm=Mоп/(Rb*bр*h02)=370.04/(13.05*300*0.642)=0.208
ξr=0,8/(1+Rs/700)=0,8/(1+365/700)=0.526
αr=ξr*(1-0.5*ξr)=0.526*(1-0.5*0.526)=0.388
αm=0.208<αr=0.388
Так как αm<αr, то сжатая арматура по расчету не требуется.
Требуемая площадь сечения растянутой арматуры:
As=Rb*bр*h0*[1-(1-2*αm)0.5]/Rs=13.05*300*0.64*[1-(1-2*0.208)0.5]/365=1795.4 мм2.
Принимаем в опорном сечении (рис. 4.1. сечение 2-2):
- сжатую арматуру: 3Æ16 A400 (Ascоп=603.2 мм2),
- растянутую арматуру: 1Æ16 A400, 2Æ32 A400 (Asоп=1809.6 мм2) и 3Æ10 A400 (Asc=235.6 мм2).
Коэффициент армирования:
μ=(As+Asc)/bр*h0=(4825.5+235.6)/300*640=0.0138
0.001<μ=0.0138<0.035.
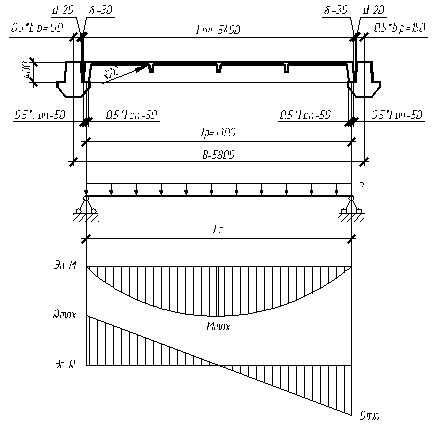
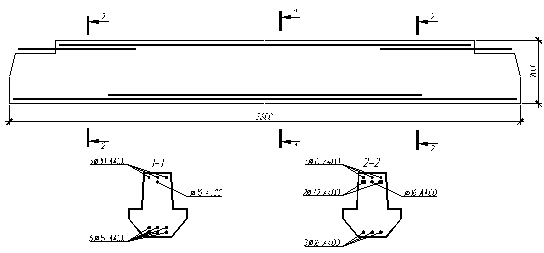 Рис. 4.1. Схема армирования ригеля продольной арматурой. 4.2 Расчет прочности ригеля по наклонному сечению
Рис. 4.1. Схема армирования ригеля продольной арматурой. 4.2 Расчет прочности ригеля по наклонному сечению Расчет ригеля по наклонному сечению производится с целью определения диаметра и шага поперечных стержней.
Длина ригеля 1-ого пролета:
lр=L-hкр сol-0.5*hср сol-2*∆=6400-400-0.5*600-2*50=5600 мм.
где ∆=50 мм – зазор между торцом ригеля и колонной.
Так как расчетное сечение ригеля прямоугольное jf=0.
Так как ригель изготавливается без преднапряжения jn=0.
j=1+jf+jn=1+0+0=1.
Наибольшая поперечная сила в опорном сечении: Qmax=390.53 кН.
Mb=1.5*j*Rbt*bр*h02=1,5*0.945*1*300*0.642=174.18 кН*м.
q1=Pпер-0,5*PVпер=126.428-0,5*94.540=79.158 кН/м.
Qb1=2*(Mb*q1)0.5=2*(174.18*79.158)0.5=234.843 кН > 2*Mb/h0-Qmax= 2*174.18/0.64-390.53=153.792 кН.
Интенсивности хомутов при Qb1≥2*Mb/h0-Qmax:
qsw=(Qmax2-Qb12)/(3*Mb)=(390.532-234.8432)/(3*174.18)=186.319 кН/м.
j*Rbt*bр*h0=0.945*1*300*0.64=181.44 кН.
Qb1=234.843 кН>j*Rbt*bр*h0=181.44кН =>
при Qb1>j*Rbt*bр*h0 принимаем qsw=186.319 кН/м.
qsw=186.319 кН/м > 0,25*j*Rbt*bр=0,25*0.945*300=70.875кН/м
Так как qsw>0,25*j*Rbt*bр, то примем qsw=186.319 кН/м.
Окончательно получим qsw=186.319 кН/м.
Задаемся шагом поперечных стержней.
Так как hр>450 мм, то на приопорных участках длиной l1=0,25*L=0,25*6400=1600 мм принимаем шаг S1 из условий:
S1≤hр/3=700/3=233.3 мм,
S1≤500 мм.
В средней части пролета назначаем шаг S2 из условий:
S2≤0,75*hр=0,75*700=525 мм,
S2≤500 мм.
Шаг хомутов, учитываемых в расчете, должен быть не более значения:
Sw.max=Rbt*bр*h02/Q=0.945*0.3*6402/390.53=297.3 мм
Принимаем шаг хомутов у опоры S1=200 мм, в пролете S2=500 мм.
Требуемая площадь одного поперечного стержня арматуры у опор:
Asw=qsw*S1/Rsw*n=186.319*200/285*3=43.583 мм2,
где n=3 шт - количество поперечных стержней в сечении у опор.
Диаметр одного поперечного стержня арматуры у опор назначаем по требуемой площади одного поперечного стержня и из условия свариваемости, диаметр одного поперечного стержня арматуры в пролете - из условия свариваемости:
dsw≥0.25*ds.max=0,25*32=8.0 мм.
Принимаем:
- в поперечном сечении у опор 3 стержня dsw1=8 мм (Asw1=150.8 мм2),
- в поперечном сечении в пролете 3 стержня dsw2=8 мм (Asw2=150.8 мм2).
Проверка прочности по наклонной полосе между наклонными трещинами.
Qmax=390.53 кН<0.3*Rb*b*h0=0.3*13.05*0.3*640=835.2 кН => прочность по наклонной полосе между наклонными трещинами обеспечена.
4.3 Построение эпюры материалов 4.3.1 Определение мест фактического обрыва нижних стержней
В целях экономии арматурной стали часть продольной рабочей арматуры обрывают в пролете, не доводя до опоры. Для определения мест обрыва строится эпюра материалов (арматуры). Места теоретического обрыва стержней определим графическим способом на огибающей эпюре изгибающих моментов (Рис. 4.2.).
Мsпр=Аsпр*Rs*u*h0*10-3=1206.4*365*0.922*0.65*10-3=263.93 кН*м,
где u=1-0,5*x=1-0,5*0.156=0.922;
x=Asпр*Rs/Rb*bр*h0=1206.4*365/13.05*300*650=0.156.
Продольные стержни доводимые за край опоры: 3Æ16 (Аs1=603.2 мм2).
Мs1=Аs1*Rs*u*h0*10-3=603.2*365*0.961*0.65*10-3=137.53 кН*м;
где u=1-0,5*x=1-0,5*0.078=0.961;
x=As1*Rs/Rb*bр*h0=603.2*365/13.05*300*650=0.078.
Определим расстояние от точек теоретического обрыва W из условий (здесь qsw=Asw*Rsw/S, ds- диаметр обрываемого стержня):
W≥Q/(2*qsw)+5*ds,
если Q/(2*qsw)>h0, то W≥2*h0*(1-qsw*h0/Q)+5*ds,
W кратно 50 мм.
1) qsw1=Asw1*Rsw/S1=150.8*285/200=214.885 кН/м,
Q1/(2*qsw1)+5*ds=170.89/(2*214.885)+5*16=477.6 мм.
2*h0*(1-qsw1*h0/Q1)+5*ds=2*650*(1-214.885*0.65/170.89)+5*16=317.5 мм.
Q1/(2*qsw1)=397.6<h0.
Принимаем W1=500 мм.
2) qsw2=Asw2*Rsw/S2=150.8*285/200=214.885 кН/м,
Q2/(2*qsw2)+5*ds.обр=168.58/(2*214.885)+5*16=472.3
2*h0*(1-qsw2*h0/Q2)+5*ds=2*650*(1-214.885*0.65/168.58)+5*16=302.9 мм.
Q2/(2*qsw2)=392.3<h0.
Принимаем W2=500 мм.
Длина обрываемых нижних стержней (в пролетной части ригеля):
lниз=l1Т+W1+W2=2750+500+500=3750 мм.
4.3.2 Определение мест фактического обрыва верхних стержнейМsоп=Аsоп*Rs*u*h0*10-3=2045.2*365*0.866*0.64*10-3=413.70 кН*м,
где u=1-0,5*x=1-0,5*0.268=0.866;
x=Asоп*Rs/Rb*bр*h0=2045.2*365/13.05*300*640=0.268.
Продольные стержни доводимые за край опоры 4 (Аs2=436.7 мм2).
Мs2=Аs2*Rs*u*h0*10-3=436.7*365*0.971*0.64*10-3=99.09 кН*м;
где u=1-0,5*x=1-0,5*0.057=0.971;
x=As2*Rs/Rb*bр*h0=436.7*365/13.05*300*640=0.057.
3) qsw3=Asw3*Rsw/S1=150.8*285/200=214.885 кН/м.
Q3/(2*qsw3)+5*ds.обр=296.15/(2*214.885)+5*0=689.1 мм.
2*h0*(1-qsw3*h0/Q3)+5*ds=2*640*(1-214.885*0.64/Q3)+5*0=685.6 мм.
Q3/(2*qsw3)>h0.
Принимаем W3=700 мм.
qsw4=Asw4*Rsw/S1=150.8*285/200=214.885 кН/м.
Q4/(2*qsw4)+5*ds.обр=243.89/(2*214.885)+5*0=567.5 мм.
2*h0*(1-qsw4*h0/Q4)+5*ds=2*640*(1-214.885*0.64/243.89)+5*0=558.2 мм.
Q4/(2*qsw4)<h0.
Принимаем W4=600 мм.
Длина обрываемых верхних стержней:
- со стороны крайней колонны
lверх кр=l2Т кр+W3=760+700=1460 мм, принимаем lверх кр=1800 мм.
- со стороны средней колонны
lверх ср=l2Т ср+W4=1200+600=1800 мм, принимаем lверх ср=1800 мм.
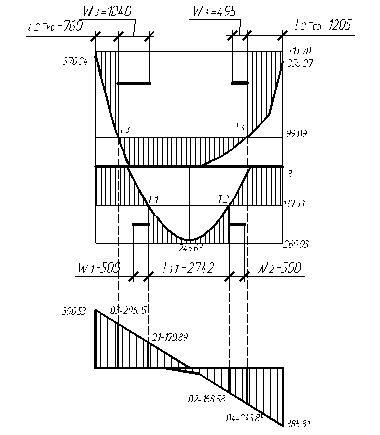 Рис. 4.2. Эпюра материалов.
Рис. 4.2. Эпюра материалов. 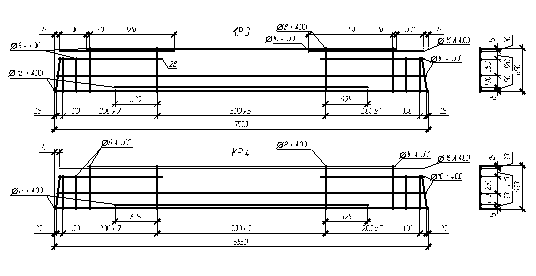
5 Проектирование колонны
5.1 Расчет колонны на устойчивость и прочность
Значение изгибающих моментов и продольных усилий принимается по результатам статического расчета поперечной рамы. Колонны принимаются двухэтажной разрезки. Колонны многоэтажного каркасного здания с жесткими узлами рассматриваются как элементы поперечной рамы и рассчитываются как внецентренно сжатые элементы от совместного действия изгибающих моментов и продольных сил.
Рассматривается нижняя колонна крайнего ряда сечением bcol*hсol=400*400 мм, изготавливаемая из тяжелого бетона класса B30: gb2=0.9; Rb=17 МПа; Rbt=1.2 МПа; (с учетом gb2 Rb=15.3 МПа; Rbt=1.08 МПа), Rb,ser=22 МПа; Rbt,ser=1.8 МПа; Eb=29000 МПа, бетон подвергнут тепловой обработке, и арматуры класса A400 Rsc=365 МПа, Rs=365 МПа, Es=200000 МПа.
Расчетная высота колонны принимается равной высоте этажа, т.е. l0=3.3 м.
Максимальный изгибающий момент в ригеле Mmax=370.04 кН*м, тогда получим одну комбинацию расчетных усилий в колонне:
М=0.6*Mmax=0.6*370.04=222.024 кН*м,
N=2431.352 кН.
e0=М/N=222.024/2431.352=0.0913 м.
Расчетные усилия от длительной нагрузки:
Мl=М*kl=222.024*0.591=131.199 кН*м,
Nl=N*kl=2431.352*0.591=1436.746 кН,
где kl=(gпер-8.4)/gпер=(20.534-8.4)/20.534=0.591.
М1=М+0,5*N*(h0-asс)=222.024+0,5*2431.352*(0.36-0.04)=611.040 кН*м.
M1l=Мl+0,5*Nl*(h0-asс)=131.199+0,5*1436.746*(0.36-0.04)=361.079 кН*м.
α=Es/Eb=200000/29000=6.897.
δe=e0/hcol=0.0913/0.4=0.228>0.15=> примем δe=0.228.
φl=1+M1l/M1=1+361.079/611.040=1.591.
В первом приближении принимаем коэффициент армирования μ=0.033.
Определим жесткость
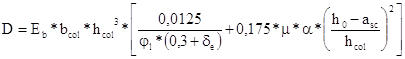 =
=
=29000*0.4*0.43*[0,0125/(1.591*(0,3+0.228))+
+0,175*0.033*6.897*((0.36-0.04)/0.4)2]=29.965 МПа*м4.
Ncr=π2*D/l02=π2*29.965/3.32=27157.190 кН.
ηv=1/(1-N/Ncr)=1/(1-2431.352/27157.190)=1.098
M=M*ηv=222.024*1.098=243.856 кН*м.
αm1=(M+N*(h0-asc)/2)/(Rb*b*h02)=
=(243.856+2431.352*(0.36-0.04)/2)/(15.3*103*0.4*0.362)=0.798
δ1=as/h0=0.04/0.36=0.111
αn=N/(Rb*bсоl*h0)=2431.352/(15.3*103*0.4*0.36)=1.104
ξR=0.531
αn=1.104>ξR=0.531
Расчет ведем для случая αn>ξR.
ξ1=(αn+ξR)/2=(1.104+0.531)/2=0.817
αs=(αm1-ξ1*(1-ξ1/2))/(1-δ1)=(0.111-0.817*(1-0.817/2))/(1-0.111)=0.354
![]() =(1.104*(1-0.531)+2*0.354*0.531)/(1-0.531+2*0.354)=0.759
=(1.104*(1-0.531)+2*0.354*0.531)/(1-0.531+2*0.354)=0.759
![]() =
=
=15.3*106*0.4*0.36*(0.111-0.759*(1-0.759/2))/(365*(1-0.111))=2220.0 мм2.
Принимаем продольную арматуру колонны 3Æ32 A400 (As=Asc=2412.7 мм2).
Конструктивные требования
Коэффициент армирования
μ1=(As+Asc)/(bcol*h0)=(2412.7+2412.7)/(400*360)=
0.03351
μ1>μmin=0.001
I(μ-μ1)/μI=I(0.033-0.03351)/0.033I=0.015<0,05
Диаметр поперечных стержней примем конструктивно из условий:
dsw≥0.25*dsmax(условие свариваемости),
dsw≥5 мм.
Максимальный диаметр dsmax=32 мм.
dsw≥0.25*32=8 мм.
Примем dsw=8 мм.
Шаг поперечных стержней примем конструктивно из условий:
S≤15*dsmax=15*32=480 мм,
S≤300 мм
Примем S=300 мм.
Принимаем поперечную арматуру колонны диметром dsw=8 мм, с шагом S=300 мм, из арматуры класса A400.
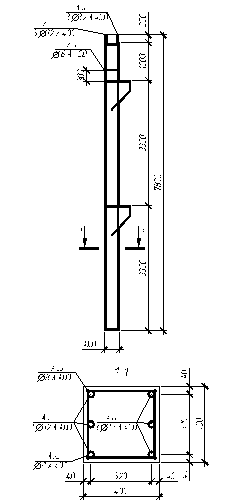
Рис. 5.1. Схема армирования колонны.
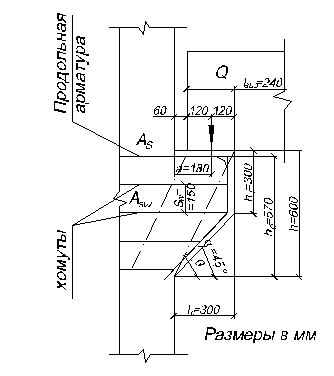
5.2 Расчет консоли колонныРассчитывается консоль колонны крайнего ряда.
Максимальная опорная реакция ригеля: Q=390.53 кН.
lsup=Q/(Rb*bp)=390.53/(15.3*0.3)=85.08 мм.
Принимаем вылет консоли l=300 мм.
a=l-0.5*lsup=300-0.5*85.08=257.5 мм.
Высота консоли в сечении у грани колонны h=600 мм.
Высота консоли у свободного края h1=300 мм.
Требуемая высота консоли у грани колонны:
h0≥Q/(2.5*Rbt*bcol)=390.53/(2.5*1.08*0.4)=361.6 мм.
Принимаем h0=h-as=600-50=550 мм.
Изгибающий момент в опорном сечении консоли:
M=1.25*Q*(l-Q/(2*Rb*bp))=1.25*390.53*(300-390.53/(2*15.3*0.3))=125.68 кН*м.
Требуемая площадь сечения арматуры класса A400:
As=M/(Rs*(h0-asc))=125.68/(365*(550-50))=688.7 мм2.
Принимаем 3Æ18 A400; (As=763.4 мм2).
Вычисляем параметры консоли:
tgθ=(h0-asc)/(a+0.5*lsup)=(550-50)/(257.5+0.5*85.08)=1.667
θ=59.04˚
sinθ=0.857
cosθ=0.514
Ширина наклонной полосы:
lb=lsup*sinθ+2*5*cosθ=85.08*0.857+2*5*0.514=78.1 мм.
h=600<2,5*257.5=2,5*27=644, консоль армируется только наклонными хомутами по всей высоте.
Суммарная площадь наклонных хомутов (отгибов):
Ainc=[Q/(0.8*Rb*bсol*lb*sinθ)-1]*bсol*Sinc/10*α=
=[390.53/(0.8*15.3*0.4*78.1*0.857)-1]*0.4*150/10*6.897=166.2 мм2,
где Sinc=150 мм – шаг отгибов:
Sinc£h/4=600/4=150 мм;
Sinc£150 мм.
α=6.897.
Ainc=0,002*bсol*h0=0,002*400*550=440 мм2.
Требуемая площадь сечения одного хомута
Ainc1=Ainc/2*n=440/2*3=73 мм2
где n=3 – число пар наклонных хомутов.
По сортаменту подбираем отгибы Æ10 A400 (Ainc1=78.5 мм2).
Горизонтальные хомуты принимаем по конструктивным требованиям: Æ8 A400 с шагом S=150 мм.
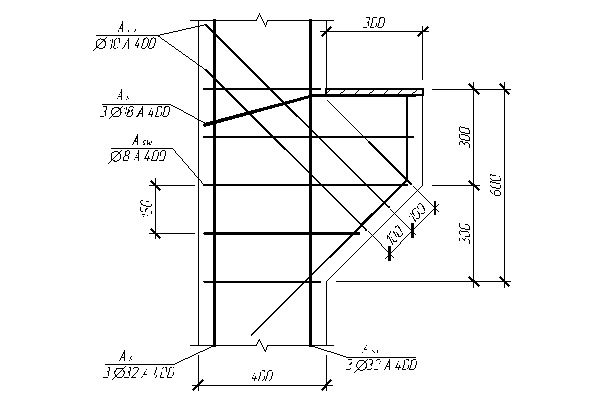 Рис. 5.2. Армирование консоли колонны.
Рис. 5.2. Армирование консоли колонны.
5.3 Расчет стыка ригеля с колонной
Максимальный опорный момент: Моп=370.04 кН*м.
Максимальная опорная реакция ригеля: Q=390.53 кН.
Требуемая площадь стыковых стержней колонны:
Askоп=Mвоп/(Rs*zs)=291.93/(365*590)=1355.6 мм2,
где Мвоп=Моп-Q*hcol/2=370.04-390.53*0.4/2=291.93 кН*м;
zs=h0-asс=640-50=590 мм.
Принимаем 2Æ32 A400 и Æ16 A400 (Аs=1809.6 мм2), т.к. диаметры стыковых стержней и выпусков арматуры ригеля одинаковы, то конструкция стыка является равнопрочной с сечением ригеля и не требует проверки расчетом.
Требуемая площадь сечения нижней опорной пластины ригеля (из стали марки C235 по ГОСТ 27772-88 Ry=230 МПа, Rwz=160 МПа):
Апл=N/Ry=494.80*10-3/230=2151.3 мм2;
где N=Мвоп/zs=291.93*106/590=494.80 кН.
Требуемая толщина пластины:
δпл=Апл/bp=2151.3/300=7.2 мм
δпл≥kf/1.2=9/1.2=7.5 мм,
где kf=9 мм – толщина катета шва.
Принимаем пластину сечением 300х8 мм.
Суммарная длина швов:
![]() =1,3*(494.80-58.58)/(0.85*9*160)=241.66 мм;
=1,3*(494.80-58.58)/(0.85*9*160)=241.66 мм;
F=Q*f=390.53*0.15=58.58 кН;
lw1=ålw1/2+10=241.66/2+10=241.66 мм – требуемая длина сварного шва с каждой стороны ригеля к стальной пластине колонны.
l=300 мм>lw1+∆=241.66+50=291.7 мм => величина вылета консоли достаточна.
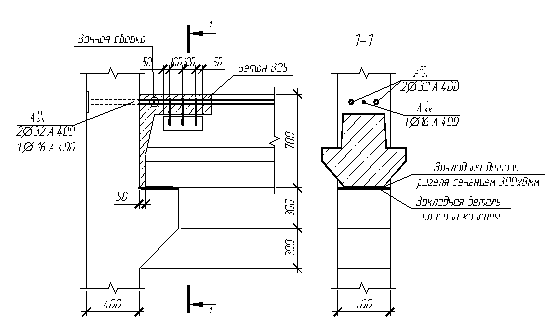
Рис. 5.3. Стык ригеля с колонной.
6 Проектирование монолитного перекрытия
6.1 Компоновка конструктивной схемы перекрытия из монолитного железобетона
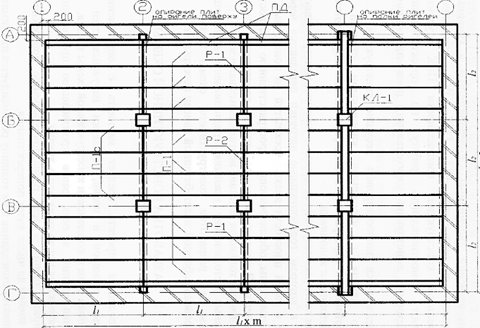
Монолитное перекрытие состоит из монолитной плиты, главных и второстепенных балок. Компоновка конструктивной схемы перекрытия с указанием элементов приведена на рис. 6.1.
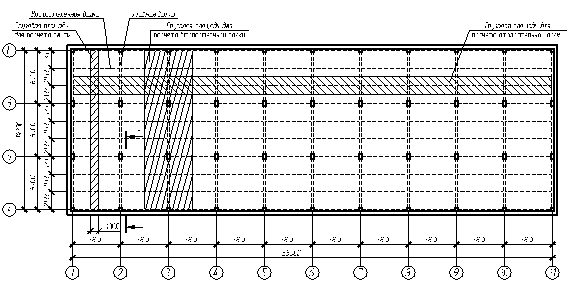 Рис. 6.1. Компоновка монолитного перекрытия. 6.2 Расчет и конструирование монолитной плиты
Рис. 6.1. Компоновка монолитного перекрытия. 6.2 Расчет и конструирование монолитной плиты 6.2.1 Определение шага второстепенных балок
Принимаем толщину монолитной плиты hпл=60 мм.
Расстояние между второстепенными балками из условия обеспечения жесткости:
L3≤40*hпл=40*60=2400 мм.
Минимальное количество шагов второстепенных балок в одном пролете:
n=L/40*hпл=6400/40*60=2.7, принимаем количество шагов n=3, тогда шаг второстепенных балок: L3=L/n=6400/3=2133 мм
6.2.2 Выбор материаловНазначаем для плиты тяжелый бетон класса B15: gb2=0.9; Rb=8.5 МПа; Rbt=0.75 МПа, (с учетом gb2 Rb=7.65 МПа; Rbt=0.675 МПа), Rbser=11 МПа, Rbtser=1.15 МПа, Eb=23000 МПа, бетон естественного твердения.
При армировании полки плиты раздельными плоскими сетками используется стержневая арматура класса A400: Rs=355 МПа, Rsw=285 МПа, Rsser=390 МПа, Es=200000 МПа.
Второстепенная балка армируется каркасами из арматуры класса A400: Rs=355 МПа, Rsw=285 МПа, Rsser=390 МПа, Es=200000 МПа.
6.2.3 Расчет и армирование плитыПлита рассчитывается на действие нагрузки на полосу шириной 1 м (рис. 6.1.). Расчетная схема плиты принимается как многопролетная неразрезная балка, опорами которой являются второстепенные балки. При вычислении нагрузок на 1 м2 перекрытия использованы результаты сбора нагрузок, приведенные в таблице 1.
Таблица 5. Вычисление нагрузок на перекрытие| №п/п | Наименование нагрузки | Нормативная нагрузка, кН/м2 | Коэффициент надежности по нагрузке, γf | Расчетная нагрузка, кН/м2 |
| 1 | 2 | 3 | 4 | 5 |
| ПЕРЕКРЫТИЕ | ||||
| I | ПОСТОЯННАЯ (gпер) | |||
| 1 | Собственный вес пола 0.218+0.336+0.410 | 0.964 | 1.3 | 1.115 |
| 2 | Собственный вес монолитной плиты 1×1×0.06×25×0,95 | 1.398 | 1.1 | 1.538 |
| ИТОГО: ågпер=g1+g2 | 2.362 | 2.652 | ||
| II | ВРЕМЕННАЯ (Vпер) | |||
| 1 | Полезная (V1) а) кратковременная б) длительная | 14 7 7 | 1.2 1.05 | 8.4 7.35 |
| 2 | Перегородки (V2) | 0.5 | 1.1 | 0.55 |
| ИТОГО: åVпер=V1+V2 | 14.5 | 16.3 | ||
| ПОЛНАЯ: gпер=ågпер+åVпер | 16.862 | 18.952 |
Предварительно назначаем высоту и ширину сечения второстепенной балки из условий:
hвб=(1/18…1/10)*L=(1/18…1/10)*6400=(355.6…640.0) мм,
принимаем hвб=550 мм.
Ширина второстепенной балки
bвб=(0.35…0,45)*hвб=(0.35…0,45)*550=192.5…247.5 мм,
принимаем bвб=200 мм.
Расчетный пролет плиты:
L03=L3-bвб=2133-200=1933 мм.
Выровненные изгибающие моменты:
- в средних пролетах и над средними опорами:
M2=q*L032/16=18.952*1.9332/16=4.43 кН*м/м.
- в первом пролете и на первой промежуточной опоре:
M1=q*L032/11=18.952*1.9332/11=6.44 кН*м/м.
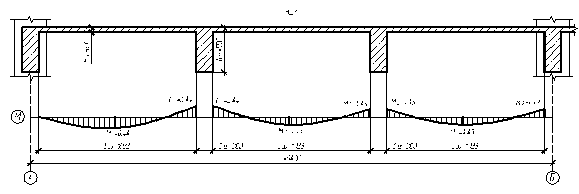 Рис. 6.2. Эпюра изгибающих моментов в плите.
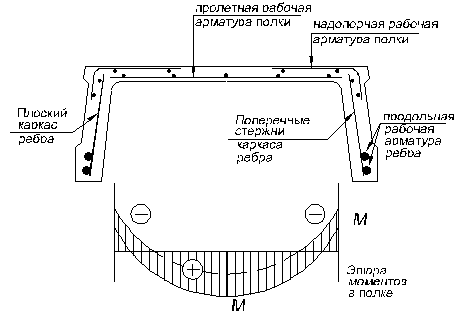
Рис. 6.2. Эпюра изгибающих моментов в плите. Монолитные плиты армируются раздельными плоскими сетками с поперечным расположением рабочей арматуры.
Принимаем защитный слой бетона a3=25 мм, расстояние от центра тяжести арматуры сеток до ближайшей грани сечения as=15 мм, тогда рабочая высота сечения ho=hпл-as=60-15=45 мм.
Ширина сеток:
С1 и С4 – BС1=BС4=L03=1933 мм, принимаем BС1=BС4=1900 мм.
С2 и С5 – BС2=BС5≥0,5*L03+bвб=0,5*1933+200=1166.7 мм,
принимаем BС2=BС5=1200 мм.
С3 – BС3≥=0,25*L03+bвб+15*d=0,25*1933+200+15*8=803.3 мм,
принимаем BС3=850 мм,
где: d=8 мм – диаметр поперечных стержней сеток принятый в первом приближении.
Длина здания:
Lзд=10*B=10*5800=58000 мм.
Длина сеток:
Lсет=Lзд-2*a3=58000-2*25=57950 мм.
Подбираем сетку С1:
αm=M1/gb2*Rb*b*h02=6.44/7.65*10000*0.0452=0.0416
ξ=0.042
η=0.979
As=M1/(Rs*h0*η)=6.44/(355*45*0.979)=411.9 мм2/м
Принимаем шаг поперечных стержней равным S=100 мм, тогда количество стержней в 1 м длины сетки равно n1=10.
Требуемая площадь сечения 1 стержня:
As1=As/n1=411.9/10=41.2 мм2.
Принимаем поперечные стержни Æ8 A400 (As1=50.3 мм2).
Сетка С1: ![]() .
.
Подбираем сетку С2: ![]() .
.
Параметры сетки С3 назначаются по конструктивным требованиям: ![]() .
.
Подбираем сетки С4 и С5:
αm=M2/gb2*Rb*b*h02=4.43/7.65*10000*0.0452=0.0286
ξ=0.029
η=0.985
As=M2/(Rs*h0*η)=4.43/(355*45*0.985)=283.2 мм2/м
Принимаем шаг продольных стержней равным S=150 мм, тогда количество стержней в 1 м ширины сетки равно n1=6.7.
Требуемая площадь сечения 1 стержня:
As1=As/n1=150/6.7=42.5 мм2.
Принимаем поперечные стержни Æ8 A400 (As1=50.3 мм2).
Сетка С4: ![]() .
.
Сетка С5: ![]() .
.
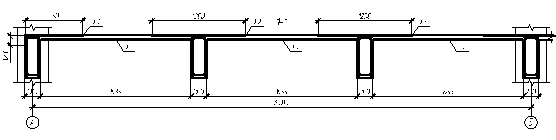 Рис. 6.3. Армирование плиты раздельными сетками. 6.3 Расчет по прочности второстепенной балки 6.3.1 Назначение размеров второстепенной балки и статический расчет
Рис. 6.3. Армирование плиты раздельными сетками. 6.3 Расчет по прочности второстепенной балки 6.3.1 Назначение размеров второстепенной балки и статический расчет Расчетный пролет второстепенной балки:
L01=B-brб=5800-220=5580 мм,
где brб=(0,3...0,4)*hrб – ширина сечения главной балки,
hrб=(1/12...1/10)*L=(1/10...1/12)*6400=533.3..640.0 мм.
принимаем hrб=600 мм., тогда brб=(0,3...0,4)*600=180..240 мм.
принимаем brб=220 мм.
Предварительные размеры второстепенной балки:
hвб=200 мм, bвб=550 мм.
Расчетная нагрузка на 1 п.м. балки:
qр=gпер*L3+bвб*(hвб-hпл)*rб*g*gfb*gn=
=18.952*2133*10-3+550*(550-60)*2500*9,81*0,95*1,1*10-9=42.9 кН/м.
Изгибаемые моменты:
М1=qр*L012/16=42.9*5.582/16=83.57 кН*м;
М2=qр*L012/11=42.9*5.582/11=121.55 кН*м;
М3=-a*qр*L012=-0.0529*42.9*5.582=70.67 кН*м.
Поперечные силы:
Q1=0,4*qр*L01=0,4*42.9*5.58=95.85 кН;
Q2=-0,6*qр*L01=-0,6*42.9*5.58=-143.77 кН;
Q3=±0,5*qр*L01=±0,5*42.9*5.58=±119.81 кН.
Далее уточняем размеры сечения второстепенной балки:
hовб=1,8*(М2/Rb*bвб)0,5=1,8*(121.55/8.5*550)0,5=0.481 м;
hвб=hовб+a3=481.3+50=531.3 мм.
Окончательно принимаем: hвб=550 мм; bвб=200 м.
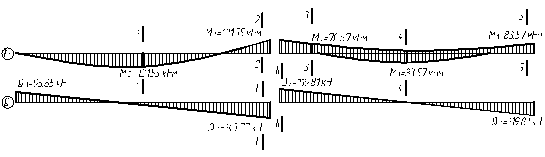 Рис. 6.4. Эпюра изгибающих моментов и перерезывающих сил во второстепенных балках. 6.3.. Расчет прочности второстепенных балок по нормальному сечению
Рис. 6.4. Эпюра изгибающих моментов и перерезывающих сил во второстепенных балках. 6.3.. Расчет прочности второстепенных балок по нормальному сечению Расчет по прочности второстепенной балки производится в пяти сечениях.
Балка в общем случае рассматривается как элемент таврового сечения с расчетным армированием растянутой зоны (x£xR). Уточняем размеры таврового сечения.
Так как hпл/hвб=60/550=0.11>0,1, величина свеса полки тавра определяется из условия:
bсв£1/6*L=1/6*6400=1067 мм,
bсв£L3-bвб=2133-200=967 мм.
Окончательно принимаем bсв кратно 50 мм в меньшую сторону bсв=950 мм.
Приведенная ширина полки:
b¢f=2*bсв+bвб=2*950+200=2100 мм.
Сечение 1-1
Сечение 1-1 рассматривается как тавровое сечение (учитывая знак действующего в сечении момента). Расчет производим в предположении, что сжатая арматура по расчету не требуется.
ho=hвб-as=550-50=500 мм.
Проверяем условие:
М2<Rb*b’f*h’f*(ho-0,5*h’f);
Rb*b’f*h’f*(ho-0,5*h’f)=8.5*2100*60*(500-0,5*60)=453.03 кН*м;
121.55 кН*м<453.03 кН*м - условие выполняется, т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b=b'f мм.
am=М2/Rb*b’f*h02=121.55/7.65*2100*5002=0.030<aR=0.39 т.е. сжатая арматура действительно по расчету не требуется.
Требуемая площадь сечения растянутой арматуры:
Аsтр=Rb*b’f*ho*[1-(1-2*am)0,5]/Rs=7.65*2100*500*[1-(1-2*0.030)0,5]/355=695.5 мм2.
Принимаем: 2Æ22 A400 (АS=760.3 мм2).
Сечение 4-4
Сечение 4-4 рассматривается как тавровое сечение (учитывая знак действующего в сечении момента). Расчет производим в предположении, что сжатая арматура по расчету не требуется.
Проверяется условие:
М1<Rb*b’f*h’f*(ho-0,5*h’f);
83.57 кН*м<453.03 кН*м - условие выполняется, т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b=b'f.
am=М1/Rb*b’f*h02=83.57/7.65*2100*5002=0.021<aR=0.39 т.е. сжатая арматура действительно по расчету не требуется.
Площадь сечения растянутой арматуры:
Аsтр=Rb*b’f*ho*[1-(1-2*am)0,5]/Rs=7.65*2100*500*[1-(1-2*0.021)0,5]/355=475.81 мм2
Принимаем: 2Æ18 А400 (АS=508.9 мм2).
Сечение 2-2
Сечение 2-2 проходит по грани главной балки, учитывая знак действующего в сечении момента, рассматривается как прямоугольное размерами bвб=200 мм, hвб=550 мм.
ho=hвб-asс=550-50=500 мм.
am=М2/Rb*bвб*ho2=121.55/7.65*200*5002=0.318
aR=0.39
Так как αm<αr, то сжатая арматура по расчету не требуется, примем её конструктивно: 2Æ12 A400 (АSС=226.2 мм2).
Требуемую площадь сечения растянутой арматуры:
As=Rb*bвб*h0*[1-(1-2*αm)0.5]/Rs=7.65*200*500*[1-(1-2*0.318)0.5]/355=854.1 мм2
Принимаем:
- сжатую арматуру: 2Æ12 A400 (АSС=226.2 мм2).
- растянутую арматуру: 2Æ25 A400 (As=981.7 мм2).
Сечение 5-5
Сечение проходит по грани главной балки, учитывая знак действующего в сечении момента, рассматривается как прямоугольное размерами bвб=200 мм, hвб=550 мм.
am=М1/Rb*bвб*h02=83.57/7.65*200*5002=0.218
aR=0.39
Так как αm<αr, то сжатая арматура по расчету не требуется, примем её конструктивно: 2Æ12 A400 (АSС=226.2 мм2).
Требуемую площадь сечения растянутой арматуры:
As=Rb*bвб*h0*[1-(1-2*αm)0.5]/Rs=7.65*200*500*[1-(1-2*0.218)0.5]/355=538.0 мм2
Принимаем:
- сжатую арматуру: 2Æ12 A400 (АSС=226.2 мм2).
- растянутую арматуру: 2Æ20 A400 (As=628.3 мм2).
Сечение 3-3
В сечении 3-3 проверяется прочность балки в точке теоретического обрыва рабочей арматуры. Расчет ведется для прямоугольного элемента с одиночной арматурой.
М3=70.668 кН*м.
hо.в.б.=500 мм.
x=Rs*As/(Rb*bвб)=355*981.7/(7.65*200)=227.8 мм.
Мcrc=7.65*200*227.8*(500-227.8/2)=134.6 кН*м.
Проверяем условие Мcrc³М3,
Похожие работы
... 20,66) · 100 = 314,57 · 105кН · м 5. Проектирование колонны первого этажа 5.1 Конструктивная схема Колонны многоэтажных промышленных зданий состоят из сборных ж/б элементов длиной, кроме элемента 1-го этажа, равной высоте этажа. Для опирания ригелей перекрытия колонны снабжены консолями. Стыки элементов колонн для удобства работ по соединению устраиваются на расстоянии 500—800 мм выше ...
... . 1). Размеры рядовой плиты 6,0 × 1,6 м. Таблица 1 Вид нагрузки Нормативная нагрузка (Н/м2) γf Расчетная нагрузка (Н/м2) 1.Постоянная: 1.1. Собств. Вес плиты 2000 1,1 2200 1.2. Конструкция пола 900 1,3 1170 Итого постоянная 2900 - 3370 2.Временная: 7000 1,2 8400 2.1. в т.ч. кратковременная 2000 1,2 2400 2.2. в т.ч. длительная 5000 1,2 ...
... стержней слева 2Ø28 А300: 504 мм < 20d = 560 мм справа 2Æ36 A-II (А300) 629 мм < 20d = 720 мм Принято W1= 500 мм; W2 = 550 мм; W3 = 600 мм; W4 = 750 мм. 6. Расчет сборной железобетонной колонны Сетка колонн м Высота этажей между отметками чистого пола – 3.3 м. Нормативное значение временной нагрузки на междуэтажные перекрытия 8.5 кH/м2, расчетное значение ...
... 1991. - 767 с. 7. Бондаренко В.М., Римшин В.И. Примеры расчёта железобетонных и каменных конструкций: Учеб. пособие. - М.: Высш. шк., 2006. - 504 с. 8. Тимофеев Н.А. Проектирование несущих железобетонных конструкций многоэтажного промышленного здания: Метод. указания к курсовой работе и практическим занятиям для студентов спец. "Строительство ж. д., путь и путевое хозяйство". - М.: МИИТ, 2004. ...
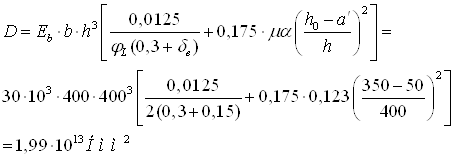
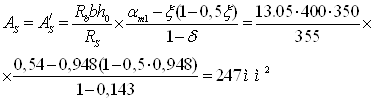
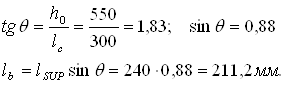

0 комментариев