Навигация
Динамический синтез систем автоматического управления
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Тема: "Динамический синтез систем автоматического управления"
Введение
Существует чрезвычайно большое разнообразие автоматических систем, выполняющих те или иные функции по управлению самыми различными физическими процессами во всех областях техники.
В данной курсовой работе производится динамический синтез следящей системы автоматического управления.
В следящей системе выходная величина воспроизводит изменение входной величины, причем автоматическое устройство реагирует на рассогласование между выходной и входной величинами. Следящая система имеет обратную связь выхода со входом, которая по сути дела, служит для измерения результата действия системы. На входе системы производится вычитание входного сигнала и сигнала с датчика обратной связи. Величина рассогласования воздействует на промежуточные устройства, а через нее на управляемый объект. Система работает так, чтобы все время сводить к нулю рассогласование.
В состав системы входят нелинейности, именно поэтому по характеру внутренних динамических процессов ее относят к нелинейным системам. По протеканию процессов в системе ее относят к непрерывным, т. к. в каждом из звеньев непрерывному изменению входной величины во времени соответствует непрерывное изменение выходной величины.
Для того чтобы линеаризованная система отвечала требуемым показателям качества в установившемся режиме и переходном процессе, она подвергается синтезу, а именно, в нее включается регулятор, который реализует выбранный закон управления. В интересах простоты расчета сводим задачу к такой форме, чтобы максимально использовать методы исследования обыкновенных линейных систем, т. к. теория и различные прикладные методы для них наиболее полно разработаны.
1. Синтез линейной системы 1.1 Анализ исходной системы
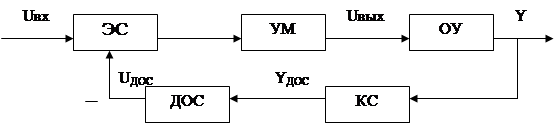
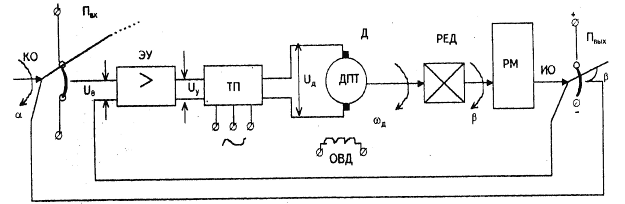
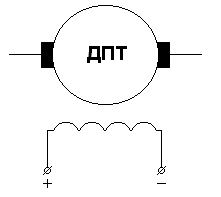
Рисунок 1.1 Функциональная схема замкнутой системы,
где
ЭС - элемент сравнения;
УМ – усилитель мощности;
ОУ – объект управления;
КС – кинематическая связь;
ДОС – датчик обратной связи;
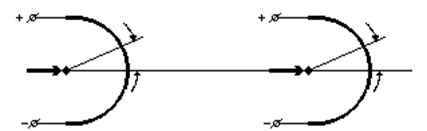
Усилитель мощности предполагается безынерционным, но с ограниченной зоной линейности ±UВХmax. В кинематической связи между ОУ и ДОС присутствует люфт (зазор) величиной 2D (рис. 1.2.).
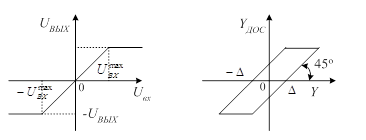
Рисунок 1.2. – Нелинейные характеристики элементов
Передаточные функции ОУ и ДОС известны:
![]() ,
,
где ![]()
![]() ,
,
где ![]()
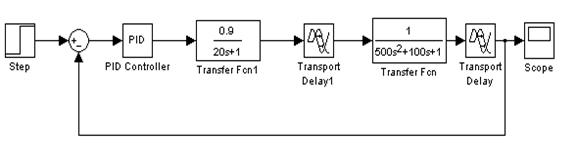
Составим структурную схему исходной системы:
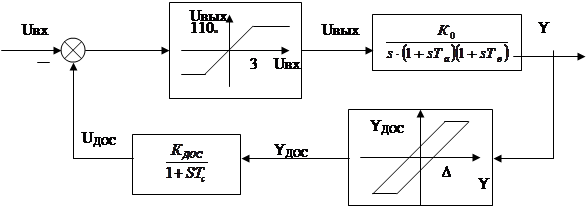
Рисунок 1.3 Структурная схема исходной системы
Для линеаризации системы пренебрегаем наличием нелинейных эффектов, то есть, считаем, что:
- усилитель мощности имеет неограниченную зону линейности
- зазор (люфт) в кинематической связи "выход системы – датчик обратной связи" отсутствует и коэффициент передачи равен единице
Усилитель мощности, имея неограниченную зону линейности, будет иметь передаточную функцию вида:
![]() ,
,
где КУМ – коэффициент передачи УМ.
Максимально выходное напряжение усилителя 110В, а зона нелинейности усилителя мощности по входу ±3В.
![]()
Тогда получим следующую структурную схему линеаризованной системы.
|  | |||||||
|
| |||||||
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
Рисунок 1.4 Структурная схема линеаризованной системы
По критерию Гурвица проверим устойчивость замкнутой системы.
Передаточная функция замкнутой системы имеет вид:
![]()
![]()
![]() (1.1)
(1.1)
Запишем характеристическое уравнение замкнутой системы:
![]()
![]()
Необходимым условием устойчивости системы является одинаковость знака всех коэффициентов. Данное условие выполняется. Достаточным условием является положительность определителей Гурвица. Т.к. система 4 порядка, то следует проверить знак ∆3.
![]()
![]()
![]() (В)
(В)
Следовательно, замкнутая система устойчива.
Проверим, удовлетворяет ли система требованиям ТЗ.
Т.к. в ТЗ оговариваются только максимальная скорость νmax и максимальное ускорение εmax, то следует перейти к эквивалентному гармоническому сигналу вида:
![]()
![]()
![]() с-1
с-1
![]()
![]()
Амплитуду ошибки найдем по модулю передаточной функции по ошибке.
![]() ,
,
![]() ,
,
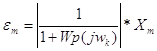
где ![]() - частотная передаточная функция разомкнутой системы.
- частотная передаточная функция разомкнутой системы.
Так как ![]() , то справедливо соотношение
, то справедливо соотношение ![]() .
.
Поэтому ![]()
![]()
Тогда, модуль частотной передаточной функции:
![]() (1.2)
(1.2)
Относительную динамическую ошибку системы определим по формуле:
![]()
Подставляя значение ωk в формулу, получим ![]()
Тогда находим ![]()
Относительная динамическая ошибка системы 25,4%, следовательно, система не удовлетворяет требованиям ТЗ.
Проверим, удовлетворяет ли система требованиям ТЗ в переходном режиме, т.е. ![]()
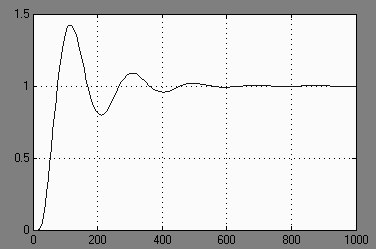
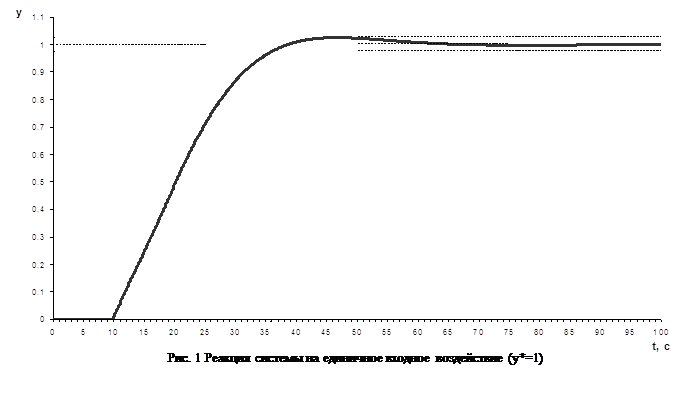
Для этого нужно построить график переходной характеристики по выходу ДОС.
![]()
![]()
Для построения используем программный пакет MathCad
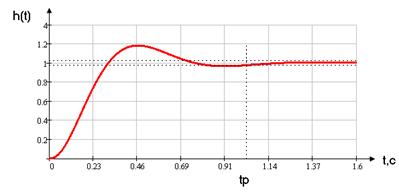
Рисунок 1.5 Переходная характеристика по выходу ДОС
Для определения перерегулирования (s) воспользуемся формулой:
![]()
![]()
Тогда ![]()
Т.е. получили, что перерегулирование удовлетворяет требованиям ТЗ.
Теперь найдем время регулирования (tp). Для этого строим “коридор”, равный ±0,022![]()
Из рисунка видно, что tp=1,04с
Т.е. время регулирования не удовлетворяет требованиям ТЗ и данную систему следует откорректировать.
Похожие работы
... регулятор на нелинейный элемент. В качестве нелинейного элемента возьмём идеальное реле, статическая характеристика звена изображена на рисунке 23. Рис.23. Идеальное реле Чтобы реализовать данный регулятор в заданной системе автоматического управления, требуется рассчитать значения параметра с. Проанализируем работу системы с нелинейной характеристикой и без неё в Simulink, а затем найдём ...
... ) формирования регулятором регулирующих воздействий в частности, как задача коррекции в нужном направлении динамических свойств регулятора. При этом рассмотрение схем систем автоматического регулирования производится как на основании структурных соображений, т.е. исходя из характера взаимодействия отдельных элементом системы, определяемых лишь видом математического описания этих элементов, так и в ...
... определению: ; Составим диагональные миноры: ; ; Итак, получаем, что ; ; , т.е. условие устойчивости системы не выполняется, а следовательно система по критерию Гурвица неустойчива. 4.2 Исследование устойчивости САУ по критерию Найквиста В соответствии со структурной схемой (рис.3) АЧХ и ФЧХ разомкнутой САУ можно представить в виде произведения АЧХ и суммы ФЧХ элементарных ...
... записи в Zam_ck=inv(l+sysl)*sysl можно в диалоговом режиме произвести новую запись zpk(.) - сокращая одинаковые элементы числителя и знаменателя в Zam_ck. 2.Исследование линейной импульсной системы автоматического управления Задание: 1) Найти передаточные функции импульсной САУ: W*(z) разомкнутой системы, Ф*(z) – замкнутой системы, Фе*(z) – системы по ошибке. Параметры Т, Т1, τ1, К0, ...

0 комментариев