Навигация
Анализ системы с пропорциональным регулятором
1.2 Анализ системы с пропорциональным регулятором
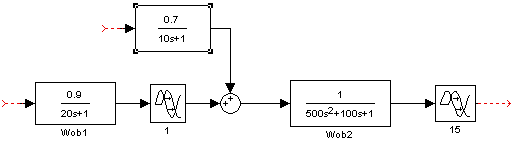
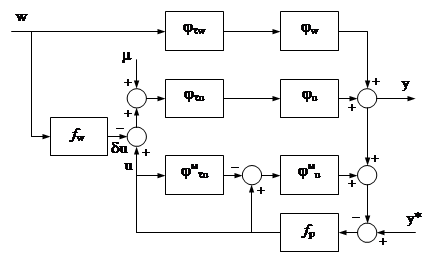
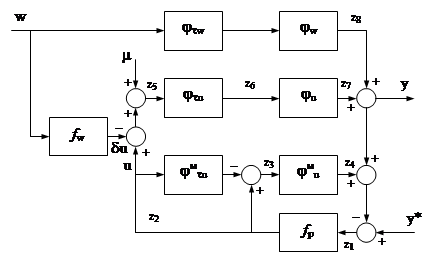
1.2.1 Структурная схема линеаризованной системы с пропорциональным регуляторомПропорциональный регулятор реализует простейший линейный закон управления, при котором управляющий сигнал, подаваемый на вход объекта управления, представляет собой усиленный по величине и по мощности сигнал ошибки (рассогласования). В системах с невысокими требованиями такой закон иногда может обеспечить приемлемое качество регулирования и всегда полезно узнать, не относится ли к ним и наша система.
Cоставим структурную схему с пропорциональным регулятором:

Рисунок 1.6 Структурная схема с пропорциональным регулятором
В установившемся режиме заданную точность обеспечивает низкочастотный участок. Проще всего оценить точность системы по ее реакции на гармонический входной сигнал.
![]() ,
,
Из пункта 1.1 ![]()
Для того, чтобы входное воздействие воспроизводилось с ошибкой, не превышающей em, ЛАХ системы должна проходить не ниже контрольной точки Ak c координатами:
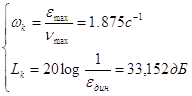
(1.3)
Построим запретную область (ЗО)
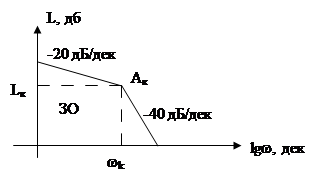
Рисунок 1.7 Запретная область
Определим минимальный коэффициент усиления разомкнутой системы [1, § 12.6]с пропорциональным регулятором, учитывая
![]() , где εm– относительная ошибка системы
, где εm– относительная ошибка системы
![]() с-1
с-1
Отсюда, коэффициент усиления пропорционального регулятора:
![]()
1.2.2 Проверка устойчивости замкнутой системы
Для проверки устойчивости замкнутой системы воспользуемся алгебраическим критерием Гурвица. [1, § 6.2]
Запишем характеристическое уравнение системы:
![]()
Т.к. система 4 порядка, то достаточно определить D3
![]()
![]()
Т.к. определитель больше нуля и все коэффициенты положительны, то замкнутая система с пропорциональным регулятором устойчива.
Теперь проверим систему по критерию Найквиста: [1, § 6.5] анализируем разомкнутую систему, а вывод делаем об устойчивости замкнутой системы.
Передаточная функция разомкнутой системы имеет вид:

Запишем характеристическое уравнение разомкнутой системы:
![]()
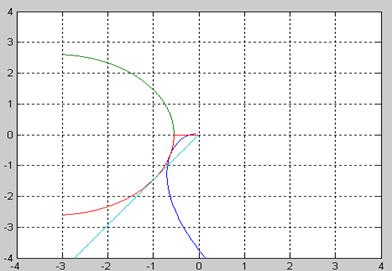
Все корни характеристического уравнения левые, кроме одного нулевого. Если разомкнутая система на границе устойчивости, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал особую точку с координатами (-1;j0).
![]()
Выделим действительную и мнимую часть:
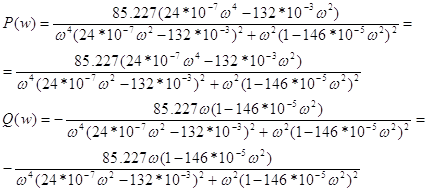
(1.5)
Будем изменять значения w от 0 до ¥ и находить соответствующие значения Р и Q.
Таблица 1.1
| w | P | Q |
| 0 | -11.25 | -¥ |
| 234.5 | 0 | 4,584*10-3 |
| 26.2 | -0.95 | 0 |
| ¥ | 0 | 0 |

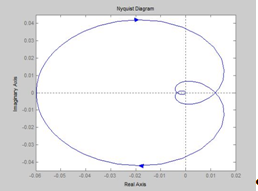
Рисунок 1.8 Годограф Найквиста
Из рисунка видно, что замкнутая система устойчива.
Проверим устойчивость замкнутой системы по логарифмическим частотным характеристикам.
Построим логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ).
[1, § 4.4]
Определим модуль частотной передаточной функции для разомкнутой системы:
![]() ;
;
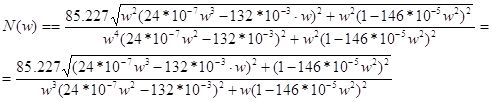 (1.7)
(1.7)
Определим L(w) и ![]()
![]() ;
;
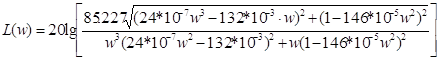 ;
;
![]()
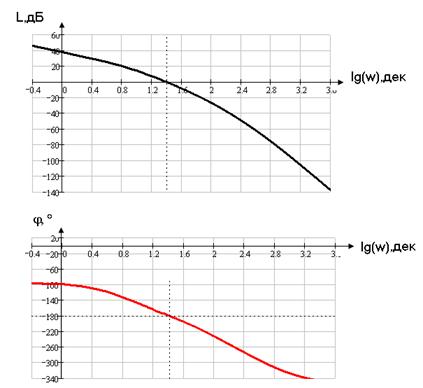
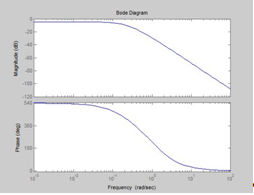
Рисунок 1.9 ЛАЧХ и ЛФЧХ системы с регулятором
Видно, что точка пересечения ЛФЧХ с линией -180о лежит немного правее точки пересечения ЛАЧХ с осью абсцисс. Следовательно, замкнутая система устойчива.
Проверим систему на устойчивость по критерию Михайлова. [1, § 6.3]
Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова начинался на вещественной положительной полуоси и при увеличении частоты последовательно проходил число четвертей, соответствующее порядку системы (нигде не обращаясь в 0).
Функция Михайлова для нашей системы:
![]()
Выделим вещественную и мнимую части:
![]() ;
;
![]()
Построим годограф Михайлова по следующим значениям:
Таблица 1.2
| w, | X(w) | Y(w) |
| 0 | 85,227 | 0 |
| 25,6 | 0 | 1,105 |
| 26,2 | -4,252 | 0 |
| 233,1 | 0 | -1,8259∙104 |
|
| ∞ | -∞ |
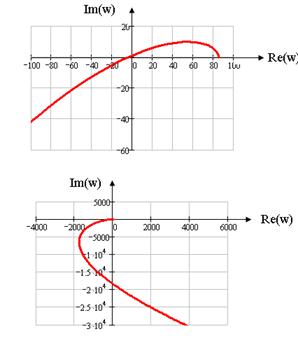
Рисунок 1.10 Годограф Михайлова для малых и больших частот соответственно
Следовательно, система устойчива.
Частота среза разомкнутой и замкнутой системы, запасы устойчивости, критический коэффициент усиления, прямые показатели качества и косвенный показатель качестваЧастота среза – это частота, в которой ЛАЧХ системы пересекает ось абсцисс. Определим ее по графику ЛАЧХ (рисунок 1.9):
L(w)=0 при w=25.59 c-1
Критическая частота(wkp) – частота, при которой фазовая характеристика пересекает уровень -1800.
wkp=1,418 с-1
Запасы устойчивости определим по формулам:
![]() – запас устойчивости по амплитуде,
– запас устойчивости по амплитуде,
![]() –запас устойчивости по фазе
–запас устойчивости по фазе
Получаем:
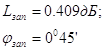
Определим критический коэффициент усиления системы Kkp по критерию Михайлова.
Критический коэффициент усиления – такое значение Kp, при котором замкнутая система находится на границе устойчивости.
Если система находится на границе устойчивости, то левая часть характеристического уравнения равна 0.
![]()
Откуда вытекают два равенства:
![]()
Следовательно, годограф Михайлова должен проходить через начало координат.
Запишем функцию Михайлова:
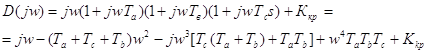
Выделим вещественную и мнимую части и приравняем их к нулю:
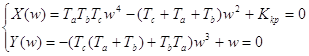 ;
;
Из уравнения Y(w)=0 находим w:
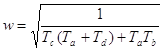
Подставляем это значение в уравнение X(w)=0 и находим критический коэффициент усиления Kkp
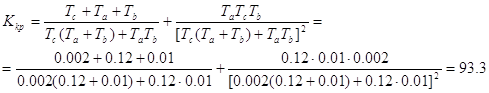
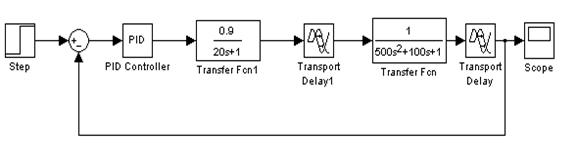
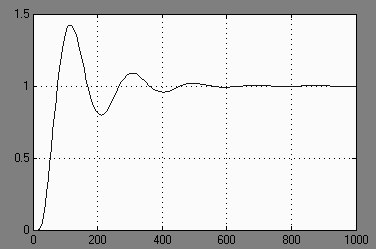
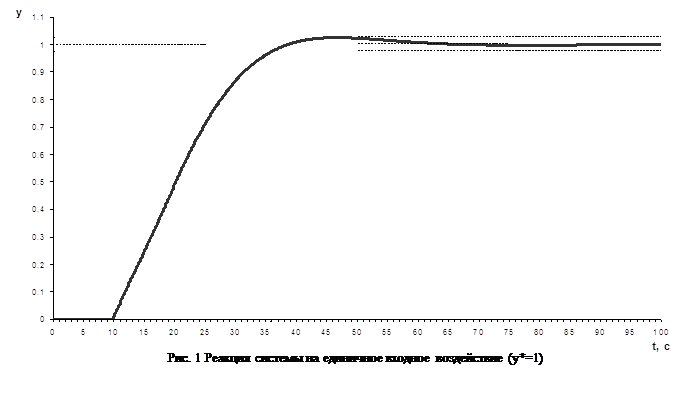
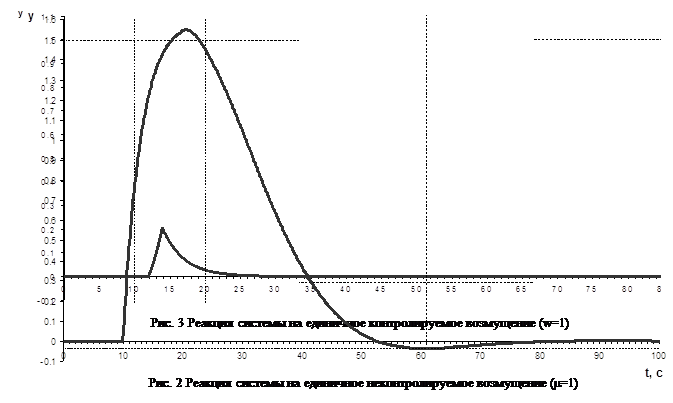
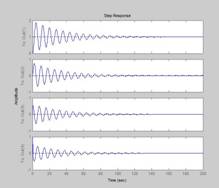
Прямые показатели качества системы ![]() и tpопределим по графику переходной характеристики замкнутой системы с пропорциональным регулятором по выходу ДОС. [приложение 2]
и tpопределим по графику переходной характеристики замкнутой системы с пропорциональным регулятором по выходу ДОС. [приложение 2]

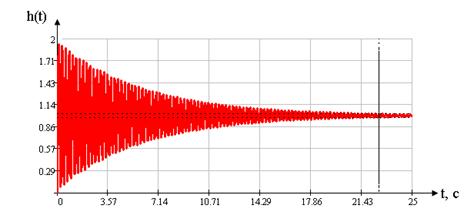
Рисунок 1.11 График переходной характеристики замкнутой системы по выходу ДОС
По графику находим:
hmax=1,95
![]() = 1
= 1
Найдем перерегулирование ![]()
Для определения tp построим “коридор” равный ![]() .
.
tp=22,72 с.
Показатель колебательности определяется по АЧХ замкнутой системы.
Запишем передаточную функцию замкнутой системы по выходу ДОС
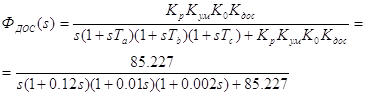 (1.8)
(1.8)
Преобразуем и выделим вещественную и мнимую части:
![]() ;
;
![]() .
.
Запишем модуль частотной передаточной функции по выходу ДОС:
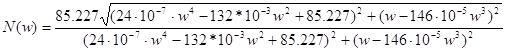 (1.9)
(1.9)
По формуле (1.9) построим АЧХ замкнутой системы
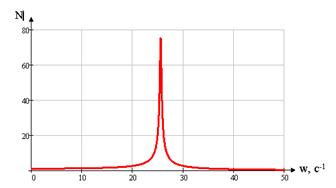
Рисунок 1.12 АЧХ замкнутой системы по выходу ДОС
Показатель колебательности определим по формуле:
![]() ,
,
где ![]() максимальное значение ординаты АЧХ замкнутой системы по выходу ДОС;
максимальное значение ординаты АЧХ замкнутой системы по выходу ДОС;
N(0) – значение ординаты АЧХ при w=0.
По рисунку определяем:
![]() ; N(0)=1;
; N(0)=1;
Откуда находим: M=75,214
Анализ на соответствие системы с пропорциональным регулятором требованиям ТЗПроверим систему на требования по точности воспроизведения входного сигнала.
Относительную динамическую ошибку системы определим по формуле:
![]()
![]() ;
; ![]()
Передаточная функция разомкнутой системы:
![]()
Тогда, модуль частотной передаточной функции:

Подставляя значение ωkв формулу для ![]() , находим
, находим ![]()
Относительная динамическая ошибка системы 2,5%, следовательно, система не удовлетворяет требованиям ТЗ.
Время переходного процесса tp=22,72 с. и перерегулирование![]() , найденные ранее, не удовлетворяют требованиям ТЗ.
, найденные ранее, не удовлетворяют требованиям ТЗ.
При введении пропорционального регулятора прямые показатели качества не удовлетворяют требуемым.
При введении регулятора увеличился коэффициент усиления разомкнутой системы и время регулирования. Хотя величина ошибки уменьшилась, тем не менее, она не удовлетворяет требованиям ТЗ. В результате введения регулятора качество переходного процесса ухудшилось.
1.3 Синтез регулятора Описание методики синтеза регулятора для одноконтурной следящей системы
Динамический синтез – направленный расчет, имеющий конечной целью отыскание рациональной структуры системы и установление оптимальных величин параметров отдельных ее элементов.
Более узкая цель синтеза – определение вида и параметров корректирующего устройства, которое нужно добавить к некоторой неизменяемой части системы, чтобы обеспечит требуемое качество системы в установившемся и переходном режимах.
Наиболее приемлемым для решения задачи динамического синтеза является метод логарифмических амплитудных характеристик (метод ЛАХ). [1, § 12.5] Стадии синтеза по методу ЛАХ включают:
1. построение располагаемой ЛАХ, т.е. ЛАХ исходной системы
2. построение желаемой ЛАХ системы, удовлетворяющей требованиям ТЗ
3. определение вида и параметров корректирующего устройства
4. проверочный расчет – моделирование СУ, позволяющее убедиться в том, что спроектированная система удовлетворяет всем требованиям ТЗ.
Построение исходной ЛАХПередаточная функция исходной разомкнутой системы:
![]() ;
;
Построим исходную асимптотическую ЛАХ.
![]()
![]() lg(wа)=0,921;
lg(wа)=0,921;
![]() lg(wв)=2;
lg(wв)=2;
![]() lg(wс)=2,699
lg(wс)=2,699
На оси lgw отмечаем lg–ы частот сопряжений. Проводим низкочастотную асимптоту с наклоном -20дБ/дек до первой частоты сопряжения wa. Эта асимптота пересекает ось L в точке ![]() . На частоте сопряжения эта асимптота изменяет наклон до -40дБ/дек и проводится до wв. На частоте wв изменяем наклон до -60дБ/дек и проводим асимптоту до wс. На частоте wс меняем наклон до -80 дБ/дек и проводим асимптоту.
. На частоте сопряжения эта асимптота изменяет наклон до -40дБ/дек и проводится до wв. На частоте wв изменяем наклон до -60дБ/дек и проводим асимптоту до wс. На частоте wс меняем наклон до -80 дБ/дек и проводим асимптоту.
Построенная исходная асимптотическая ЛАХ представлена на миллиметровке.
Построение желаемой ЛАХЖелаемую ЛАХ условно разбивают на 3 участка:
1 участок – низкочастотный. Он отвечает за обеспечение требуемой точности системы в установившемся режиме. Чем в большем диапазоне частот он расположен, тем в большем диапазоне частот не происходит заметного ослабления входного сигнала.
2 участок – среднечастотный. Он отвечает за устойчивость и качество системы в переходном режиме (оценивается величиной запасов устойчивости, прямыми показателями качества - s, tр, косвенным показателем М). Этот участок характеризуется 2 параметрами: частотой среза wср и наклоном асимптоты, проходящей через частоту среза.
![]()
Традиционно наклон асимптоты берется равным -20дБ/дек, поскольку, чем больше наклон асимптоты, тем труднее обеспечить хорошие динамические свойства системы.
Похожие работы
... регулятор на нелинейный элемент. В качестве нелинейного элемента возьмём идеальное реле, статическая характеристика звена изображена на рисунке 23. Рис.23. Идеальное реле Чтобы реализовать данный регулятор в заданной системе автоматического управления, требуется рассчитать значения параметра с. Проанализируем работу системы с нелинейной характеристикой и без неё в Simulink, а затем найдём ...
... ) формирования регулятором регулирующих воздействий в частности, как задача коррекции в нужном направлении динамических свойств регулятора. При этом рассмотрение схем систем автоматического регулирования производится как на основании структурных соображений, т.е. исходя из характера взаимодействия отдельных элементом системы, определяемых лишь видом математического описания этих элементов, так и в ...
... определению: ; Составим диагональные миноры: ; ; Итак, получаем, что ; ; , т.е. условие устойчивости системы не выполняется, а следовательно система по критерию Гурвица неустойчива. 4.2 Исследование устойчивости САУ по критерию Найквиста В соответствии со структурной схемой (рис.3) АЧХ и ФЧХ разомкнутой САУ можно представить в виде произведения АЧХ и суммы ФЧХ элементарных ...
... записи в Zam_ck=inv(l+sysl)*sysl можно в диалоговом режиме произвести новую запись zpk(.) - сокращая одинаковые элементы числителя и знаменателя в Zam_ck. 2.Исследование линейной импульсной системы автоматического управления Задание: 1) Найти передаточные функции импульсной САУ: W*(z) разомкнутой системы, Ф*(z) – замкнутой системы, Фе*(z) – системы по ошибке. Параметры Т, Т1, τ1, К0, ...

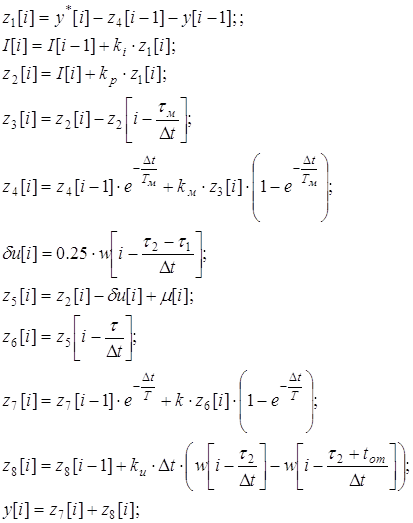
0 комментариев