Дослідження властивостей лiнiйних динамічних кіл

Вступ

В даній курсовій роботі ми розглянемо перетворення сигналів довільної форми лінійними динамічними колами першого порядку в часовій та частотній областях. В часовій області ми розглянемо визначення перехідної характеристики кола (класичним або операторним методами) та реакції кола на сигнал довільної форми методом інтеграла згортки (Дюамеля). В частотній області за допомогою комплексно-частотної функції кола дослідимо основні частотні характеристики (АЧХ, ФЧХ, характеристику групового часу запізнення), визначимо граничні частоти та смугу пропускання.

Метою роботи є освоєння різних методів, для знаходження реакції кола на вхідний сигнал довільної форми, та переконання на практиці, що при використанні, ці методи є ефективними та правильними.

При дослідженні характеру зміни основних частотних характеристик в залежності від зміни параметрів елементів кола проводиться якісний та кількісний аналізи процесів ,що відбуваються в колі в залежності від частоти вхідного сигналу. Визначається амплітудний та фазовий спектри вхідного сигналу та реакція на його дію.

Для наочності та зручності результати обчислень представляються в табличній та графічній формах. Таблиці та графіки наведені в курсовій роботі побудовані за допомогою пакету програм Mathcad 2003.

1. Визначення реакції кола на вхідний сигнал довільної форми методом інтеграла Дюамеля (інтеграла згортки)

Метод інтеграла Дюамеля відноситься до класу методів аналізу динамічних систем у часовій області, коли як діючий сигнал, так і властивості системи описуються функцією часу.

В основі цього методу лежать два так звані принципи:

• принцип розкладання довільного сигналу на суму так званих елементарних сигналів, яка з деякою точністю відповідає початковому сигналу;

• принцип суперпозиції: реакція лінійного кола на довільну дію є алгебраїчною сумою реакцій на окремі компоненти.

Найбільше поширення в теорії електричних кіл при розкладенні довільного сигналу мають одиничний ступінчастий σ(t) та одиничний імпульсний δ(t). Розкладання сигналу у цьому базисі є різновидом динамічного зображення довільного сигналу. Реакція на такі елементарні сигнали визначається часовими характеристиками: перехідною h(t) та імпульсною g(t) і має вигляд:

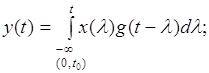 (1.1)

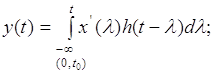 (1.2)

де x(t) - діючий сигнал.

Визначимо перехідну характеристику для нашого кола за допомогою операторного методу.

Так як реакція кола – напруга на виході i_вих (елемент навантаження R1), то будемо шукати операторну функцію як передаточну провідність – Y_пер(р). Для цього побудуємо операторну схему заміщення кола (рис. 1.1, а).

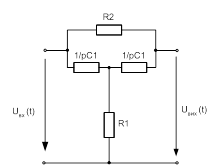
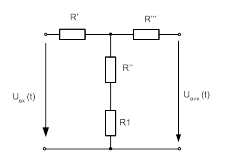
Рисунок 1.1 – Схема заміщення електричного кола

Перетворимо трикутник 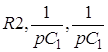 в зірку: ;

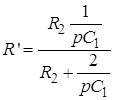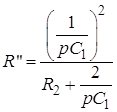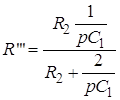;  (рис. 1.1, б). Через елемент струм не протікає, тому, оскільки у нас нульові початкові умови, за правилом свого плеча:

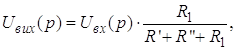
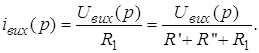 (1.3)

Тоді:

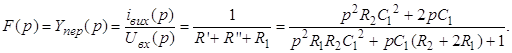 (1.4)

Або:

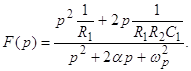
Звідси маємо зображення перехідної характеристики:

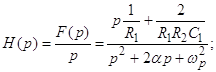 (1.5)

Де 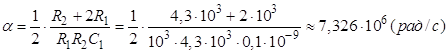– коефіцієнт згасання кола,  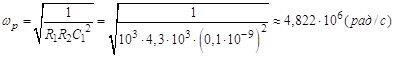– частота резонансу контуру, 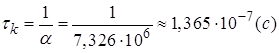– постійна часу кола.

Оскільки , тому перехідний процес, а отже і перехідна характеристика, повинні мати аперіодичний характер.

Переходячи від зображення (1.5) до оригіналу перехідної характеристики маємо:

 (1.6)

де , ,

, .

Імпульсна характеристика як похідна по часу від перехідної:

 (1.7)

Графік перехідної характеристики показано на рис 1.2,а; імпульсної – на рис 1.2,б. Результати розрахунків  і  вказані в таблиці 1.1.

Таблиця 1.1 Значення перехідної та імпульсної характеристик

0	10	-9.965
3,00000	4.216	-3.03
6,00000	2.37	-1.059
9,00000	1.658	-0.475
12,0000	1.295	-0.283
15,0000	1.056	-0.205
18,0000	0.874	-0.162
21,0000	0.728	-0.133
24,0000	0.607	-0.11
27,0000	0.506	-0.092
30,0000	0.422	-0.076

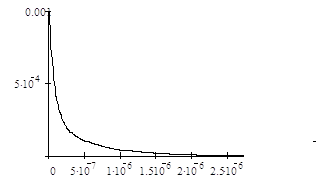
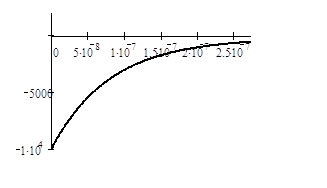
Рисунок 1.2 – Перехідна (а) та імпульсна (б) характеристики

Тепер знайдемо реакцію на сигнал довільної форми (рис. А.2).

Ураховуючи те, що діючий сигнал має різні функціональні залежності від часу на різних часових відрізках, визначимо реакцію на цей сигнал методом припасовування.

Розглянемо проміжок часу , де .

На цьому проміжку вхідний сигнал: .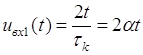

Згідно з методом перехідних характеристик реакція має вигляд:

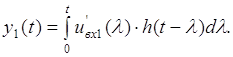
Далі розглянемо проміжок часу , де .

На цьому проміжку математична модель вхідного сигналу має вигляд:

.

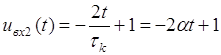Тоді реакція, знайдена за інтегралом Дюамеля, має вигляд:

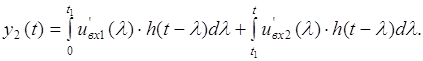
На проміжку часу  вхідний сигнал: .

Тоді реакція, знайдена за інтегралом Дюамеля, має вигляд:

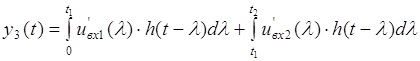
Повна реакція кола на діючий сигнал:

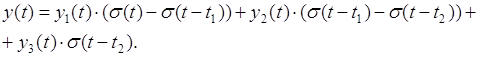 (1.8)

Графік реакції на рис. 1.3, а числові дані в таблиці 1.2.

Таблиця 1.2 Значення реакції кола на трикутний імпульс

0	0
3	38.119
6	67.02
9	32.094
12	-12.196
15	-27.006
18	-19.127
21	-13.721
24	-10.003
27	-7.435
30	-5.654
33	-4.409
36	-3.532
39	-2.906
42	-2.454
45	-2.12

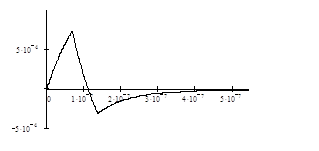
Рисунок 1.3 – Значення реакції кола на трикутний імпульс

Перевіримо отриманий результат графічною інтерпретацією процедури розрахунків методом інтеграла Дюамеля. Використаємо для цього формулу інтеграла Дюамеля через імпульсну характеристику (1.1). Відповідно до формули (1.1) миттєвим значенням  реакції для моментів часу  відповідає площа, яка є алгебраїчною сумою двох площ: перша – це площа фігури, яка обмежується віссю абсцис і графіком функції, отриманої в результаті добутку зсунутого в точку  на осі абсцис дзеркального відображення відносно осі координат неперервної складової (без стрибка) імпульсної характеристики  та діючого сигналу; друга – пропорційна добутку початкового значення  перехідної характеристики на миттєве значення .

Розглянемо момент часу . Графіки вхідного сигналу та відповідно копії  імпульсної характеристики на рис.1.4,а.

Очевидно, що добуток цих функцій дорівнює дорівнює нулю, а отже дорівнює дорівнює нулю і перша площа . Таким чином, початкове значення реакції також дорівнює нулю .

Розглянемо момент часу . Графіки вхідного сигналу та відповідно копії  імпульсної характеристики на рис.1.4,б. Реакція в цей момент часу зростає. Площа  дорівнює .

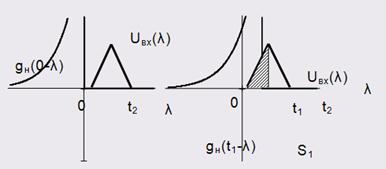
Рисунок 1.4

Розглянемо момент часу . Графіки вхідного сигналу та відповідної копії  імпульсної характеристики (рис.1.5,а). Для даного моменту часу , а отже площа від’ємна [4].

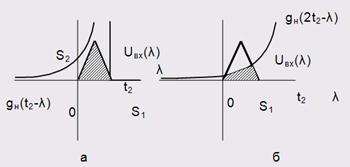
Рисунок 1.5

Розглянемо момент часу . Графіки вхідного сигналу та відповідної копії  імпульсної характеристики (рис.1.5,б). Для даного часу друга площа є від’ємною, але значно меншою ніж у попередніх випадках. Очевидно, що при подальшому зсуві копії імпульсної характеристики, виходячи з її виду, площа  буде зменшуватися, все більше наближаючись до нуля. А отже, знайдена нами реакція обчислена вірно.