Навигация
Зонная теория твёрдых тел является моделью изучения электронных свойств идеальных периодических структур кристаллов. В этом суть первого приближения
1. Зонная теория твёрдых тел является моделью изучения электронных свойств идеальных периодических структур кристаллов. В этом суть первого приближения.
Ранее приведённое уравнение Шредингера удобно представить в виде:
![]()
где
![]() - гамильтониан кристалла;
- гамильтониан кристалла;
![]() - собственная волновая функция гамильтониана;
- собственная волновая функция гамильтониана;
Е – энергия кристалла.
Оператор Гамильтона включает в себя: оператор кинетической энергии электронов - ![]() ; оператор кинетической энергии ядер -
; оператор кинетической энергии ядер - ![]() ; потенциальную энергию попарного взаимодействия электронов
; потенциальную энергию попарного взаимодействия электронов ![]() , ядер
, ядер ![]() , электронов с ядрами -
, электронов с ядрами - ![]() . В этих обозначениях уравнение имеет вид:
. В этих обозначениях уравнение имеет вид:
![]()
2. Второе упрощение называют упрощением Борна-Оппенгеймера, при котором всю систему частиц разделяют на электроны и атомные ядра и рассматривают их кинетические энергии в равновесном состоянии. Пользуясь законом равенства количества движения в системе ядро-электрон без учёта количества движения от внешнего источника можем записать:
![]()
Для водорода M=1840m. Из-за разницы масс будет и разница в скоростях теплового движения ядер и электронов. Ядра можно считать неподвижными по сравнению с электронами. Таким образом, движение электронов и ядер можно считать независимым, проходящим без обмена энергией между электронной и ядерной подсистемами частиц. В этом и состоит смысл адиобатического приближения (А.И. Ансельм “Введение в теорию полупроводников”, Физмат. изд. 1963 – в этой книге можно найти много интересного о методах решения уравнения Шредингера для кристалла).
3. Третье допущение называют одноэлектронным приближением. Рассмотрим его более подробно в следующем параграфе.
Таким образом, в основе зонной теории, приводящей к зонной картине электронного энергетического спектра твёрдого тела, лежат следующие главные приближения:
1. Твёрдое тело представляет собой идеально переодический кристалл.
2. Равновесные положения узлов кристаллической решётки фиксированы, т.е. ядра атомов считаются неподвижными (адиабатическое приближение). Малые колебания атомов вокруг равновесных положений, которые могут быть описаны как фононы, вводятся в последствии как возмущения электронного энергетического спектра.
3. Многоэлектронная задача сводится к одноэлектронной: воздействие на данный электрон всех остальных описывается некоторым усреднённым переодическим полем.
4. Одноэлектронное описание многоэлектронных систем.
5. Идея одноэлектронного приближения ведёт своё начало с доквантово-механической – боровской – теории сложных атомов. Эта модель основана на допущении, что действие на данный электрон всех ядер и всех остальных электронов системы приближённо можно заменить действием некоторого усреднённого “эффективного” поля, потенциальная энергия электрона в котором – так называемый “эффективный одноэлектронный потенциал”
![]() (1)
(1)
зависит только от координат этого электрона (x,y,z). Таким путём исследование различных многоэлектронных систем сводится к исследованию движения одного электрона в полях с различными потенциалами.
В дальнейшем нас будут интересовать не любые состояния электрона в поле (1), а лишь так называемые стационарные состояния. Таким состояниям в боровской модели атома соответствовали устойчивые орбиты электронов. В квантовой механике боровские орбиты для стационарных состояний электрона заменяются определёнными во всём трёхмерном пространстве одноэлектронными волновыми функциями,
![]() (2)
(2)
которые называют также орбиталями.
Стационарным состояниям соответствуют определённые энергетические уровни. Таким образом последовательности одноэлектронных орбиталей для стационарных состояний электрона в поле (1)
![]() … (3)
… (3)
отвечает последовательность одноэлектронных уровней
![]() … (4)
… (4)
или одноэлектронный энергетический спектр системы. Может случиться, что нескольким функциям (3) соответствует один и тот же энергетический уровень. Такой уровень называется вырожденным, а число разных функций, соответствующих этому уровню называют кратностью вырождения уровня.
Ψ1 --> E1 E1 - вырожденный уровень
Ψ2 --> E1 2 кратность вырождения
Вышесказанного вполне достаточно, чтобы понять чем занимаются почти все специалисты по электронной структуре кристаллов. Они вычисляются для разных систем орбитами (3) и уровни (4), поскольку в в одноэлектронном приближении наборы (3) и (4) исчерпывают все, что можно сказать об электронном строении и электронных свойствах любой системы.
Действительно, система из N электронов описывается в одноэлектронной модели просто как совокупность частиц, каждая из которых находится на определенной орбитали (3). При этом стремление к минимальной энергии заставляет электроны занимать возможно более низкие уровни, однако в силу принципа Паули на каждой орбитали должно находиться не более двух электронов (в этом случае они имеют противоположные спины). Тогда оптические свойства системы определяются одноэлектронными переходами из одного состояния ( Ψί) в другое (Ψj), а энергия , необходимая для отрыва электрона с некоторой орбитали Ψj – так называемый «орбитальный потенциал ионизации», - будет равна энергии соответствующего одноэлектронного уровня
Eί, взятый с обратным знаком. В то время как схема уровней (4) дает информацию об оптических свойствах, а также об электропроводности кристаллов, вид орбиталей позволяет судить о распределении электронной плотности в системе.
Это обстоятельство связанно с физическим смыслом волновой функции. Квадрат модуля волновой функции в некоторой точке пространства пропорционален вероятности нахождения электрона в этой точке пространства. Если взять, как это делают обычно, орбитали (3) нормированными т.е. :
|Ψ|2dV=1
где интеграл взят по всему пространству, то величина |Ψ|2 для каждой из орбиталей даст распределение вероятностей для электрона на соответствующей орбитали.
Результирующая электронная плотность для всей системы определяется выражением
ρ(r)= 2Σ'|Ψί|2 +Σ''|Ψj|2
где Σ' – означает суммирование по дважды занятым орбиталям, а Σ'' – суммирование по однократно занятым орбиталям.
Способы решения одноэлектронных задач связанны с именами Хартри и Фока. Особенно много в этом направлении сделал ленинградский ученый Владимир Александрович Фок. Метод Хартри-Фока позволяет много-электронную задачу свести к одноэлектронной, путем замены взаимодействия каждого электрона с усредненным полем всех остальных электронов. Обозначив потенциальную энергию i-го электрона в усредненном поле (Ωί), и зависимую не только от движения всех электронов, но и от движения данного электрона, мы переходим к усредненному полю. Усредненное поле не только определяет движение электрона, но и само зависит от его движения. Его вызывают самосогласованным. С помощью самосогласованного поля удалось значительно продвинуться в решении уравнения Шредингера.
Приближение сильно и слабо связанных электронов
Несмотря на значительное упрощение, которое достигается одноэлектронным приближением, точное решение уравнения Шредингера оказывается очень сложным. Поэтому для его решения были разработаны различные приближения, в частности приближения, в частности приближения сильно и слабо связанных электронов.
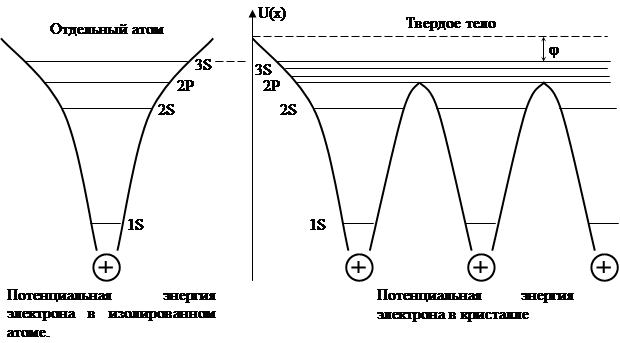
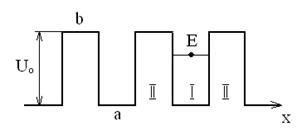
Физический смысл этих приближений заключается в следующем: из рис.1 видно, что в кристалле имеются области, где потенциал решетки меняется очень резко, и области, где он меняется слабо. Первый из них располагается непосредственно вблизи ядер. Электрическое поле в этих областях практически такое же как и в изолированных атомах. Области, где потенциал меняется слабо, располагаются между ядрами. На их долю приходится основная доля объема кристалла.
В соответствии с этим при выборе потенциальной энергии U(r) весь объем кристалла удобно делить на две части:
Похожие работы
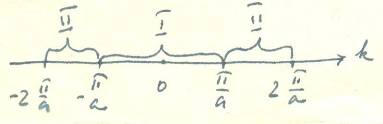
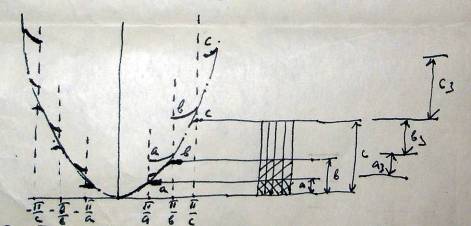
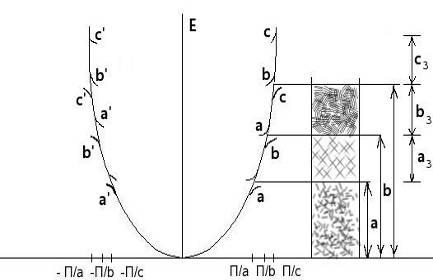
... энергий и претерпевает разрывы на границах зон Бриллюэна. Энергетические зоны являются следствием периодической структуры кристалла и представляют собою фундаментальные характеристики электронной структуры твердого тела. – граница зоны, это вектор обратной решетки. Области значений , при которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв, называются зонами ...
... лежат выше Emax. В промежутке между Emin и Emax не лежит ни одно собственное значение энергии электрона, т.е. область между Emin и Emax представляет собой запрещённую зону энергии. О структуре энергетических зон. В трёхмерном кристалле периодичность решётки в разных направлениях различная: a ≠ b ≠ c. Поэтому в трёхмерном векторном пространстве (kx, ky, kz) kx = ±nπ/a, ky = ...
... «преобразования Лоренца», «группа Лоренца», показал, что невозможно обнаружить абсолютное движение, исходя из представлений об эфире и связанной с ним привеллигированной системы отсчета. Период современной физики (1905 - 1931гг.) 1905г. А.Пуанкаре и А.Эйнштейн установили ковариантность уравнений Максвелла относительно «группы Лоренца». А.Эйнштейн выдвинул гипотезу о квантовом характере ...
... висит от природы тел. виях опыта). гелия. тем же самым,что и 2ой з.Нью- r1(w,T) = r2(w,T) = rn(w,T) 2. Max кинетическая энерг. вы- Физика атома и ядра 2.Корпускулярно волновой дуатона в класич.мех. a(w,T) a2(w,T) =… an(w,T)=битых электронов независит от лизм ...

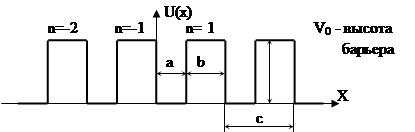

0 комментариев