Навигация
Области со слабым полем, в которых
1. Области со слабым полем, в которых
U(r)=U0(r)+δU(r), δU(r)<<U0(r) (10)
где U0(r)=const представляет собою потенциальную энергию электрона в поле положительных ионов в предположении, что это поле компенсировано полем всех остальных электронов, кроме данного; δU(r) учитывает неполную локальную компенсацию поля ионов электронами. Она имеет периодический характер с периодом, равным
На области с сильным полем в которых:
U(r)=Ua+δU(r) δU(r)<<Ua (11)
где Ua - потенциальная энергия электрона в изолированном атоме.
Она является периодической функцией с периодом равным постоянной решетки; δU(2) поправочный член, учитывающий влияние на эту энергию соседних узлов решетки. Волновые функции электронов, обладающих различной энергией, имеют различный характер локализации в объеме кристалла. Волновые функции внутренних электронов на незначительном расстоянии от ядер обращаются практически в ноль и для них пригодна формула (I I). Это будет приближение сильной связи. Для внешних валентных электронов лучше подходит приближение слабо связанных электронов в котором используется формула (I0).
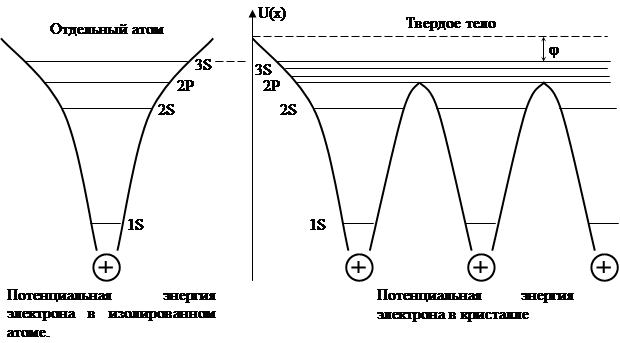
Превращение энергетических уровней свободных атомов в энергетические зоны при образовании кристалла.
Взаимодействие атомов при образовании твердого тела приводит к расширению энергетических уровней атомов и превращению их в кристалле в энергетические зоны.
В атомах время жизни электрона в возбужденном состоянии τ = 10-8c
Вспомним принцип неопределенности для энергии
∆E ∆t ≥ ħ
∆t ≈ τ
тогда
∆E ≈ ħ / τ ≈ 10-7 эВ (ħ = 10-15 эВс)
Такова естественная ширина спектральных линий, испускаемых атомами.
В кристалле все электроны благодаря туннельному эффекту имеют возможность переходить от атома к атому. В результате уменьшается степень локализации электронов на определенных атомах, что изменяет значение неопределенностей их энергий, т.е. приводит к размытию уровней энергии и превращению их а полосы или зоны.
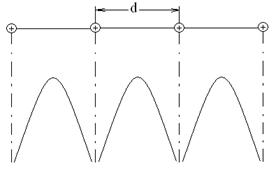
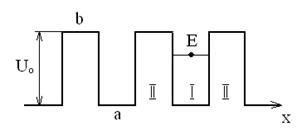
Так как глубина потенциального поля не играет принципиальной роли, можно заменить потенциальный рельеф кристалла рельефом с конечной глубиной. Кроме этого непрямоугольные барьеры в модели кристалла удобно заменить прямоугольными. Такую модель потенциального рельефа называют моделью Кронинга-Пенни.
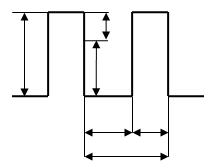
Мы уже знаем как определяется прозрачность такого барьера:
D = D0 e-4π/h![]()
![]()
Если ширина потенциальной ямы равна α, а скорость движения электрона равна υ, то за 1 секунду электрон подойдет к барьеру υ/α раз.
ν = υ/α D - дает частоту перехода электрона в соседний атом
ν = υ/α D0 e-4π/h![]()
![]()
Величина τ обратная ν выражает среднее время пребывания электрона у определенного атома
τ = 1/ ν ≈ 1/ υ/α D0 e-4π/h![]()
![]()
так как α ≈ 10-8 см; υ ≈ 108 см/с; D0 ≈ 1; υ/α ≈ 1016с-1
Для изолированных атомов d ≥ 30Å (среднее расстояние между молекулами газа при нормальных условиях). U-E – энергия ионизации атома. Для Na
U-E = 10 эВ. Найдем τ в этом случае:
τ ≈ 1020лет; ν ≈ 10-27с-1
В кристалле b ≈ 1Å, тогда ν ≈ 1015с-1 ; τ ≈ 10-20 с
При такой частоте перехода валентных электронов от атома к атому теряет, очевидно, смысл говорить о принадлежности их определенным атомам.
Таким образом туннельный эффект в кристалле доводит среднее время жизни валентного электрона в определенном узле решетки до τ ≈ 10-15с. В соответствии с принципом неопределенности, неопределенность в значении энергии таких электронов равна:
∆E ≈ 10-12эрг ≈ 1эВ
Это означает, что энергетический уровень валентных электронов, имеющий в изолированном атоме ширину 10-7эВ превращается в кристалле в энергетическую зону шириной порядка единиц электроновольт.
Для электронов внутренних оболочек натрия картина изменяется. Например, для электронов 1s (U-E ≈ 1000 эВ, d ≈ 3Å в результате ν ≈ 10-27 с-1; τ ≈ 1020лет) энергетические уровни этих атомов в кристалле такие же узкие, как и в отдельном атоме. По мере перехода к валентным электронам высота и ширина потенциального барьера уменьшается, вероятность туннельного перехода электронов увеличивается, вследствие чего растет ширина энергетических зон.
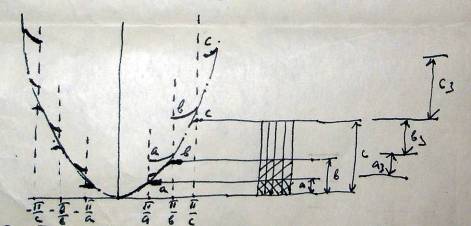
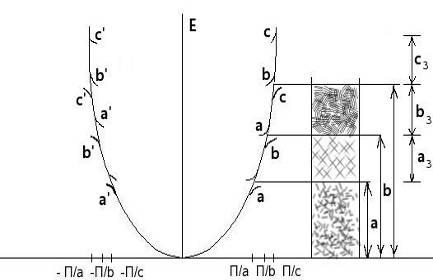
На рисунке снизу приведены урони изолированного атома натрия, слева – образование
Зон, обусловленное расширением уровней при уменьшении расстояния между атомами. Электрические свойства твердых тел в основном определяют особенностями образования энергетических зон при сближении атомов и образовании кристалла.
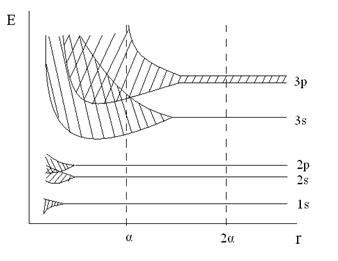
Рис. Расширение энергетических уровней при сближении атомов Na.
ЛИТЕРАТУРА
1. Мирошников М.М. Теоретические основы оптико-электронных приборов: учебное пособие для приборостроительных вузов. -- 2-е издание, перераб. и доп.—Спб.: Машиностроение,2003 -- 696 с.
2. Порфирьев Л.Ф. Теория оптико-электронных приборов и систем: учебное пособие.— Спб.: Машиностроение,2003 -- 272 с.
3. Кноль М., Эйхмейер И. Техническая электроника, т. 1. Физические основы электроники. Вакуумная техника.—М.: Энергия, 2001.
Похожие работы
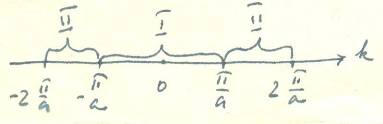
... энергий и претерпевает разрывы на границах зон Бриллюэна. Энергетические зоны являются следствием периодической структуры кристалла и представляют собою фундаментальные характеристики электронной структуры твердого тела. – граница зоны, это вектор обратной решетки. Области значений , при которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв, называются зонами ...
... лежат выше Emax. В промежутке между Emin и Emax не лежит ни одно собственное значение энергии электрона, т.е. область между Emin и Emax представляет собой запрещённую зону энергии. О структуре энергетических зон. В трёхмерном кристалле периодичность решётки в разных направлениях различная: a ≠ b ≠ c. Поэтому в трёхмерном векторном пространстве (kx, ky, kz) kx = ±nπ/a, ky = ...
... «преобразования Лоренца», «группа Лоренца», показал, что невозможно обнаружить абсолютное движение, исходя из представлений об эфире и связанной с ним привеллигированной системы отсчета. Период современной физики (1905 - 1931гг.) 1905г. А.Пуанкаре и А.Эйнштейн установили ковариантность уравнений Максвелла относительно «группы Лоренца». А.Эйнштейн выдвинул гипотезу о квантовом характере ...
... висит от природы тел. виях опыта). гелия. тем же самым,что и 2ой з.Нью- r1(w,T) = r2(w,T) = rn(w,T) 2. Max кинетическая энерг. вы- Физика атома и ядра 2.Корпускулярно волновой дуатона в класич.мех. a(w,T) a2(w,T) =… an(w,T)=битых электронов независит от лизм ...

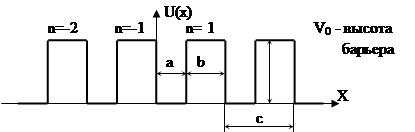

0 комментариев