Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу

9.     Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу.

10.           Для представления в полярных координатах, верно следующее

a.                             Площадь полярного сектора , при :

b. В частности, площадь каждой петли .

c.  Радиус кривизны лемнискаты есть

Построение лемнискаты

·        с помощью трёх отрезков

Это один из наиболее простых и быстрых способов, однако требует наличия дополнительных приспособлений.

На плоскости выбираются две точки – A и B – будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба – C и D). При этом необходимо соблюсти пропорции отрезков: AC=BD=, CD=AB. Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.

·        при помощи секущих (способ Маклорена)

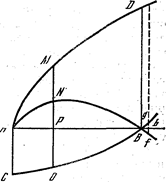
Строится окружность радиуса с центром в одном из фокусов. Из середины O фокусного отрезка строится произвольная секущая OPS (P и S – точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки OM₁ и OM₂, равные хорде PS. Точки M₁, M₂ лежат на разных петлях лемнискаты.

 

Неравенство Бернулли

Неравенство Бернулли (названо в честь Иоганна) утверждает: если, то

 

Доказательство проводится методом математической индукции по n. При n = 0 неравенство, очевидно, верно. Допустим, что оно верно для n, докажем его верность для n+1:

, ч.т.д.

  Примечания:

·         Неравенство справедливо также для вещественных  (при)

·         Неравенство также справедливо для  (при), но указанное выше доказательство по индукции в случае не работает.

Распределение Бернулли

Распределение Бернулли (названо в честь Якоба) моделирует случайный эксперимент произвольной природы, когда заранее известна вероятность успеха или неудачи.

Случайная величина X имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями p и соответственно. Таким образом:

 

P (X = 1) = p

P (X = 0) = q

Принято говорить, что событие {X = 1} соответствует «успеху», а {X = 0} «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.

 

E[X] = p,

D[X] = pq.

Вообще, легко видеть, что

 

E[] = p .

 

Числа и многочлены Бернулли

Числа Бернулли – последовательность рациональных чисел B₀, B₁, B₂,… найденная Якобом Бернулли в связи с вычислением суммы одинаковых степеней натуральных чисел:

Для чисел Бернулли существует следующая реккурентная формула:

Первые четырнадцать чисел Бернулли равны:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
	1			0		0		0		0		0		0

Свойства

·         Все числа Бернулли с нечетными номерами, кроме B₁, равны нулю, знаки B_2n чередуются.

·         Числа Бернулли являются значениями при x = 0 многочленов Бернулли 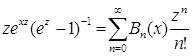,и равны: B_n = B_n(0).

Коэффициентами разложения некоторых элементарных функций в степенные ряды часто служат числа Бернулли. Например:

·         Экспоненциальная производящая функция для чисел Бернулли:

·          

,

·        

·        

·         Эйлер указал на связь между числами Бернулли и значениями дзета-функции Римана ζ(s) при четных s = 2m:

Из чего следует

B_n = − nζ (1 − n) для всех n.

·        

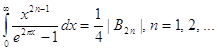
Список литературы

1. Белл Э.Т. Творцы математики. М.: Просвещение, 1979.

2. Боголюбов А.Н. Математики. Механики. Биографический справочник. Киев: Наукова думка, 1983.

3. История математики. Под редакцией Юшкевича А.П. в трёх томах. Том 3 Математика XVIII столетия. М.: Наука, 1972.