IX математический симпозиум.
Закономерность распределения простых чисел в ряду натуральных чисел.
г. Волжский.
05-11 октября 2008 года.
Белотелов В.А.
Нижегородская обл.
г. Заволжье
vbelotelov@mail. ru
Простые числа? – Это просто!?
Узнав о важной роли простых чисел (ПЧ) в криптографии, генерации случайных чисел, навигации, имитационном моделировании и о том, что нужна закономерность распределения ПЧ в ряду натуральных чисел, не являясь математиком, всё же рискнул заняться решением этой задачи. Результат ниже.
Для начала выписал ряд ПЧ. Конечно же, это было сделано с целью заметить, хоть какую бы, закономерность. С этой же целью были вычислены разности между соседними числами ряда ПЧ. Было замечено, что иногда появлялась последовательность разностей 6-4-2-4-2-4-6-2. Там, где эта последовательность нарушалась, были введены составныё числа (СЧ). Результат представлен в таблице 1, СЧ в которой подчёркнуты. Числа 2, 3, 5, являясь ПЧ, из рассмотрения всё же были убраны. Это первое исключение из правил. Вторая вольность заключалась введением в рассмотрение числа 1, зная, что единица не является простым числом.
Целью же было найти закономерность среди ПЧ + СЧ, а потом уже найти закономерность среди ПЧ. Стратегия поиска закономерности ПЧ заключалась в следующей логической формуле:
(закономерность ПЧ+СЧ) – (закономерность СЧ) = закономерность ПЧ.
Из ПЧ + СЧ, представленных в таблице 1, была составлена система из восьми арифметических прогрессий. Результат представлен в таблице 2.
Разности всех восьми прогрессий равны 30 и их первые члены равны соответственно 1, 7, 11, 13, 17, 19, 23, 29, а сами ряды обозначены через R1, R7,R11, R13, R17, R19, R23, R29. СЧ, как и в таблице 1, подчёркнуты и сверху расписаны в виде произведений двух чисел. Можно сформулировать правило, по которому в любой из восьми арифметических прогрессий распределены СЧ.
Если в арифметической прогрессии, какой – либо член an можно представить в виде двух сомножителей fxp, то последующие члены этой прогрессии an+mf являются произведением fx(p+md), а члены an+kp произведением px(f+kd), где m и k любые натуральные
числа, а d – разность этой прогрессии.
Данное правило не нуждается в доказательстве, т. к. фактически следует из определения арифметической прогрессии. Но для обеспечения закономерности ПЧ имеет большое значение. Во - первых, оно запрещает поиск рядов ПЧ, подчиняющихся одной арифметической прогрессии, т. к. любое простое число an можно представить в виде anх1, и тогда в любом ряде через число членов an, появляется составное число anх(1+d).
Во – вторых, в любой арифметической прогрессии появление дополнительных составных чисел возможно только в сочетании с разностью именно этой прогрессии.
Это правило можно сформулировать для любого числа сомножителей, но в данном случае интерес представляет число сомножителей равное двум.
В качестве примера рассмотрим в ряде R1 четвёртый член равный 91=7х13. Ближайшим членом в ряде R1 кратным семи является число 301, отстоящее от числа 91 на семь номеров, соответственно, число 301 принадлежит ряду СЧ. Число 301 является произведением 7х43 (301=7х43), и с номера этого числа равного 11, каждое сорок третье число, тоже делится на 43 и, соответственно, принадлежит к ряду СЧ. Дальше это можно не описывать, т. к. это хорошо видно в таблице 2.
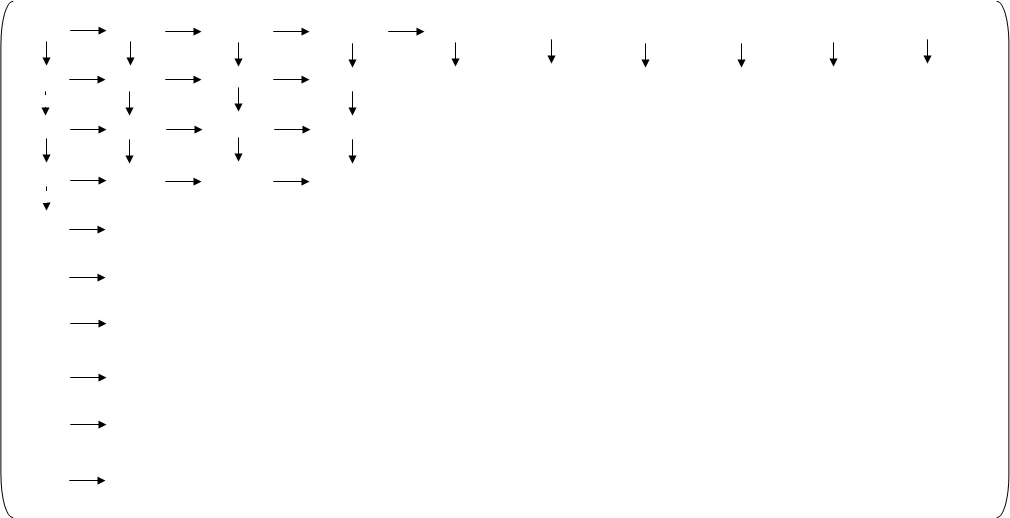
Расписав таблицу 2 в виде математических символов, удалось получить систему из восьми формул, расписанных в виде разности сумм, см. таблицу 3. Во всех восьми формулах системы, члены с рядами двойных сумм служат фильтрами, удаляющими СЧ из ряда ПЧ+СЧ, и задают работу фильтров в виде матриц.
В таблице 4 изображено распределение номеров СЧ в ряде R1, определяемых вторым членом формулы. Это матрица, в которой и по столбцам и по строкам арифметические прогрессии.
В формулах индексы ![]() и
и ![]() обозначают столбцы и строки подобных матриц, сами же
обозначают столбцы и строки подобных матриц, сами же ![]() и
и ![]() дополнительными индексами не отягощаю. Без
дополнительными индексами не отягощаю. Без ![]() и
и ![]() описать работу матриц не смог, а формальная фраза, что в выражении
описать работу матриц не смог, а формальная фраза, что в выражении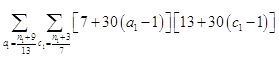 под суммой произведений подразумеваются всевозможные их комбинации в зависимости от значений a1 и с1, будет неверна. Ибо все члены с номерами при
под суммой произведений подразумеваются всевозможные их комбинации в зависимости от значений a1 и с1, будет неверна. Ибо все члены с номерами при ![]() >1 и
>1 и ![]() >1 из формулы выпадают.
>1 из формулы выпадают.
Система формул арифметических прогрессий, позволяющая вычислять ПЧ, получилась достаточно громоздкой, но закономерность обозначена.
Данная статья была подготовлена для публикации в научном журнале с математическим уклоном. Пока шёл поиск данного журнала, путём несложных умозаключений, была составлена система рядов арифметических прогрессий с разностью 10. Результат в таблице 5 и 6. Всё было расписано по образцу и подобию предыдущего материала. В таблице 7 изображена матрица для номеров второго члена формулы 1 таблицы 6.
Не начав переписывать статью заново, в связи с открытием новой системы уравнений, опять же путём размышлений, были расписаны арифметические прогрессии с разностью 2 и 1, т.е. при разности единица ПЧ были напрямую увязаны с натуральным рядом. Результат в таблице 8 и 9.
Всё расписано, как и в случаях с системами уравнений арифметических прогрессий разностей 30 и 10. И после этого наступил момент истины.
Оказалось, что подобных уравнений можно составить бесконечное множество. Навскидку – это арифметические прогрессии с разностью 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60, и т.д. Даже в перечисленном до разности 60 указаны не все.
Обобщающий вывод:
ПЧ можно представить комбинацией арифметических прогрессий. Таких комбинаций бесконечное множество. Но каждая из комбинаций систем арифметических прогрессий позволяет только единственное представление ПЧ при заданной разности прогрессий задающий ряды ПЧ+СЧ.
| 1 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 49 |
| 53 | 59 | |||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 61 | 67 | 71 | 73 | 77 | 79 | 83 | 89 | 91 | 97 | 101 | 103 | 107 | 109 | 113 | 119 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 121 | 127 | 131 | 133 | 137 | 139 | 143 | 149 | 151 | 157 | 161 | 163 | 167 | 169 | 173 | 179 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 181 | 187 | 191 | 193 | 197 | 199 | 203 | 209 | 211 | 217 | 221 | 223 | 227 | 229 | 233 | 239 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 241 | 247 | 251 | 253 | 257 | 259 | 263 | 269 | 271 | 277 | 281 | 283 | 287 | 289 | 293 | 299 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 301 | 307 | 311 | 313 | 317 | 319 | 323 | 329 | 331 | 337 | 341 | 343 |
| 347 | 349 | 353 | 359 | |||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 361 | 367 | 371 | 373 | 377 | 379 | 383 | 389 | 391 | 397 | 401 | 403 | 407 | 409 | 413 | 419 |
| |||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 421 | 427 | 431 | 433 | 437 | 439 |
| 443 | 449 | 451 | 457 | 461 | 463 | 467 | 469 | 473 | 479 | |||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 481 | 487 | 491 | 493 | 497 | 499 | 503 | 509 | 511 | 517 | 521 | 523 | 527 | 529 | 533 | 539 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 541 | 547 | 551 | 553 | 557 | 559 | 563 | 569 | 571 | 577 | 581 | 583 | 587 | 589 | 593 | 599 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 601 | 607 | 611 | 613 | 617 | 619 | 623 | 629 | 631 | 637 |
| 641 | 643 |
| 647 | 649 | 653 | 659 | ||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 661 | 667 | 671 | 673 | 677 | 679 | 683 | 689 | 691 | 697 | 701 | 703 | 707 | 709 | 713 | 719 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | ||||||||||||||||
| 721 | 727 | 731 | 733 | 737 | 739 | 743 | 749 | 751 | 757 | 761 | 763 | 767 | 769 | 773 | 779 | ||||||||||||||||
| 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 | 6 | 4 | 2 | 4 | 2 | 4 | 6 | 2 |
![]()
|
| 7х13 | 11х11 | 7х43 | 19х19 | 17х23 | 11х41 | 13х37 | 7х73 | |||||||||||
| 1 | 31 | 61 | 91 | 121 | 151 | 181 | 211 | 241 | 271 | 301 | 331 | 361 | 391 | 421 | 451 | 481 | 511 | 541 | 571 |
| 11х17 | 7х31 | 13х19 | 7х61 | 11х47 | |||||||||||||||
| 7 | 37 | 67 | 97 | 127 | 157 | 187 | 217 | 247 | 277 | 307 | 337 | 367 | 397 | 427 | 457 | 487 | 517 | 547 | 577 |
| 7х23 | 13х17 | 11х31 | 7х53 | 19х29 | 7х83 | ||||||||||||||
| 11 | 41 | 71 | 101 | 131 | 161 | 191 | 221 | 251 | 281 | 311 | 341 | 371 | 401 | 431 | 461 | 491 | 521 | 551 | 581 |
| 7х19 | 11х23 | 7х49 | 13х31 | 17х29 | 7х79 | 11х53 | |||||||||||||
| 13 | 43 | 73 | 103 | 133 | 163 | 193 | 223 | 253 | 283 | 313 | 343 | 373 | 403 | 433 | 463 | 493 | 523 | 553 | 583 |
| 7х11 | 7х41 | 13х29 | 11х37 | 19х23 | 7х71 | 17х31 | |||||||||||||
| 17 | 47 | 77 | 107 | 137 | 167 | 197 | 227 | 257 | 287 | 317 | 347 | 377 | 407 | 437 | 467 | 497 | 527 | 557 | 587 |
| 7х7 | 13х13 | 7х37 | 17х17 | 11х29 | 7х67 | 23х23 | 13х43 | 19х31 | |||||||||||
| 19 | 49 | 79 | 109 | 139 | 169 | 199 | 229 | 259 | 289 | 319 | 349 | 379 | 409 | 439 | 469 | 499 | 529 | 559 | 589 |
| 11х13 | 7х29 | 17х19 | 7х59 | 11х43 | 13х41 | ||||||||||||||
| 23 | 53 | 83 | 113 | 143 | 173 | 203 | 233 | 263 | 293 | 323 | 353 | 383 | 413 | 443 | 473 | 503 | 533 | 563 | 593 |
| 7х17 | 11х19 | 13х23 | 7х47 | 11х49 7х77 | |||||||||||||||
| 29 | 59 | 89 | 119 | 149 | 179 | 209 | 239 | 269 | 299 | 329 | 359 | 389 | 419 | 449 | 479 | 509 | 539 | 569 | 599 |
![]()
|
| 7х103 | 11х71 | 29х29 | 13х67 | 17х53 | 19х49 7х133 | 31х31 | 23х47 | 11х101 | 7х163 | |||||||||
| 601 | 631 | 661 | 691 | 721 | 751 | 781 | 811 | 841 | 871 | 901 | 931 | 961 | 991 | 1021 | 1051 | 1081 | 1111 | 1141 | 1171 |
| 13х49 7х91 | 23х29 | 17х41 | 19х43 | 11х77 7х121 | 13х79 | 7х151 | 31х37 | 11х107 | |||||||||||
| 607 | 637 | 667 | 697 | 727 | 757 | 787 | 817 | 847 | 877 | 907 | 937 | 967 | 997 | 1027 | 1057 | 1087 | 1117 | 1147 | 1177 |
| 13х47 | 11х61 | 17х43 | 7х113 | 23х37 | 13х77 11х91 7х143 | 19х59 | |||||||||||||
| 611 | 641 | 671 | 701 | 731 | 761 | 791 | 821 | 851 | 881 | 911 | 941 | 971 | 1001 | 1031 | 1061 | 1091 | 1121 | 1151 | 1181 |
| 19х37 | 7х109 | 13х61 | 11х83 | 23х41 | 7х139 | 17х59 | 13х91 7х169 | ||||||||||||
| 613 | 643 | 673 | 703 | 733 | 763 | 793 | 823 | 853 | 883 | 913 | 943 | 973 | 1003 | 1033 | 1063 | 1093 | 1123 | 1153 | 1183 |
| 7х101 | 11х67 | 13х59 | 7х131 | 19х53 | 17х61 | 11х97 | 23х49 7х161 | 13х89 | |||||||||||
| 617 | 647 | 677 | 707 | 737 | 767 | 797 | 827 | 857 | 887 | 917 | 947 | 977 | 1007 | 1037 | 1067 | 1097 | 1127 | 1157 | 1187 |
| 11х59 | 7х97 |
| 17х47 | 7х127 | 13х73 | 11х89 |
| 7х157 |
| 19х61 | 29х41 | ||||||||
| 619 | 649 | 679 | 709 | 739 | 769 | 799 | 829 | 859 | 889 | 919 | 949 | 979 | 1009 | 1039 | 1069 | 1099 | 1129 | 1159 | 1189 |
| 7х89 | 23х31 | 11х73 | 17х49 7х119 | 19х47 | 13х71 | 7х149 | 29х37 | 11х103 | |||||||||||
| 623 | 653 | 683 | 713 | 743 | 773 | 803 | 833 | 863 | 893 | 923 | 953 | 983 | 1013 | 1043 | 1073 | 1103 | 1133 | 1163 | 1193 |
| 17х37 | 13х53 | 7х107 | 19х41 | 11х79 | 29х31 | 7х137 | 23х43 | 13х83 | 17х67 | 7х167 | 11х109 | ||||||||
| 629 | 659 | 689 | 719 | 749 | 779 | 809 | 839 | 869 | 899 | 929 | 959 | 989 | 1019 | 1049 | 1079 | 1109 | 1139 | 1169 | 1199 |
![]()
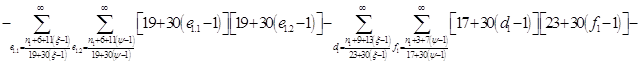
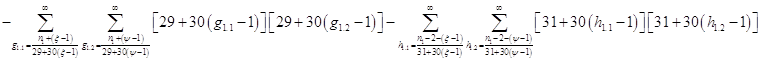
![]()
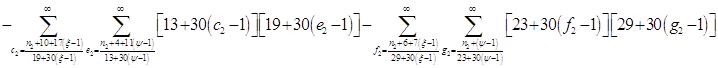
![]()
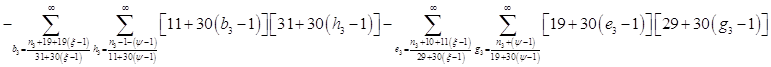
![]()
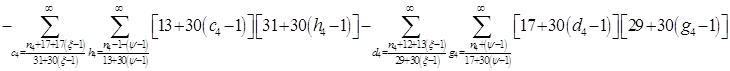
![]()
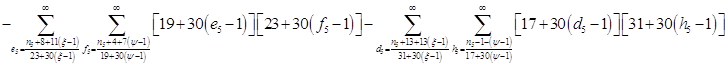
![]()
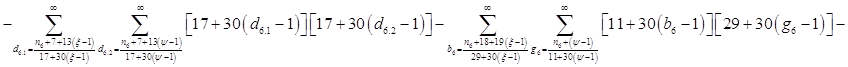
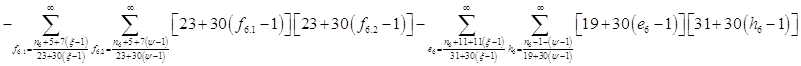
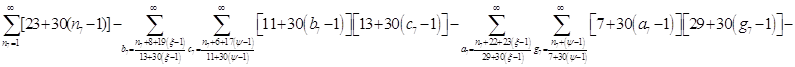
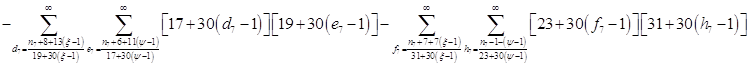
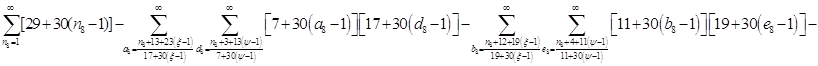
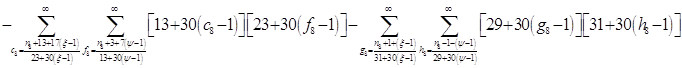
| 4 | +7 | 11 | +7 | 18 | +7 | 25 | +7 | 32 | 39 | 46 | 53 | 60 | 67 | … | |||||
| +13 | +43 | +73 | +103 | +133 | +163 | +193 | +223 | +253 | +283 | ||||||||||
| 17 | +37 | 54 | +37 | 91 | +37 | 128 | 165 | 202 | 239 | 276 | 313 | 350 | … | ||||||
| +43 | +73 | +103 | |||||||||||||||||
| 30 | +67 | 97 | +67 | 164 | +67 | 231 | 298 | 365 | 432 | 499 | 566 | 633 | … | ||||||
| +13 | +43 | +73 | +103 | ||||||||||||||||
| 43 | +97 | 140 | +97 | 237 | +97 | 334 | 431 | 528 | 625 | 722 | 819 | 916 | … | ||||||
| 56 | +127 | 183 | 310 | 437 | 564 | 691 | 818 | 945 | 1072 | 1199 | … | ||||||||
| 69 | +157 | 226 | 383 | 540 | 697 | 854 | 1011 | 1168 | 1325 | 1482 | … | ||||||||
| 82 | +187 | 269 | 456 | 643 | 830 | 1017 | 1204 | 1391 | 1578 | 1765 | … | ||||||||
| 95 | +217 | 312 | 529 | 746 | 963 | 1180 | 1397 | 1614 | 1831 | 2048 | … | ||||||||
| 108 | +247 | 355 | 602 | 849 | 1096 | 1343 | 1590 | 1837 | 2084 | 2331 | … | ||||||||
| 121 | +277 | 398 | 675 | 952 | 1229 | 1506 | 1783 | 2060 | 2337 | 2614 | … | ||||||||
| … | … | … | … | … | … | … | … | … | … |
|
| 3х7 | 3х17 | 9х9 3х27 | 7х13 | 3х37 | 11х11 | 3х47 | 7х23 | 9х19 3х57 | 3х67 | ||||||||||
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 | 101 | 111 | 121 | 131 | 141 | 151 | 161 | 171 | 181 | 191 | 201 |
| 3х11 | 7х9 3х21 | 3х31 | 3х41 | 7х19 | 11х13 | 9х17 3х51 | 3х61 | 7х29 | ||||||||||||
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 | 103 | 113 | 123 | 133 | 143 | 153 | 163 | 173 | 183 | 193 | 203 |
| 3х9 | 3х19 | 7х11 | 3х29 | 9х13 3х39 | 7х21 3х49 | 3х59 | 11х17 | 9х23 3х69 | ||||||||||||
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 | 107 | 117 | 127 | 137 | 147 | 157 | 167 | 177 | 187 | 197 | 207 |
| 3х3 | 3х13 | 7х7 | 3х23 | 9х11 3х33 | 7х17 | 3х43 | 3х53 | 13х13 | 9х21 7х27 3х63 | 11х19 | ||||||||||
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 | 109 | 119 | 129 | 139 | 149 | 159 | 169 | 179 | 189 | 199 | 209 |
|
| 13х17 | 11х21 7х33 3х77 | 9х29 3х87 | 3х97 | 7х43 | 3х107 | 11х31 | 9х39 13х27 3х117 | 19х19 | 7х53 | 3х127 | 17х23 | ||||||||
| 211 | 221 | 231 | 241 | 251 | 261 | 271 | 281 | 291 | 301 | 311 | 321 | 331 | 341 | 351 | 361 | 371 | 381 | 391 | ||
3х71 | 9х27 3х81 | 11х23 | 7х39 3х91 | 3х101 | 17х19 | 9х37 3х111 | 7х49 | 11х33 3х121 | 3х131 | |||||||||||
| 213 | 223 | 233 | 243 | 253 | 263 | 273 | 283 | 293 | 303 | 313 | 323 | 333 | 343 | 353 | 363 | 373 | 383 | 393 | ||
| 9х27 11х27
7х31 | 3х79 | 13х19 | 3х89 | 7х41 | 11х27 9х33 3х99 | 3х109 | 17х21 7х51 3х119 | 13х29 | 9х43 3х129 | |||||||||||
| 217 | 227 | 237 | 247 | 257 | 267 | 277 | 287 | 297 | 307 | 317 | 327 | 337 | 347 | 357 | 367 | 377 | 387 | 397 | ||
| 9х27
| 3х83 | 7х37 | 9х31 3х93 | 17х17 | 13х23 | 3х103 | 11х29 | 7х47 | 19х21 3х113 | 9х41 3х123 | 7х57 3х133 | |||||||||
| 219 | 229 | 239 | 249 | 259 | 269 | 279 | 289 | 299 | 309 | 319 | 329 | 339 | 349 | 359 | 369 | 379 | 389 | 399 |
|
| 3х137 | 9х49 21х21 7х63 3х147 | 11х41 | 3х157 | 13х37 | 3х167 | 7х73 | 9х59 3х177 | 19х29 | 11х51 17х33 3х187 | 7х83 | |||||||||
| 401 | 411 | 421 | 431 | 441 | 451 | 461 | 471 | 481 | 491 | 501 | 511 | 521 | 531 | 541 | 551 | 561 | 571 | 581 | ||
| 7х59 | 9х47 3х141 | 3х151 | 11х43 | 7х69 21х23 3х161 | 17х29 | 19х27 9х57 3х171 | 3х181 | 7х79 | 3х191 | 11х53 | |||||||||
| 403 | 413 | 423 | 433 | 443 | 453 | 463 | 473 | 483 | 493 | 503 | 513 | 523 | 533 | 543 | 553 | 563 | 573 | 583 | ||
| 7х81 9х63
| 3х139 | 7х61 | 19х23 | 3х149 | 9х53 3х159 | 7х71 | 3х169 | 11х47 | 17х31 | 3х179 | 7х81 9х63 3х189 | |||||||||
| 407 | 417 | 427 | 437 | 447 | 457 | 467 | 477 | 487 | 497 | 507 | 517 | 527 | 537 | 547 | 557 | 567 | 577 | 587 | ||
| 11х39 3х143 | 9х51 17х27 3х153 | 7х67 | 3х163 | 3х173 | 23х23 | 11х49 7х77 | 9х61 3х183 | 3х193 | 19х31 | ||||||||||
| 409 | 419 | 429 | 439 | 449 | 459 | 469 | 479 | 489 | 499 | 509 | 519 | 529 | 539 | 549 | 559 | 569 | 579 | 589 |
![]()
![]()
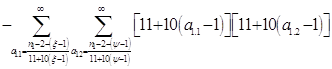
![]()
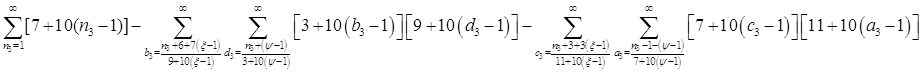
![]()
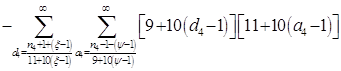
|
|
| 6 |
| 9 |
| 12 |
| 15 | 18 | 21 | 24 | 27 | 30 | … | |||||||
|
+7 |
+17 |
+27 |
|
+47 |
+57 |
|
+77 |
+87 |
| ||||||||||||
| 10 |
| 23 |
| 36 |
| 49 | 62 | 75 | 88 | 101 | 114 | 127 | … | ||||||||
|
|
+17 |
+27 |
+37 |
+47 | |||||||||||||||||
| 17 | +23 | 40 | +23 | 63 | +23 | 86 | 109 | 132 | 155 | 178 | 201 | 224 | … | ||||||||
|
+7 |
|
+17 |
|
+27 |
|
+37 |
+47 | ||||||||||||||
| 24 |
| 57 |
| 90 |
| 123 | 156 | 189 | 222 | 255 | 288 | 321 | … | ||||||||
|
| |||||||||||||||||||||
| 31 |
| 74 | 117 | 160 | 203 | 246 | 289 | 332 | 375 | 418 | … | ||||||||||
| 38 |
| 91 | 144 | 197 | 250 | 303 | 356 | 409 | 462 | 515 | … | ||||||||||
| 45 | +63 | 108 | 171 | 234 | 297 | 360 | 423 | 486 | 549 | 612 | … | ||||||||||
|
| |||||||||||||||||||||
| 52 | +73 | 125 | 198 | 271 | 344 | 417 | 490 | 563 | 636 | 709 | … | ||||||||||
|
| |||||||||||||||||||||
| 59 |
| 142 | 225 | 308 | 391 | 474 | 557 | 640 | 723 | 806 | … | ||||||||||
| 66 |
| 159 | 252 | 345 | 438 | 531 | 624 | 717 | 810 | 903 | … | ||||||||||
| … | … | … | … | … | … | … | … | … | … |
3х3
|
![]()
| 5 |
| 8 |
| 11 |
| 14 |
| 17 |
| 20 |
| 23 |
| 26 |
| 29 | … | ||||||
|
+3 |
+5 |
+7 |
+9 |
+11 |
+13 |
+15 |
+17 |
+19 | |||||||||||||||
| 8 |
| 13 | 18 | 23 | 28 | 33 | 38 | 43 | 48 | … | |||||||||||||
| |||||||||||||||||||||||
| 11 | +7
| 18 | 25 | 32 | 39 | 46 | 53 | 60 | 67 | … | |||||||||||||
|
| |||||||||||||||||||||||
| 14 |
| 23 | 32 | 41 | 50 | 59 | 68 | 77 | 86 | … | |||||||||||||
| |||||||||||||||||||||||
| +11 | 28 | 39 | 50 | 61 | 72 | 83 | 94 | 105 | … | |||||||||||||
|
|
| ||||||||||||||||||||||
| 20 |
| 33 | 46 | 59 | 72 | 85 | 98 | 111 | 124 | … | |||||||||||||
|
| |||||||||||||||||||||||
| 23 |
| 38 | 53 | 68 | 83 | 98 | 113 | 128 | 143 | … | |||||||||||||
|
+3 | |||||||||||||||||||||||
| 26 |
| 43 | 60 | 77 | 94 | 111 | 128 | 145 | 162 | … | |||||||||||||
|
+3 | |||||||||||||||||||||||
| 29 |
| 48 | 67 | 86 | 105 | 124 | 143 | 162 | 181 | … | |||||||||||||
| … | … | … | … | … | … | … | … | … |
2х2
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32,
33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44 ,45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56. 57, 58, 59, 60, 61 …
| ||||
| 4 |
| 6 |
| 8 |
| 10 |
| 12 |
| 14 |
| 16 |
| 18 | … | ||||||||
|
+2 |
+3 |
+4 |
+5 |
+6 |
+7 |
+8 |
+9 | ||||||||||||||||
| 6 |
| 9 |
| 12 |
| 15 |
| 18 |
| 21 |
| 24 |
| 27 | … | ||||||||
|
| ||||||||||||||||||||||
| 8 | +4
| 12 | 16 | 20 | 24 | 28 | 32 | 36 | … | ||||||||||||||
|
| |||||||||||||||||||||||
|
| 15 | 20 | 25 | 30 | 35 | 40 | 45 | … | ||||||||||||||
| |||||||||||||||||||||||
| 12 | +6 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | … | ||||||||||||||
|
|
| ||||||||||||||||||||||
| 14 |
| 21 | 28 | 35 | 42 | 49 | 56 | 63 | … | ||||||||||||||
|
| |||||||||||||||||||||||
| 16 |
| 24 | 32 | 40 | 48 | 56 | 64 | 72 | … | ||||||||||||||
|
| |||||||||||||||||||||||
| 18 |
| 27 | 36 | 45 | 54 | 63 | 72 | 81 | … | ||||||||||||||
| … | … | … | … | … | … | … | … |
5х5 7х7 5х11 5х17 7х13 5х23 11х11 7х19 5х29
![]() 1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121, 127, 133, 139, 145,
1, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61, 67, 73, 79, 85, 91, 97, 103, 109, 115, 121, 127, 133, 139, 145,
5х7 5х13 7х11 5х19 7х17 5х25
5, 11, 17, 23, 29, 35, 41, 47, 53, 59, 65, 71 , 77, 83, 89, 95, 101, 107, 113, 119, 125, 131, 137, 143. 149 …
| 5 |
| 10 |
| 15 |
| 20 |
| 25 |
|
|
+5 |
+11 |
+17 |
+23 |
+29 | |||||
| 10 |
| 21 |
| 32 |
| 43 |
| 54 | … |
|
|
+11 | ||||||||
| 15 | +17
| 32 | 49 | 66 | 83 | … | |||
|
|
+11 | ||||||||
| 20 |
| 43 | 66 | 89 | 112 | … | |||
|
+5 |
| ||||||||
| 25 |
| 54 | 83 | 112 | 141 | … | |||
| … | … | … | … | … |
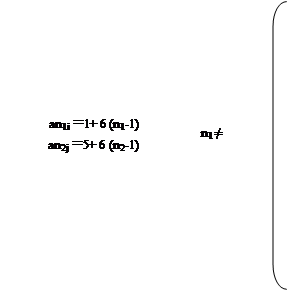
Закономерность распределения простых чисел (дополнение).
Белотелов В.А.
Нижегородская обл.
г. Заволжье
vbelotelov@mail. ru
Там где даны в качестве примера разности арифметических прогрессий и указан их ряд 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60. На самом деле пропусков в ряду быть не должно. Ряд разностей арифметических прогрессий имеет вид – 1, 2, 3, 4, 5, 6…. ® ¥.
Я написал предыдущий ряд разностей по принципу личной симпатии. Подстраховался от критики, ежели бы у кого-то не получилось составить систему уравнений, например, с разностью d = 7, ибо для нетренированных рук могут возникнуть трудности.
И ещё. Формулы членов матриц составных чисел (СЧ), которые описываются в системах уравнений двойными суммами. Для этого требуется всего лишь в значения переменных двойных сумм вставить их аналитические выражения через переменные ![]() и
и ![]() - столбцы и строки матриц.
- столбцы и строки матриц.
Тогда формула любого члена матриц СЧ таблицы 4, примет вид (30![]() I - 17) (30
I - 17) (30![]() j - 23).
j - 23).
Аналогично для таблицы 7 - (10![]() I - 3) (10
I - 3) (10![]() j - 7).
j - 7).
Для таблицы 8, ряда нечётных чисел - (2![]() I + 1) (2
I + 1) (2![]() j + 1).
j + 1).
Для таблицы 9, ряда натуральных чисел - (![]() I + 1) (
I + 1) (![]() j + 1).
j + 1).
Заостряю внимание на том факте, что это уже не номера членов СЧ в рядах простых чисел ПЧ + СЧ, а численные значения этих номеров. И подобных уравнений СЧ можно составить по числу систем арифметических прогрессий, и даже значительно больше, т.е. бесконечное множество.
Всё же для наглядности распишу систему уравнений таблицы 3 предыдущей работы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() и
и ![]() - столбцы и строки матриц, индексами не снабжаю.
- столбцы и строки матриц, индексами не снабжаю.
И уж больно симпатичная система из 2-х уравнений с разностью арифметических прогрессий d=6.
| 5х5 | 7х7 | 5х11 | 5х17 | 7х13 | ||||||||||||
| 1 | 7 | 13 | 19 | 25 | 31 | 37 | 43 | 49 | 55 | 61 | 67 | 73 | 79 | 85 | 91 | 97 |
| 5х7 | 5х13 | 7х11 | 5х19 | |||||||||||||
| 5 | 11 | 17 | 23 | 29 | 35 | 41 | 47 | 53 | 59 | 65 | 71 | 77 | 83 | 89 | 95 | 101 |
Напишу только формулы составных чисел
1 – для верхнего ряда (6![]() I - 1) (6
I - 1) (6![]() j - 1), (6
j - 1), (6![]() k + 1) (6
k + 1) (6![]() e +1).
e +1).
2 – для нижнего ряда (6![]() I + 1) (6
I + 1) (6![]() j - 1).
j - 1).
А написал с единственной целью сравнить формулы разных систем простых чисел.
В системе c d = 30 число 91 – это (30![]() - 17) (30
- 17) (30![]() - 23), при
- 23), при ![]() = 1,
= 1, ![]() = 1.
= 1.
В системе c d = 10 это же число – (10![]() - 3) (10
- 3) (10![]() - 7), при
- 7), при ![]() = 2,
= 2, ![]() = 1.
= 1.
В системе c d = 6 ……………… – (6![]() + 1) (6
+ 1) (6![]() + 1), при
+ 1), при ![]() = 1,
= 1, ![]() = 2.
= 2.
В системе c d = 4 ……………… – (4![]() - 1) (4
- 1) (4![]() + 1), при
+ 1), при ![]() = 2,
= 2, ![]() = 3.
= 3.
В системе c d = 2 ……………… – (2![]() + 1) (2
+ 1) (2![]() + 1), при
+ 1), при ![]() = 3,
= 3, ![]() = 6.
= 6.
В системе c d = 1 ……………… – (![]() + 1) (
+ 1) (![]() +1), при
+1), при ![]() = 6,
= 6, ![]() = 12.
= 12.
|
|
| 11 |
| 16 |
| 21 |
| 26 |
|
|
+7 |
+13 |
+19 |
+25 |
+31 | |||||
| 13 |
| 24 |
| 35 |
| 46 |
| 57 | … |
|
|
+13 |
+19 | |||||||
| 20 | +17
| 37 |
| 54 | 71 | 88 | … | ||
|
|
+1 | ||||||||
| 27 |
| 50 |
| 73 | 96 | 119 | … | ||
|
+7 |
| ||||||||
| 34 |
| 63 |
| 92 | 121 | 150 | … | ||
| … | … | … | … | … |
| 9 |
| 16 |
| 23 |
| 30 |
| 37 |
|
|
+7 |
+13 |
+19 |
+25 |
+31 | |||||
| 16 |
| 29 |
| 42 |
| 55 |
| 68 | … |
|
|
+11 | ||||||||
| 27 | +19
| 42 | 61 | 80 | 99 | … | |||
|
|
+11 | ||||||||
| 30 |
| 55 | 80 | 105 | 130 | … | |||
|
+7 |
| ||||||||
| 37 |
| 68 | 99 | 130 | 161 | … | |||
| … | … | … | … | … |
 | |||
| |||
Похожие работы
... ряда нечётных чисел - (2I + 1) (2 j + 1). Для таблицы 9, ряда натуральных чисел - (I + 1) ( j + 1). Заостряю внимание на том факте, что это уже не номера членов СЧ в рядах простых чисел ПЧ + СЧ, а численные значения этих номеров. И подобных уравнений СЧ можно составить по числу систем арифметических прогрессий, и даже значительно больше, т.е. бесконечное множество. Всё же для наглядности распишу ...
... либо простым, либо произведением нескольких простых чисел. Но они не умели этого доказывать. Пифагор или кто-то из его последователей нашел доказательство этого утверждения. Теперь легко объяснить роль простых чисел в математике: они являются теми кирпичиками, из которых с помощью умножения строят все остальные числа. Хорошо было бы, если все простые числа можно было сосчитать! Пусть их было бы ...
... что предмету не присуще некоторое свойство. Объединенная классификация простых категорических суждений по количеству и качеству. В каждом суждении имеется количественная и качественная характеристика. Поэтому в логике применяется объединенная классификация суждений по количеству и качеству, на основе которой выделяются следующие 4 типа суждений: 1. суждение А общеутвердительное. Его ...
... первичного и бухгалтерского учета. Первичный учет – регистрация фактов по мере их возникновения. Различают отчетность: - Общегосударственная отчетность собирается органами общегосударственной статистики по всем хозяйственным структурам не зависимо от формы их собственности и отраслевой принадлежности; - Ведомственная отчетность собирается для нужд управления в рамках министерств или ...

0 комментариев