Белотелов В.А.
Нижегородская обл.
г. Заволжье
Дополнение к предыдущей работе «Закономерность распределения простых чисел в ряду натуральных чисел» размещённой на сайте:
http://www.referat.ru/pub/item/28291
Там где даны в качестве примера разности арифметических прогрессий и указан их ряд 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60. На самом деле пропусков в ряду быть не должно. Ряд разностей арифметических прогрессий имеет вид – 1, 2, 3, 4, 5, 6….® ¥.
Я написал предыдущий ряд разностей по принципу личной симпатии. Подстраховался от критики, ежели бы у кого-то не получилось составить систему уравнений, например, с разностью d = 7, ибо для нетренированных рук могут возникнуть трудности.
И ещё. Формулы членов матриц составных чисел (СЧ), которые описываются в системах уравнений двойными суммами. Для этого требуется всего лишь в значения переменных двойных сумм вставить их аналитические выражения через переменные 
и 
- столбцы и строки матриц.
Тогда формула любого члена матриц СЧ таблицы 4, примет вид (30I - 17) (30j - 23).
Аналогично для таблицы 7- (10I - 3) (10 j - 7).
Для таблицы 8, ряда нечётных чисел - (2I + 1) (2 j + 1).
Для таблицы 9, ряда натуральных чисел - (I + 1) ( j + 1).
Заостряю внимание на том факте, что это уже не номера членов СЧ в рядах простых чисел ПЧ + СЧ, а численные значения этих номеров. И подобных уравнений СЧ можно составить по числу систем арифметических прогрессий, и даже значительно больше, т.е. бесконечное множество.
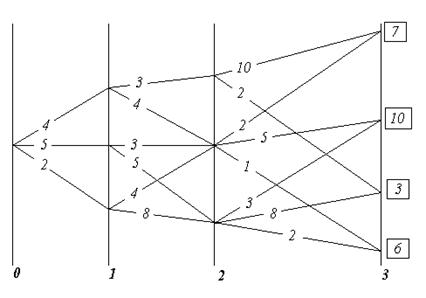
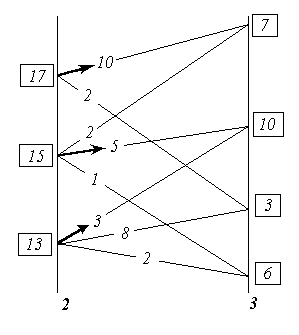
Всё же для наглядности распишу систему уравнений таблицы 3 предыдущей работы.
и - столбцы и строки матриц, индексами не снабжаю.
И уж больно симпатичная система из 2-х уравнений с разностью арифметических прогрессий d=6.
| 5х5 | 7х7 | 5х11 | 5х17 | 7х13 | ||||||||||||
| 1 | 7 | 13 | 19 | 25 | 31 | 37 | 43 | 49 | 55 | 61 | 67 | 73 | 79 | 85 | 91 | 97 |
| 5х7 | 5х13 | 7х11 | 5х19 | |||||||||||||
| 5 | 11 | 17 | 23 | 29 | 35 | 41 | 47 | 53 | 59 | 65 | 71 | 77 | 83 | 89 | 95 | 101 |
Напишу только формулы составных чисел
1 – для верхнего ряда (6I - 1) (6 j - 1), (6k + 1) (6e +1).
2 – для нижнего ряда (6I + 1) (6 j - 1).
А написал с единственной целью сравнить формулы разных систем простых чисел.
В системе c d = 30 число 91 – это (30- 17) (30- 23), при = 1, = 1.
В системе c d = 10 это же число – (10- 3) (10- 7), при = 2, = 1.
В системе c d = 6 ……………… – (6+ 1) (6+ 1), при = 1, = 2.
В системе c d = 4 ……………… – (4- 1) (4+ 1), при = 2, = 3.
В системе c d = 2 ……………… – (2+ 1) (2+ 1), при = 3, = 6.
В системе c d = 1 ……………… – (+ 1) (+1), при = 6, =
Похожие работы
... 25 +29 54 83 112 141 … … … … … … Закономерность распределения простых чисел (дополнение). Белотелов В.А. Нижегородская обл. г. Заволжье vbelotelov@mail. ru Там где даны в качестве примера разности арифметических прогрессий и указан их ряд 1, 2, 4, 6, 10, 12, 18, 20, 30, 36, 60. На самом деле ...
... ли окончить школу, обладая требуемой для аттестата зрелости математической культурой и не научившись в то же время писать совершенно безошибочно. Заканчивая эту главу, посвященную вопросам воспитательного воздействия уроков математики на культуру мышления учащихся, я предвижу естественное и законное недоумение читателя по поводу того, что мною нигде даже не затронута проблема развития элементов ...
... -функция непрерывна. Ввиду произвольности s0 ζ(s) непрерывна на всей области определения. Теперь почленным дифференцированием ряда (1), пока формально, найдём производную дзета-функции Римана: (2). Чтобы оправдать этот результат, достаточно удостовериться в том, что ряд (2) равномерно сходится на промежутке и воспользоваться теоремой о ...
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
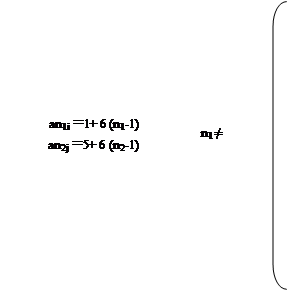
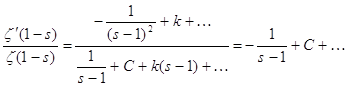
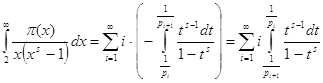
0 комментариев