Навигация
3. Общая топология
Особое место среди областей топологии занимает общая топология. В настоящее время общая топология достигла того наиболее естественного уровня общности, который позволяет излагать топологические принципы, концепции и конструкции с наибольшей прозрачностью и одновременно обеспечить им максимально широкую приложимость в других разделах математики.
Общая топология – это область математики, в которой изучаются общие геометрические свойства, сохраняющиеся при непрерывных и взаимно однозначных отображениях.
Наряду с алгеброй общая Топология составляет основу современного теоретико-множественного метода в математике.
Аксиоматически определяемыми объектами изучения общей топологии являются пространства и их непрерывные отображения. Под топологическим пространством понимается множество объектов произвольной природы, называемых точками, в котором выделена некоторая система подмножеств, называемых открытыми множествами пространства. Эта система должна включать в себя всё пространство и пустое множество и содержать в себе вместе с любыми двумя множествами их пересечение и вместе с любым набором множеств множество, которое является их объединением.
Существенное влияние на развитие общей топологии оказало введённое П.С. Александровым понятие бикомпактности. Александров и Урысон создали теорию бикомпактных пространств. Бикомпактные пространства – один из главных объектов исследования в общей топологии – и в настоящее время находятся в центре внимания математиков. Они играют важную роль в теории размерности, теории гомологий и других разделах топологии, а также имеют основное значение в функциональном анализе. Всякое вполне регулярное пространство является подмножеством некоторого бикомпактного хаусдорфова пространства.
В настоящее время наиболее распространённым является следующее определение бикомпактного пространства: пространство называется бикомпактным, если из всякого открытого покрытия этого пространства можно выбрать конечное число покрывающих множеств.
В литературе можно встретить и другие классы пространств, родственные бикомпактным, например псевдокомпактные, квазикомпактные. Бикомпактные пространства занимают главное место среди них и играют такую же роль в общей топологии, как компакты в классе метризуемых пространств.
Кроме того общая топология посвящена изучению понятий непрерывности, а также других понятий, таких как компактность или отделимость, как таковых, без обращения к другим инструментам.
4. Топологическое пространство
Топологическое пространство – основной объект изучения топологии. Понятие топологического пространства можно рассматривать как обобщение понятия геометрической фигуры, в котором мы отвлекаемся от свойств наподобие размера или точного положения частей фигуры в пространстве, и сосредотачиваемся только на взаимном расположении частей. Топологические пространства возникают естественно почти во всех разделах математики.
Итак, топологическое пространство определяется через систему открытых множеств посредством аксиом. Естественно, само это понятие базируется на предварительных общих понятиях «пространство» и «открытое множество».
В современной математике пространство определяют как некоторое абстрактное множество произвольных объектов, для которых задана определённая операция, осуществляющая известное отношение между элементами пространства. Базой для построения теории того или иного абстрактного пространства является, с одной стороны, общематематическое понятие множества, под которым понимается произвольная совокупность любых объектов (элементов), а с другой, – установленные определённым образом структурные отношения между этими объектами.
Пусть дано множество X. Множество T его подмножеств называется топологией на X, если выполнены следующие свойства:
- Все X и пустое множество принадлежат T,
- Объединение произвольного семейства множеств, принадлежащих T, принадлежит T,
- Пересечение двух множеств, принадлежащих T, принадлежит T.
Множество X вместе с заданной на нем топологией T называется топологическим пространством. Подмножества X, принадлежащие T, называются открытыми множествами.
Потребность в развитии общего подхода к понятию пространства возникла довольно давно – в конце прошлого и начале нынешнего столетия. В связи с развитием теории функций действительного переменного и функционального анализа возникли и другие объекты – функциональные пространства и их подмножества, – для исследования которых также требуются понятия и методы общей топологии.
В настоящее время топологические методы исследования применяются не только в анализе, но и во многих других отраслях математики. Значительной является роль топологических методов в дифференциальных уравнениях. В результате синтеза идей общей топологии и функционального анализа возникла теория топологических векторных пространств. Абстрактные топологические пространства неожиданным образом могут возникать и применяться в самых различных областях математики.
Общепринятое ныне понятие топологического пространства возникло не сразу. Появившееся ранее метрические пространства, которые и по сей день являются важным предметом изучения общей топологии, не могли удовлетворить математиков.
Первые достаточно общие определения топологического пространства даны в работах Фреше, Рисса и Хаусдорфа. Окончательно определение топологического пространства было сформулировано польским математиком К. Куратовским и П.С. Александровым.
5. Важные проблемы и результаты
Теорема Жордана о замкнутой кривой. Если на поверхности проведена простая замкнутая кривая, то существует ли какое-либо свойство кривой, которое сохраняется при деформации поверхности? Существование такого свойства вытекает из следующей теоремы: простая замкнутая кривая на плоскости делит плоскость на две области, внутреннюю и внешнюю. Эта кажущаяся тривиальной теорема очевидна для кривых простого вида, например, для окружности; однако для сложных замкнутых ломаных дело обстоит иначе. Теорема была впервые сформулирована и доказана К. Жорданом (1838–1922); однако доказательство Жордана оказалось ошибочным. Удовлетворительное доказательство было предложено О. Вебленом (1880–1960) в 1905.
Теорема Брауэра о неподвижной точке. Пусть D – замкнутая область, состоящая из окружности и ее внутренности. Теорема Брауэра утверждает, что для любого непрерывного преобразования, переводящего каждую точку области D в точку этой же области, существует некоторая точка, которая остается неподвижной при этом преобразовании. (Преобразование не предполагается взаимно однозначным.) Теорема Брауэра о неподвижной точке представляет особый интерес потому, что она, по-видимому, является, наиболее часто используемой в других разделах математики топологической теоремой.
Проблема четырех красок. Проблема заключается в следующем: можно ли любую карту раскрасить в четыре цвета так, чтобы любые две страны, имеющие общую границу, были раскрашены в различные цвета? Проблема четырех красок топологическая, так как ни форма стран, ни конфигурация границ не имеют значения.
Гипотеза о том, что четырех красок достаточно для соответствующей раскраски любой карты, была впервые высказана в 1852. Опыт показал, что четырех красок действительно достаточно, но строгого математического доказательства не удавалось получить на протяжении более ста лет. И только в 1976 К. Аппель и В. Хакен из Иллинойского университета, затратив более 1000 часов компьютерного времени, добились успеха.
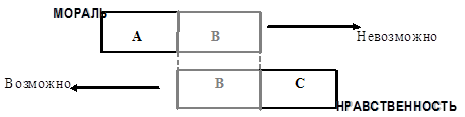
Односторонние поверхности. Простейшей односторонней поверхностью является лист Мёбиуса, названный так в честь А. Мёбиуса, открывшего его необычайные топологические свойства в 1858. Пусть ABCD (рис. 2, а) – прямоугольная полоска бумаги. Если склеить точку A с точкой B, а точку C с точкой D (рис. 2, б), то получится кольцо с внутренней поверхностью, наружной поверхностью и двумя краями. Одну сторону кольца (рис. 2, б) можно окрасить. Окрашенная поверхность будет ограничена краями кольца. Жук может совершить «кругосветное путешествие» по кольцу, оставаясь либо на окрашенной, либо на неокрашенной поверхности. Но если полоску перед склеиванием концов перекрутить на пол-оборота и склеить точку A с точкой C, а B с D, то получится лист Мёбиуса (рис. 2, в). У этой фигуры есть только одна поверхность и один край. Любая попытка окрасить только одну сторону листа Мёбиуса обречена на неудачу, так как у листа Мёбиуса всего одна сторона. Жук, ползущий по середине листа Мёбиуса (не пересекая края), вернется в исходную точку в положении «вверх ногами». При разрезании листа Мёбиуса по средней линии он не распадается на две части.
Узлы. Узел можно представлять себе как запутанный кусок тонкой веревки с соединенными концами, расположенный в пространстве. Простейший пример – из куска веревки сделать петлю, пропустить один из ее концов сквозь петлю и соединить концы. В результате мы получим замкнутую кривую, которая остается топологически той же самой, как бы ее ни растягивать или скручивать, не разрывая и не склеивая при этом отдельные точки. Проблема классификации узлов по системе топологических инвариантов пока не решена.
Заключение
Топология – очень красивая наука. Она осуществляет связь геометрии с алгеброй. Ее идеи и образы играют ключевую роль практически во всей современной математике – в дифференциальных уравнениях, механике, комплексном анализе, алгебраической геометрии, функциональном анализе, математической и квантовой физике, теории представлений, и даже – в удивительно преображенном виде – в теории чисел, комбинаторике и теории сложности вычислений. В частности, современная топология находит широкое применение в механике и математической физике. Топологические методы широко используются в качественной теории движения твердого тела.
Список использованных источников и литературы
1. Александров П.С., Пасынков Б.А. Введение в теорию размерности. М.: Наука, 1973
2. Годеман Р. Алгебраическая топология и теория пучков. М.: ИЛ, 1961
3. Келли Дж.Л. Общая топология. М.: Наука 1968
4. Телеман К. Элементы топологии и дифференцируемые многообразия. М.: Мир, 1967
5. Хирцебрух Ф. Топологические методы в алгебраической геометрии. М.: Мир, 1973
6. Стюарт Я. Топология // Квант – 1992. – №7.
Похожие работы
... итог сказанному выше, можно утвердительно сказать о том, что поступление названных учебников «Моя математика» в школы даст возможность учителям начального звена обучения более системно и продуктивней осуществлять развитие пространственных представлений младших школьников. Заключение Из курсов педагогики и методики математики известно, что деятельность может быть репродуктивной и продуктивной. ...
... обменом в них в принципе не может быть гарантированно быстрым. В глобальных сетях гораздо важнее не качество связи, а сам факт ее существования. Нередко выделяют еще один класс компьютерных сетей - городские сети (MAN, Metropolitan Area Network), которые обычно бывают ближе к глобальным сетям, хотя иногда имеют некоторые черты локальных сетей - например, высококачественные каналы связи и ...
... «хождение по мукам» у школы закончатся. ШИТТ до ноября 2004 г. функционировала при детском фонде им. Мирзо Турсун-Заде «Ошёни баланд» в соответствии с его уставом. С 29 ноября 2004 г. «Школа информационных и телекоммуникационных технологий -ШИТТ» и ее устав были зарегистрированы Министерством юстиции Республики Таджикистан (рег. № 001-1455, номер удостоверения Ва № 0007038 ) как внешкольную и ...
... , но и сами «правила игры», делающей такое положение вещей возможным. Он характеризует социальную сторону самого общения как важнейшего источника духовной жизни общества. Другими словами, имидж отражает саму необходимость согласования жизни психики, вплоть до самых интимных ее сторон, с индивидуальным и групповым опытом бытия социальной и политической в л а с т и. Резонность такого подхода ...



0 комментариев