Навигация
1. Необходимость.
Пусть a - корень многочлена f(x), тогда по следствию 2 f(x) делится на (x-a) без остатка.
Таким образом делимость f(x) на (x-a) является необходимым условием для того, чтобы a являлось корнем f(x), т.к. является следствием из этого.
2. Достаточность.
Пусть многочлен f(x) делится без остатка на (x-a),
тогда R=0, где R - остаток от деления f(x) на (x-a), но по теореме Безу R=f(a), откуда выходит, что f(a)=0, а это означает, что a является корнем f(x).
Таким образом, делимость f(x) на (x-a) является и достаточным условием для того, чтобы a являлось корнем f(x).
Делимость f(x) на (x-a) является необходимым и достаточным условием для того, чтобы a являлось корнем f(x), что и требовалось доказать.
Следствие 7:
Многочлен, не имеющий действительных корней, в разложении на множители линейных множителей не содержит.
Доказательство:
Воспользуемся методом от противного: предположим, что не имеющий корней многочлен f(x) при разложении на множители содержит линейный множитель
(x–a):
f(x)=(x–a)q(x),
тогда бы он делился на (x–a), но по следствию 6 a являлось бы корнем f(x), а по условию он действительных корней не содержит. Мы пришли к противоречию, значит наше предположение неверно и многочлен, не имеющий действительных корней, в разложении на множители линейных множителей не содержит, что и требовалось доказать.
Применение теоремы
Остановлюсь на рассмотрении некоторых примеров применения теоремы Безу к решению практических задач.
Следует отметить, что при решении уравнений с помощью теоремы Безу необходимо:
· найти все целые делители свободного члена;
· из этих делителей найти хотя бы один корень уравнения (a);
· левую часть уравнения разделить на (x-a);
· записать в левой части уравнения произведение делителя и частного;
· решить полученное уравнение.
Пример 1
Найти остаток от деления многочлена x3–3x2+6x–5на двучлен x–2.
По теореме Безу:
R=f(2)=23–3*22+6*2–5=3.
Ответ: R=3.
Пример 2
При каком значении a многочлен x4+ax3+3x2–4x–4 делится без остатка на двучлен x–2?
По теореме Безу: R=f(2)=16+8a+12–8– 4=8a+16.
Но по условию R=0, значит 8a+16=0, отсюда a=-2.
Ответ: a=-2.
Пример 3
При каких значениях a и b многочлен ax3+bx2–73x+102 делится на трёхчлен x2–5x+6 без остатка?
Разложим делитель на множители: x2–5x+6=(x–2)(x–3).
Поскольку двучлены x–2 и x–3 взаимно просты, то данный многочлен делится на x–2 и на x–3, а это значит, что по теореме Безу:
R1=f(2)=8a+4b–146+102=8a+4b–44=0
R2=f(3)=27a+9b–219+102=27a+9b-117=0
![]() Решу систему уравнений:
Решу систему уравнений:
8a+4b–44=0 2a+b=11
27a+9b–117=0 3a+b=13
Отсюда получаем: a=2, b=7.
Ответ: a=2, b=7.
Пример 4.
При каких значениях a и b многочлен x4+ax3–9x2+11x+b
делится без остатка на трёхчлен x2–2x+1?
Представим делитель так: x2 – 2x + 1 = (x – 1)2
Данный многочлен делится на x–1 без остатка, если по теореме Безу:
R1=f(1)=1+a–9+11+b=a+b+3=0.
Найдём частное от деления этого многочлена на x–1:
![]() _ x4+ax3–9x2+11x–a–3 x–1
_ x4+ax3–9x2+11x–a–3 x–1
![]() x4–x3 x3+(a+1)x2+(a–8)x+(a+3)
x4–x3 x3+(a+1)x2+(a–8)x+(a+3)
_(a+1)x3–9x2
![]() (a+1)x3–(a + 1)x2
(a+1)x3–(a + 1)x2
_(a–8)x2+11x
![]()
![]()
![]()
![]() (a–8)x2–(a–8)x
(a–8)x2–(a–8)x
_(a+3)x–a–3
![]()
![]()
![]()
![]()
![]()
![]()
![]() (a+3)x–a–3
(a+3)x–a–3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0
0
Частное x3+(a+1)x2+(a–8)x+(a+3) делится на (x–1) без остатка, откуда
R2=f(1)=1+(a+1)*1+(a–8)*1+a+3=3a–3=0.
Решу систему уравнений:
![]()
![]() a + b + 3 = 0 a + b =-3
a + b + 3 = 0 a + b =-3
3a – 3 = 0 a = 1
Из системы: a=1, b=-4
Ответ: a=1, b=-4.
Пример 5
Разложить на множители многочлен f(x)=x4+4x2–5.
Среди делителей свободного члена число 1 является корнем данного многочлена f(x), а это значит, что по следствию 2 из теоремы Безу f(x) делится на (x–1) без остатка:
f(x)/(x–1)=x3+x2+5x+5, значит f(x)=(x–1)(x3+x2+5x+5).
Среди делителей свободного члена многочлена x3+x2+5x+5 x=-1 является его корнем, а это значит, что по следствию 2 из теоремы Безу x3+x2+5x+5 делится на (x+1) без остатка:
_x4+4x2–5 x–1 _x3+x2+5x+5 x+1
x4–x3 x3+x2+5x+5 x3+x2 x2 +5
_x3+4x2 _5x+5
![]() x3–x2 5x+5
x3–x2 5x+5
_5x2–5 0
![]() 5x2–5x
5x2–5x
![]()
![]()
![]()
![]() _5x–5
_5x–5
5x–5
0
![]() (x3+x2+5x+5)/(x+1)=x2+5, значит x3+x2+5x+5=(x+1)(x2+5).
(x3+x2+5x+5)/(x+1)=x2+5, значит x3+x2+5x+5=(x+1)(x2+5).
Отсюда f(x)=(x–1)(x+1)(x2+5).
По следствию 7 (x2+5) на множители не раскладывается, т.к. действительных корней не имеет, поэтому f(x) далее на множители не раскладывается.
Ответ: x4+4x2–5=(x–1)(x+1)(x2+5).
Пример 6
Разложить на множители многочлен f(x)=x4+324.
f(x) корней не имеет, т.к. x4 не может быть равен -324, значит, по следствию 7 f(x) на множители не раскладывается.
Ответ: многочлен на множители не раскладывается.
Пример 7
Составить кубический многочлен, имеющий корень 4 кратности 2 и корень -2.
По следствию 3, если многочлен f(x) имеет корень 4 кратности 2 и корень -2, то он делится без остатка на (x–4)2(x+2), значит:
f(x)/(x–4)2(x+2)=q(x), т.е.
f(x)=(x–4)2(x+2)q(x),
f(x)=(x2–8x+16)(x+2)q(x),
f(x)=(x3–8x2+16x+2x2–16x+32)q(x),
f(x)=(x3–6x2+32)q(x).
(x3–6x2+32) - кубический многочлен, но по условию f(x) – также кубический многочлен, следовательно, Q(x) – некоторое действительное число. Пусть Q(x)=1, тогда f(x)=x3–6x2+32.
Ответ: x3–6x2+32.
Пример 8
Решить уравнение x4+3x3-13x2-9x+30=0.
30![]()
![]() 1;
1; ![]() 2,
2, ![]() 3,
3, ![]() 5,
5, ![]() 6,
6, ![]() 10.
10.
(x-2)(x3+5x2-3x-15)=0
(x-2)(x+5)(x2-3)=0
_x4+3x3-13x2-9x+30 x-2
x4-2x3 x3+5x2-3x-15
_5x3-13x2
5x3-10x2
_-3x2-9x
-3x2+6x
_-15x+30
-15x+30
0
Ответ: x1=2,x2=-5,x3,4=![]() .
.
Пример 9
Решить уравнение x6+x5-7x4-5x3+16x2+6x-12=0.
Посмотрев на уравнение, сразу можно сказать, что по следствию 4 оно имеет не более 6 корней уравнения.
-12![]()
![]() 1;
1; ![]() 2;
2; ![]() 3;
3; ![]() 4;
4; ![]() 6;
6; ![]() 12.
12.
_x6+x5-7x4-5x3+16x2+6x-12 x-1
x6-x5 x5+2x4-5x3-10x2+6x+12
_2x5-7x4
2x5-7x4
_-5x4-5x3
-5x4+5x3
_-10x3+16x2 _x5+2x4-5x3-10x2+6x+12 x+2
-10x3-10x2 x5+2x4 x4-5x2+6
_6x2+6x _-5x3-10x2
6x2-6x -5x3-10x2
_12x-12 _6x+12
12x-12 6x+12
0 0
x6+x5-7x4-5x3+16x2+6x-12=(x-1)(x5+2x4-5x3-10x2+6x+12)=0
x6+x5-7x4-5x3+16x2+6x-12=(x-1)(x+2)(x4-5x2+6)=0
x4-5x2+6=0 – биквадратное уравнение, x1,2=![]()
![]() , x3,4=
, x3,4=![]()
![]() .
.
Ответ: x1,2=![]()
![]() , x3,4=
, x3,4=![]()
![]() , x5=1,x6=-2.
, x5=1,x6=-2.
Пример 10
Решить уравнение x3-5x2+8x-6=0.
-6![]()
![]() 1;
1; ![]() 2;
2; ![]() 3;
3; ![]() 6.
6.
_x3-5x2+8x-6 x-3
x3-3x2 x2-2x+2
_-2x2+8x
-2x2+6x
_2x-6
2x-6
0
x3-5x2+8x-6=(x2-2x+2)(x-3)=0
x2-2x+2=0 – квадратное уравнение, корней не имеет, т.к. D<0.
Ответ: x=3.
Пример 11
Решить уравнение 6x3+11x2-3x-2=0.
-2![]()
![]() 1;
1; ![]() 2.
2.
_6x3+11x2-3x-2 x+2
6x3+12x2 6x2-x-1
_-x2-3x
-x2-2x
_-x-2
-x-2
0
6x3+11x2-3x-2=(6x2-x-1)(x+2)=0
6x2-x-1=0 – квадратное уравнение, x1=½, x2=-⅓.
Ответ: x1=½, x2=-⅓, x3=-2.
Заключение
Теорема Безу - одна из основных теорем алгебры, названная именем французского ученого Этьена Безу.
Существует несколько следствий из теоремы, которые помогают при решении практических задач. Из рассмотренных примеров можно сделать вывод, что теорема Безу находит применение при решении задач, связанных с делимостью многочленов, например, нахождение остатка при делении многочленов, определение кратности многочленов и т.д. Также, теорема работает при разложении многочленов на множители, при определении кратности корней и многих других.
Теорема Безу находит применение при рассмотрении одной из важнейших задач математики – решении уравнений.
Источники 1. Бородин А.И., Бугай А.С. Биографический словарь деятелей в области математики.
2. Виноградов И.М. (главный редактор) Математическая энциклопедия.
3. Туманов С.И. Элементарная алгебра
4. Яремчук Ф.П., Рудченко П.А. Алгебра и элементарные функции.
5. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварц-бурд С.И. Алгебра и математический анализ.
6. Курош А.Г. Курс высшей алгебры.
7. Internet
Похожие работы
... которого на один ниже степени многочлена Также данный метод называют понижением степени. Благодаря данному способу можно найти оставшиеся корни многочлена. 2.4. Примеры использования теоремы. Пример. Найти остаток от деления многочлена на . Решение. На основании теоремы Безу подставляем вместо x число -5. Получаем r(x)= В результате мы получили остаток r(x) равный 180. Пример. С ...
... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах. § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах. При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...
... решения обязательно выполняется проверка. Не обращается внимание на то, что иррациональные уравнения могут решаться и с использованием понятия равносильности. В данном параграфе представлены различные виды иррациональных уравнений, которые можно отнести к стандартным и решать одним из следующих методов, а именно: 1) метод перехода к уравнению - следствию с последующей проверкой полученных корней ...
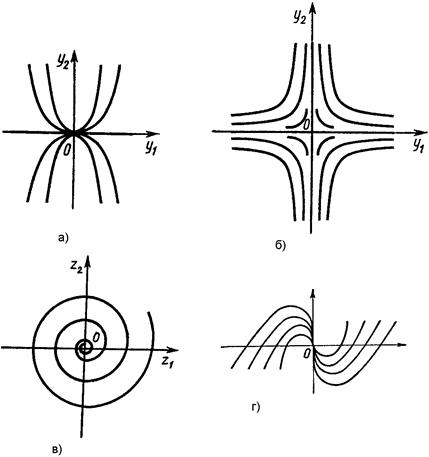
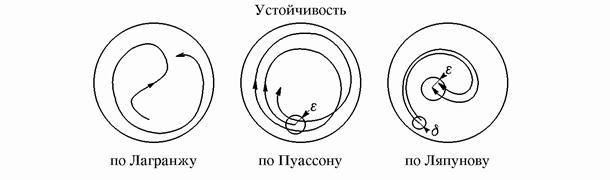
... начальным условиям . Пусть — характеристическое уравнение для определения мультипликаторов. Так как , то оно принимает вид , где . 2. Устойчивость решений систем дифференциальных уравнений. 2.1. Устойчивость по Ляпунову. Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует ...
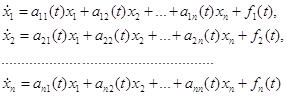
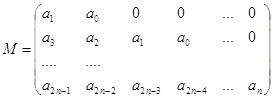
0 комментариев