МОДЕЛЬ СОЛОУ, КАК ПРИМЕР МАКРОЭКОНОМИЧЕСКОЙ ДИНАМИКИ

1.2 МОДЕЛЬ СОЛОУ, КАК ПРИМЕР МАКРОЭКОНОМИЧЕСКОЙ ДИНАМИКИ

Другой тип модели экономического роста представляет модель, предложенная лауреатом Нобелевской премии Р.Солоу. По сравнению с уже рассмотренной моделью роста модель Солоу позволяет более точно описать некоторые особенности макроэкономических процессов. Во-первых, производственная функция в этой модели нелинейна и обладает свойством убывания предельной производительности. Во-вторых, модель учитывает выбытие основного капитала. В-третьих, в модель Солоу включается описание динамики трудовых ресурсов и технического прогресса и их влияние на экономический рост. В-четвертых, здесь ставится и решается задача максимизации уровня потребления на некотором множестве устойчивых траекторий. Все это, конечно, усложняет структуру модели, и получение точных формул для траекторий изменения основных ее показателей становится существенно более сложной задачей. По­этому некоторые другие аспекты описываются в базовой модели Солоу упрощенно: например, считаются постоянными норма сбере­жений и норма выбытия капитала, инвестиционные лаги отсутствуют, а производственная функция имеет постоянную отдачу от масштаба. Кроме того, на начальном уровне анализа модели ищутся не траектории изменения всех ее показателей (как в модели Харрода-Домара), а характеристики состояний устойчивого равновесия, к которым система выходит в долгосрочном периоде. С формальной точки зрения это представляет собой существенно более простую задачу.

Мы не ставим здесь задачу подробно излагать модель Солоу, сформулируем лишь основные ее предпосылки, обозначения и вы­воды.

Предпосылки и обозначения модели Солоу:

·        Производственная функция имеет вид Y= F(K,L) (Y – выпуск или доход, К- капитал, L – труд). Отдача от масштаба постоянна :

F(zK, zL) = zF(K,L). Предельная производительность факторов положительна, но убывает:

Y>0; Y>0; Y<0 ; Y<0 ;

·        Величина выбытия капитала W пропорциональна его величине K: W=δ·K,

где δ – норма выбытия;

·        норма сбережений (инвестиций) α постоянна, и инвестиции I равны α Y;

·        доход Y распределяется на потребление и инвестиции Y=C+1

·        численность занятых L растет с постоянным темпом n;

·        трудосберегающий технический прогресс имеет темп g , то есть число единиц труда с постоянной эффективностью в расчете на одного работающего растет с темпом g

 При сделанных предпосылках производственную функцию можно

рассматривать как зависимость производительности труда  от

его капиталовооруженности  :y =F(k) (здесь L- число единиц труда с постоянной эффективностью (то есть численность занятых при отсутствии трудосберегающего технического прогресса, либо численность условных работников с одинаковой эффективностью - при его наличии). Это вытекает из того, что Y=F(K,L) =L·F(.

Инвестиции приводят к росту капиталовооруженности, а выбытие капитала, рост численности работающих и числа единиц труда с постоянной эффективностью - к ее снижению. Прирост капиталовооруженности k. в результате инвестиций равен i = . Темп снижения капиталовооруженности за счет остальных факторов равен (δ+n+g) (в точности равен, если У,К,L - непрерывные функции времени, и приближенно равен в дискретном случае при малых δ+n+g). Величина снижения капиталовооруженности за счет этих фак­торов равна (δ+n+g)k.

 Величина k находится в состоянии устойчивого равновесия, если ее прирост за счет инвестиций равен ее уменьшению за счет других факторов. Поскольку Y=С+I, после деления этого тождества на L имеем y= c+I , где у - доход, с - потребление, а i - инвестиции на одну единицу труда с постоянной эффективностью. Следовательно, величина I равна α f(k). Условие стабильности показателя k,, таким образом, записывается как

(δ+n+g)·k* =α·f(k*)

и величина k* называется устойчивым уровнем капиталовооруженности. На рис. 1 показана устойчивость равновесия при k = k*. Это - точка равновесия для показателя k, поскольку в этой точке величина удельного прироста капиталовооруженности равна величине ее удельного сокращения, и показатель k остается неизменным. Это равновесие устойчиво, поскольку при k<k* удельные инвестиции превышают уменьшение капиталовооруженности, и ее величина растет. В случае k< k* , наоборот, удельные инвестиции ниже, чем уменьшение капиталовооруженности, и ее величина падает, пока не достигнет k*. Из рис. 1 можно видеть, что в случае увеличения нормы сбережения а график функции инвестиций пойдет выше и, следовательно пересечет прямую (δ+n+g)k правее. Итак, рост нормы сбережения приводит к увеличению устойчивого уровня капиталовооруженности k*, а, следовательно, и устойчивого уровня дохода на единицу труда y* = f(k*)

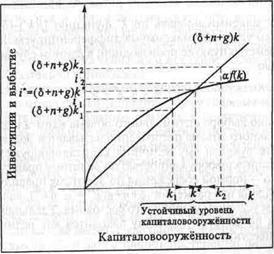
Рис.1

Если численность работающих не растет (или растет медленнее), то есть показатель n равен нулю (или меньше по величине), то прямая (δ+n+g) k имеет меньший наклон и точка k* сдвигается вправо. То же самое происходит при более низком (или нулевом) темпе трудосберегающего технического прогресса g.В устойчивом состоянии темп прироста показателей k,y,c,i равен нулю. Поскольку все это - удельные показатели в расчете на единицу труда с постоянной эффективностью, а эффективность труда одного занятого растет с темпом g, показатели капитала, дохода, потребления и инвестиций в расчете на одного занятого растут с темпом g. При росте численности занятых с темпом n общий объем капитала, дохода, потребления и инвестиций растет в устойчивом состоянии с темпом (n+g). Следовательно, модель Солоу показывает, что единственным источником длительного, устойчивого роста дохода на одного работника, а, следовательно, и душевого потребления, является технический прогресс.

Похожие работы

Моделирование макроэкономических процессов и систем

Скачать

11024

11

2

возможности метода математического моделирования при анализе конкретных социально-экономических процессов достаточно ограничены. В данной курсовой работе будут рассмотрены основные математические модели макроэкономических процессов, такие как мультипликативная производственная функция, кривая Лоренца, различные модели банковских операций, модели межотраслевого баланса Леонтьева, динамическая ...

Инфляция и её влияние на макроэкономические процессы в России

Скачать

141233

0

15

... восстановление может происходить с существенным запаздыванием относительно темпов экономического роста, которое может составлять несколько кварталов. 2.3 Влияние инфляции на макроэкономические процессы Инфляция оказывает сильное влияние на все макроэкономические процессы, происходящие в стране. По мере своего углубления она все более отрицательно воздействует на экономику страны по разным ...

Макроэкономические проблемы и показатели. Совокупный спрос и совокупное предложение

Скачать

62041

8

0

... . При этом мы будем использовать так называемые агрегированные экономические показатели, суммированные показатели объёмов производства, расходов и доходов. Мы их называли макроэкономическими показателями. Анализ модели совокупного спроса и совокупного предложения позволит нам понять механизм формирования уровня цен в экономике в целом, объяснить причины его изменений. Совокупный спрос (AD) - это ...

АРТ-моделирование на фондовом рынке

Скачать

88755

38

45

... рынка выполнение всех необходимых процедур в конечном счете не может гарантировать получение реальной картины динамики доходности. Глава III. АРТ-моделирование: теория и практика   § 1. Эконометрический подход к моделированию фондового рынка: от общего к частному Для выявления экономических взаимосвязей (в частности, зависимостей на фондовом рынке) широко применяется аппарат экономико- ...